
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристические многочлены и собственные числа
|
|
|
|
Инвариантные подпространства. Собственные векторы. Простейшие свойства
Азн.16.1. f ÎEnd(V). Подпространство U пространства V называется инвариантной относительно f (или f - инвариантной), когда 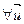 Î U
Î U  Î U (1)
Î U (1)
Прыклад 16.2.1. V =V2, prx – проекция на ось Ox. U 1=R  R} - инвариантная относительно prx подпространство, так как
R} - инвариантная относительно prx подпространство, так как  R,
R,  U 1. U 2=R
U 1. U 2=R 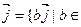 R} - также инвариантные относительно prx подпространство, так как
R} - также инвариантные относительно prx подпространство, так как 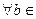 R,
R, 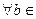 R
R 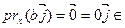 U 2.
U 2. 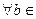 R
R 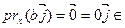 U 2.
U 2.
16.2.2. V = V3, f – поворот вокруг оси Oz на угол  . f - инвариантными являются U z і U xoy - просторо векторов плоскости xOy.
. f - инвариантными являются U z і U xoy - просторо векторов плоскости xOy.
16.2.3. Для оператора D деференцирования пространства P[x] для произвольного натурального n пространства
P n[x] является D-инвариантными.
16.2.4. Для произвольного f ÎEnd(V) подпространства  і V являются f - инвариантными. Они называются тривиальными.
і V являются f - инвариантными. Они называются тривиальными.
Св-во 16.3 Когда f ÎEnd(V), U 1 и U 2 f - инвариантные подпространства, тогда U 1  U 2 также f- инвариантное подпространство. Доказ. Рассмотрим
U 2 также f- инвариантное подпространство. Доказ. Рассмотрим 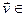 U 1
U 1  U 2 . То
U 2 . То 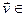 U 1 откуда следует, что
U 1 откуда следует, что 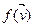 Î U 1. Аналогично,
Î U 1. Аналогично, 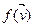 Î U 2, ■
Î U 2, ■
Азн. 16.4. Ненулевой вектор 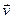 Î V называется собственным вектором оператора f ÎEnd(V), когда существует
Î V называется собственным вектором оператора f ÎEnd(V), когда существует  ÎP такой, что f
ÎP такой, что f  . При этом говорят, что
. При этом говорят, что  - собственная значимость линейного оператора f, которое соответствует вектору
- собственная значимость линейного оператора f, которое соответствует вектору  .
.
Прыклад 16.5. У линейного оператора prx линейного пространства V2 вектор  является собственным из собственной значимостью 1, поскольку
является собственным из собственной значимостью 1, поскольку 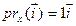 . Т.к.
. Т.к.  , вектор
, вектор  - собственный, которому соответствует собственная значимость 0.
- собственный, которому соответствует собственная значимость 0.
Св-во 16.6. Когда 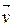 - собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость  ÎP, тогда для произвольного
ÎP, тогда для произвольного 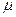 ÎP\{0} вектор
ÎP\{0} вектор 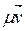 также является собственным вектором оператора f, которому также соответствует собственная значимость
также является собственным вектором оператора f, которому также соответствует собственная значимость  . Доказ. По условию
. Доказ. По условию  . Тогда очевидно, что
. Тогда очевидно, что  і
і 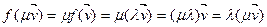 .■
.■
Вынік 16.7 Когда 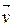 - собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость  , тогда подпространство P
, тогда подпространство P 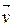 ={
={ 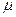
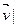
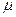 ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость
ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость 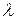 . Доказ. Следует из 17.6 и того, что f
. Доказ. Следует из 17.6 и того, что f 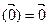 .■
.■
Азн. 16.8 Пусть  (3) -базис пространства V, f ÎEnd(V) і А =
(3) -базис пространства V, f ÎEnd(V) і А = 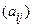 – матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
– матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
 (4).
(4).
Азн. 16.8 Пусть  (3) -базис пространства V, f ÎEnd(V) і А =
(3) -базис пространства V, f ÎEnd(V) і А = 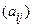 – матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
– матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
 (4).
(4).
Св-во 16.9 Характеристические многочлены сопряжены, матриы равны. Доказ. Пусть 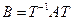

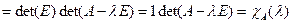 ■
■
Св-во 16.10. Определение 16.8. корректно, т.е. характеристический многочлен эндоморфизма не зависит от того, в каком базисе взята его матрица. Доказательство: Если f ÎEnd(V), в базисе  (1) имеет матрицу А, в
(1) имеет матрицу А, в 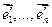 имеет матрицу В и Т – матрица перехода от базиса (1) к новому базису, то
имеет матрицу В и Т – матрица перехода от базиса (1) к новому базису, то 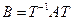 . по 16.9.:
. по 16.9.: 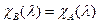 ■
■
Т. 16.11. Скаляр 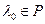 является собственным значением эндоморфизма f ÎEnd(V)
является собственным значением эндоморфизма f ÎEnd(V) 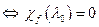 . Доказательство:
. Доказательство:  - собственное значение f.
- собственное значение f.  . Фиксируем какой-нибудь базис (1). В нем f имеет матрицу А, а
. Фиксируем какой-нибудь базис (1). В нем f имеет матрицу А, а  имеет ненулевой столбец координат
имеет ненулевой столбец координат  .
. 
 . Рассмотрим систему
. Рассмотрим систему  . Она однородна и имеет ненулевое решение -
. Она однородна и имеет ненулевое решение -  .
.  . Обратно: пусть
. Обратно: пусть 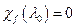 . Фиксируем базис (1). Пусть А – матрица f в этом же базисе. Рвссмотрим систему
. Фиксируем базис (1). Пусть А – матрица f в этом же базисе. Рвссмотрим систему 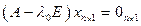 . Она однородна. Ее определитель равен
. Она однородна. Ее определитель равен  , значит система имеет не только нулевое решение. Пусть
, значит система имеет не только нулевое решение. Пусть  - ненулевое решение. Рассмотрим
- ненулевое решение. Рассмотрим  , который в базисе (1) имеет мтолбец координат
, который в базисе (1) имеет мтолбец координат  , тогда
, тогда 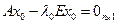 ,
,  Равенство этих столбцов соотв. равенству столбцов координат и равенству векторов.
Равенство этих столбцов соотв. равенству столбцов координат и равенству векторов.  значит
значит  - собственный вектор оператора f, которому соотвествует собственное значение
- собственный вектор оператора f, которому соотвествует собственное значение  . ■
. ■
Следствие 16.12: Пусть dimV=n. f ÎEnd(V) и в базисе (1) имеет матрицу А. Если  - собственное значение f, то оно соответствует векторам
- собственное значение f, то оно соответствует векторам  , столбцы координат которых в базисе (1) являются ненулевым решением системы
, столбцы координат которых в базисе (1) являются ненулевым решением системы 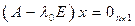 . Доказательство: доказано в 16.11. ■
. Доказательство: доказано в 16.11. ■
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 459; Нарушение авторских прав?; Мы поможем в написании вашей работы!