
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственные числа самосопряженных операторов
|
|
|
|
Лемма 17.6. У любого линейного оператора вещественного пространства есть инвариантное подпространство размерности 1 или 2. Доказательство: 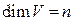 . Фиксируем произвольный базис. Оператор f в нем имеет матрицу
. Фиксируем произвольный базис. Оператор f в нем имеет матрицу 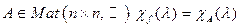 . Рассматриваем этот многочлен как многочлен с комплексными коэффициентами. По основной теореме алгебры этот многочлен имеет корень
. Рассматриваем этот многочлен как многочлен с комплексными коэффициентами. По основной теореме алгебры этот многочлен имеет корень  . Если
. Если 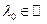 , то он соответствует некоторому
, то он соответствует некоторому  и
и 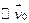 - пространство инвариантно относительно f.
- пространство инвариантно относительно f. 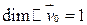 . Пусть
. Пусть 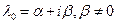 . Рассмотрим систему линейных уравнений над полем комплексных чисел
. Рассмотрим систему линейных уравнений над полем комплексных чисел 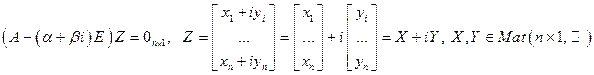
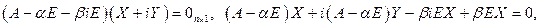
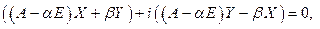 т.к. справа – действительная матрица, то
т.к. справа – действительная матрица, то 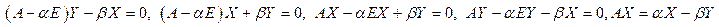
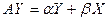 . Рассмотрим векторы
. Рассмотрим векторы  и
и 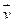 , которые в этом же базисе, где брали матрицу А, имеют столбцы координат Х и Y, тогда АХ и АY – столбцы координат
, которые в этом же базисе, где брали матрицу А, имеют столбцы координат Х и Y, тогда АХ и АY – столбцы координат 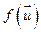 и
и 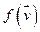 в этом же базисе.
в этом же базисе. 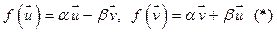 . Рассмотрим линейную оболочку
. Рассмотрим линейную оболочку 
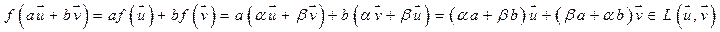
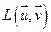 - подпространство инвариантное относительно f.
- подпространство инвариантное относительно f. 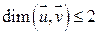 . ■
. ■
Свойство 17.7. Все собственные числа самосопряженного оператора - вещественные. Доказательство. От противоположного. Пусть f собственное число 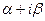 , где
, где 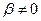 . Из доказательства леммы 17.6 следует,
. Из доказательства леммы 17.6 следует,
что Г ненулевые векторы 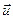 и
и 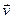 :
: 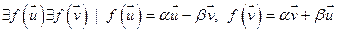 .
. 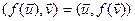 ;
; 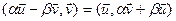 ;
; 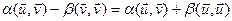 ;
;  . Но
. Но 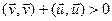 , получили противоречие. n
, получили противоречие. n
Теорема 17.8. f – самосопряженный оператор 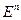 , тогда существует ортонормированный базис
, тогда существует ортонормированный базис 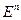 из собственных векторов f. Доказательство: ММИ по n. Если n=1, верно, т.к. любое линейное преобразование одномерного пространства
из собственных векторов f. Доказательство: ММИ по n. Если n=1, верно, т.к. любое линейное преобразование одномерного пространства 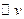 есть умножение на скаляр. Пусть верно для n+1.
есть умножение на скаляр. Пусть верно для n+1. 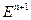 . Возьмем произвольное собственное значение
. Возьмем произвольное собственное значение  , которое соответствует
, которое соответствует 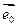 .
. 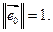 Известно, что
Известно, что  - одномерное собственное пространство f. Рассмотрим
- одномерное собственное пространство f. Рассмотрим 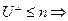 по посылке индукции.
по посылке индукции. 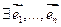 - ортонормированный базис из собственных векторов f. Покажем, что
- ортонормированный базис из собственных векторов f. Покажем, что 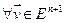 разлагается в сумму векторов
разлагается в сумму векторов 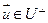 и вектора
и вектора 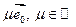 .
. 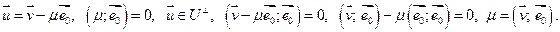
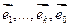 - базис
- базис 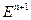 . Покажем это:
. Покажем это: 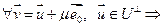 разлагается по базису
разлагается по базису 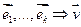 разлагается по
разлагается по 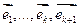 . Значит система линейно независима и она является ортонормированным базисом из собственных векторов f. n
. Значит система линейно независима и она является ортонормированным базисом из собственных векторов f. n
Св-во 17.9. Для любой симметричной матрицы А существует ортогональная матрица Т такая, что 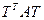 - диагональная. Доказательство: Пусть
- диагональная. Доказательство: Пусть 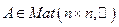 . Рассмотрим
. Рассмотрим 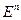 . Фиксируем в нем
. Фиксируем в нем 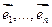 . Рассмотрим оператор f, который в этом базисе имеет матрицу А. Базис ортонормированный. Матрица симметричная, значит линейный оператор самосопряжен (по 17.4.). По 17.8. существует ортонормированный базис
. Рассмотрим оператор f, который в этом базисе имеет матрицу А. Базис ортонормированный. Матрица симметричная, значит линейный оператор самосопряжен (по 17.4.). По 17.8. существует ортонормированный базис 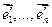 из собствееных векторов оператора f, в котором оператор f имеет матрицу
из собствееных векторов оператора f, в котором оператор f имеет матрицу 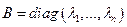 . Возьмем матрицу Т перехода от исходного базиса к базису из собственных векторов. Т.к. оба базиса ортонормированных, то Т – ортагональная.
. Возьмем матрицу Т перехода от исходного базиса к базису из собственных векторов. Т.к. оба базиса ортонормированных, то Т – ортагональная. 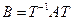 n
n
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 572; Нарушение авторских прав?; Мы поможем в написании вашей работы!