Рівняння руху

Основні рівняння механіки суцільних середовищ

Система рівнянь, яка описує напружений стан і деформацію суцільних середовищ, включає фундаментальні рівняння руху, неперервності енергії, а також рівняння реології і стану. Фундаментальні рівняння базуються на законах ньютонівської механіки і є необхідними, а рівняння реології і стану замикають їх і утворюють необхідну і достатню систему рівнянь для розв’язку задач механіки суцільних середовищ.

Ці рівняння для довільного об’єму V суцільного середовища, обмеженого замкнутою поверхнею S (рис. 5.5), базуються на використанні принципу д’Аламбера.

У загальному випадку на даний об’єм діють:

об’ємні сили 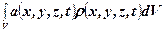з вектором прискорень а,

поверхневі сили 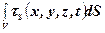з вектором напружень t_S,

сили інерції з вектором прискорень ,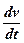

де 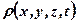– густина середовища.

Вектор напружень визначається через компоненти тензора напружень (5.1)

,

де i, j, k – орти декартової системи координат.

Рівняння руху суцільного середовища визначаються з умов рівності нулю головного вектора та головного моменту всіх сил і в інтегральній формі мають вигляд

; (5.14)

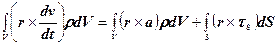, (5.15)

де 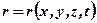–радіус-вектор точки у вибраній системі координат (рис. 5.5)

Рівняння (5.15) вказує на симетрію тензора напружень (5.1), і апріорі приймаючи симетрію Т_s, можна його не використовувати.

Рівняння (5.14) у векторній диференціальній формі матиме вигляд

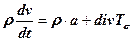. (5.16)

Похідна характеризує зміну швидкості матеріальної точки суцільного середовища, що переміщується у просторі і називається субстанційною похідною.

Вона визначається як

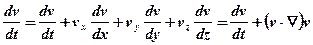, (5.17)

де – операція Гамільтона.

Перший доданок 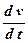називається локальною похідною і характеризує зміну швидкості у фіксованій точці простору з часом, а другий доданок – конвективною похідною і характеризує зміну швидкості при переміщенні з однієї точки в іншу.

Дата добавления: 2014-11-29