Многоалфавитные подстановки

Пропорциональные шифры

К одноалфавитным методам подстановки относятся пропорциональные или монофонические шифры, в которых уравнивается частота появления зашифрованных знаков для защиты от раскрытия с помощью частотного анализа. Для знаков, встречающихся часто, используется относительно большое число возможных эквивалентов. Для менее используемых исходных знаков может оказаться достаточным одного или двух эквивалентов. При шифровании замена для символа открытого текста выбирается либо случайным, либо определенным образом (например, по порядку).

При использовании пропорционального шифра в качестве замены символам обычно выбираются числа.

Интересно, что шифры, в которых производится замена букв несколькими символами, пропорционально встречаемости в открытом тексте, описывали итальянские ученые еще в XIV-XV веках.

Пропорциональные шифры более сложны для вскрытия, чем шифры простой одноалфавитной замены. Однако, если имеется хотя бы одна пара "открытый текст – шифротекст", вскрытие производится тривиально. Если же в наличии имеются только шифротексты, то вскрытие ключа, то есть нахождение таблицы замен, становится более трудоемким, но тоже вполне осуществимым.

В целях маскирования естественной частотной статистики исходного языка применяется многоалфавитная подстановка, которая также бывает нескольких видов. В многоалфавитных подстановках для замены символов исходного текста используется не один, а несколько алфавитов. Обычно алфавиты для замены образованы из символов исходного алфавита, записанных в другом порядке.

Примером многоалфавитной подстановки может служить схема, основанная на использовании таблицы Вижинера. Этот метод, известный уже в XVI веке, был описан французом Блезом Вижинером в "Трактате о шифрах", вышедшем в 1585 году.

В этом методе для шифрования используется таблица, представляющая собой квадратную матрицу с числом элементов NxN, где N — количество символов в алфавите (таблица 2.6). В первой строке матрицы записывают буквы в порядке очередности их в исходном алфавите, во второй — ту же последовательность букв, но с циклическим сдвигом влево на одну позицию, в третьей — со сдвигом на две позиции и т. д.

Таблица 2.6. Подготовка таблицы шифрования

АБВГДЕ..................ЭЮЯ

БВГДЕЖ..................ЮЯА

ВГДЕЖЗ..................ЯАБ

ГДЕЖЗИ...................АБВ

ДЕЖЭИК...................БВГ

ЕЖЗИКЛ...................ВГД

...........

..........

ЯАБВГД...................ЬЭЮ

Для шифрования текста выбирают ключ, представляющий собой некоторое слово или набор символов исходного алфавита. Далее из полной матрицы выписывают подматрицу шифрования, включающую первую строку и строки матрицы, начальными буквами которых являются последовательно буквы ключа (например, если выбрать ключ "весна", то таблица шифрования будет такой, как на таблица 2.7).

Таблица 2.7. Первый этап шифрования – составление подматрицы шифрования

АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

ВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБ

ЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГД

НОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМ

СТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМНОПР

В процессе шифрования (рис. 3.5.5) под каждой буквой шифруемого текста записывают буквы ключа, повторяющие ключ требуемое число раз, затем шифруемый текст по таблице шифрования (таблица 2.7) заменяют буквами, расположенными на пересечениях линий, соединяющих буквы текста первой строки таблицы и буквы ключа, находящейся под ней.

Например, под первой буквой исходного текста "М" записана буква "В" ключа. В таблице кодирования находим столбец, начинающийся с "М" и строку, начинающуюся с "В". На их пересечении располагается буква "О". Она и будет первым символом зашифрованного сообщения (на рис. 2.5 эта буква выделена прямоугольной рамочкой). Следующая буква исходного сообщения – "Е", символ ключа – тоже "Е". Находим пересечение строки, начинающейся с "Е", и столбца, начинающегося с "Е". Это будет буква "Л" – второй символ зашифрованного сообщения.

Рис. 3.5.5. Механизм шифрования многоалфавитной заменой

Рассмотрим на примере процесс расшифрования сообщения по методу Вижинера. Пусть имеется зашифрованное с помощью ключа ВЕСНА сообщение КЕКХТВОЭЦОТССВИЛ (пробелы при шифровании пропущены). Расшифровка текста выполняется в следующей последовательности (таблица 2.8):

над буквами шифрованного текста сверху последовательно записывают буквы ключа, повторяя ключ требуемое число раз;

в строке подматрицы таблицы Вижинера для каждой буквы ключа отыскивается буква, соответствующая знаку шифрованного текста. Находящаяся над ней буква первой строки и будет знаком расшифрованного текста;

полученный текст группируется в слова по смыслу.

КЛЮЧ

ВЕСНАВЕСНАВЕСНАВ

ЗАШИФРОВАННЫЙ ТЕКСТ

КЕКХТВОЭЦОТССВИЛ

РАСШИФРОВАННЫЙ ТЕКСТ

ЗАЩИТАИНФОРМАЦИИ

ИСХОДНЫЙ ТЕКСТ

ЗАЩИТА ИНФОРМАЦИИ

Раскрыть шифр Вижинера, тем же способом, что и шифр одноалфавитной замены, невозможно, так как одни и те же символы открытого текста могут быть заменены различными символами зашифрованного текста. С другой стороны, различные буквы открытого текста могут быть заменены одинаковыми знаками зашифрованного текста.

Особенность данного метода многоалфавитной подстановки заключается в том, что каждый из символов ключа используется для шифрования одного символа исходного сообщения. После использования всех символов ключа, они повторяются в том же порядке. Если используется ключ из десяти букв, то каждая десятая буква сообщения шифруется одним и тем же символом ключа. Этот параметр называется периодом шифра. Если ключ шифрования состоит из одного символа, то при шифровании будет использоваться одна строка таблицы Вижинера, следовательно, в этом случае мы получим моноалфавитную подстановку, а именно шифр Цезаря.

С целью повышения надежности шифрования текста можно использовать подряд два или более зашифрования по методу Вижинера с разными ключами (составной шифр Вижинера).

На практике кроме метода Вижинера использовались также различные модификации этого метода. Например, шифр Вижинера с перемешанным один раз алфавитом. В этом случае для расшифрования сообщения получателю необходимо кроме ключа знать порядок следования символов в таблице шифрования.

Еще одним примером метода многоалфавитной подстановки является шифр с бегущим ключом или книжный шифр. В этом методе один текст используется в качестве ключа для шифрования другого текста. В эпоху "докомпьютерной" криптографии в качестве ключа для шифра с бегущим ключом выбирали какую-нибудь достаточно толстую книгу; от этого и произошло второе название этого шифра. Периодом в таком методе шифрования будет длина выбранного в качестве ключа произведения.

Методы многоалфавитной подстановки, в том числе и метод Вижинера, значительно труднее поддаются "ручному" криптоанализу. Для вскрытия методов многоалфавитной замены разработаны специальные, достаточно сложные алгоритмы. С использованием компьютера вскрытие метода многоалфавитной подстановки возможно достаточно быстро благодаря высокой скорости проводимых операций и расчетов.

В первой половине ХХ века для автоматизации процесса выполнения многоалфавитных подстановок стали широко применять роторные шифровальные машины. Главными элементами в таких устройствах являлись роторы – механические колеса, используемые для выполнения подстановки. Роторная шифровальная машина содержала обычно клавиатуру и набор роторов. Каждый ротор содержал набор символов (по количеству в алфавите), размещенных в произвольном порядке, и выполнял простую одноалфавитную подстановку. После выполнения первой замены символы сообщения обрабатывались вторым ротором и так далее. Роторы могли смещаться, что и задавало ключ шифрования. Некоторые роторные машины выполняли также и перестановку символов в процессе шифрования. Самым известным устройством подобного класса являлась немецкая шифровальная роторная машина Энигма (лат. Enigma — загадка), использовавшаяся во время второй мировой войны. Выпускалось несколько моделей Энигмы с разным числом роторов. В шифрмашине Энигма с тремя роторами можно было использовать 16900 разных алфавитов, и все они представляли собой различные перестановки символов.

on_load_lecture(); Методы гаммирования

Еще одним частным случаем многоалфавитной подстановки является гаммирование. В этом способе шифрование выполняется путем сложения символов исходного текста и ключа по модулю, равному числу букв в алфавите. Если в исходном алфавите, например, 33 символа, то сложение производится по модулю 33. Такой процесс сложения исходного текста и ключа называется в криптографии наложением гаммы.

Пусть символам исходного алфавита соответствуют числа от 0 (А) до 32 (Я). Если обозначить число, соответствующее исходному символу, x, а символу ключа – k, то можно записать правило гаммирования следующим образом:

z = x + k (mod N),

где z – закодированный символ, N - количество символов в алфавите, а сложение по модулю N - операция, аналогичная обычному сложению, с тем отличием, что если обычное суммирование дает результат, больший или равный N, то значением суммы считается остаток от деления его на N. Например, пусть сложим по модулю 33 символы Г (3) и Ю (31):

3 + 31 (mod 33) = 1,

то есть в результате получаем символ Б, соответствующий числу 1.

Наиболее часто на практике встречается двоичное гаммирование. При этом используется двоичный алфавит, а сложение производится по модулю два. Операция сложения по модулю 2 часто обозначается , то есть можно записать:

Операция сложения по модулю два в алгебре логики называется также "исключающее ИЛИ" или по-английски XOR.

Рассмотрим пример. Предположим, нам необходимо зашифровать десятичное число 14 методом гаммирования с использованием ключа 12. Для этого вначале необходимо преобразовать исходное число и ключ (гамму) в двоичную форму: 14₍₁₀₎=1110₍₂₎, 12₍₁₀₎=1100₍₂₎. Затем надо записать полученные двоичные числа друг под другом и каждую пару символов сложить по модулю два. При сложении двух двоичных знаков получается 0, если исходные двоичные цифры одинаковы, и 1, если цифры разные:

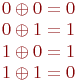
Сложим по модулю два двоичные числа 1110 и 1100:

Исходное число 1 1 1 0

Гамма 1 1 0 0

Результат 0 0 1 0

В результате сложения получили двоичное число 0010. Если перевести его в десятичную форму, получим 2. Таким образом, в результате применения к числу 14 операции гаммирования с ключом 12 получаем в результате число 2.

Каким же образом выполняется расшифрование? Зашифрованное число 2 представляется в двоичном виде и снова производится сложение по модулю 2 с ключом:

Зашифрованное число 0 0 1 0

Гамма 1 1 0 0

Результат 1 1 1 0

Переведем полученное двоичное значение 1110 в десятичный вид и получим 14, то есть исходное число.

Таким образом, при гаммировании по модулю 2 нужно использовать одну и ту же операцию как для зашифрования, так и для расшифрования. Это позволяет использовать один и тот же алгоритм, а соответственно и одну и ту же программу при программной реализации, как для шифрования, так и для расшифрования.

Операция сложения по модулю два очень быстро выполняется на компьютере (в отличие от многих других арифметических операций), поэтому наложение гаммы даже на очень большой открытый текст выполняется практически мгновенно. Благодаря указанным достоинствам метод гаммирования широко применяется в современных технических системах сам по себе, а также как элемент комбинированных алгоритмов шифрования.

Сформулируем, как производится гаммирование по модулю 2 в общем случае:

- символы исходного текста и гамма представляются в двоичном коде и располагаются один под другим, при этом ключ (гамма) записывается столько раз, сколько потребуется;

- каждая пара двоичных знаков складывается по модулю два;

- полученная последовательность двоичных знаков кодируется символами алфавита в соответствии с выбранным кодом.

При использовании метода гаммирования ключом является последовательность, с которой производится сложение – гамма. Если гамма короче, чем сообщение, предназначенное для зашифрования, гамма повторяется требуемое число раз.

Чем длиннее ключ, тем надежнее шифрование методом гаммирования. На практике длина ключа ограничена возможностями аппаратуры обмена данными и вычислительной техники, а именно выделяемыми объемами памяти под ключ, временем обработки сообщения, а также возможностями аппаратуры подготовки и записи последовательностей ключей. Кроме того, для использования ключа вначале необходимо каким-либо надежным способом доставить его обеим сторонам, обменивающимся сообщениями. Это приводит к возникновению проблемы распределения ключей, сложность решения которой возрастает с увеличением длины ключа и количества абонентов в сети передачи сообщений.

Дата добавления: 2014-11-29