Методы перестановки

При использовании шифров перестановки входной поток исходного текста делится на блоки, в каждом из которых выполняется перестановка символов. Перестановки в классической "докомпьютерной" криптографии получались в результате записи исходного текста и чтения шифрованного текста по разным путям геометрической фигуры.

Простейшим примером перестановки является перестановка с фиксированным периодом d. В этом методе сообщение делится на блоки по d символов и в каждом блоке производится одна и та же перестановка. Правило, по которому производится перестановка, является ключом и может быть задано некоторой перестановкой первых d натуральных чисел. В результате сами буквы сообщения не изменяются, но передаются в другом порядке.

Например, для d=6 в качестве ключа перестановки можно взять 436215. Это означает, что в каждом блоке из 6 символов четвертый символ становится на первое место, третий – на второе, шестой – на третье и т.д.

Для повышения криптостойкости можно последовательно применить к шифруемому сообщению две или более перестановки с разными периодами.

Другим примером методов перестановки является перестановка по таблице. В этом методе производится запись исходного текста по строкам некоторой таблицы и чтение его по столбцам этой же таблицы. Последовательность заполнения строк и чтения столбцов может быть любой и задается ключом.

В случае, если размер сообщения не кратен размеру блока, можно дополнить сообщение какими-либо символами, не влияющими на смысл, например, пробелами. Однако это делать не рекомендуется, так как это дает противнику в случае перехвата криптограммы информацию о размере используемой таблицы перестановок (длине блока). После определения длины блока противник может найти длину ключа (количество столбцов таблицы) среди делителей длины блока.

Посмотрим, как зашифровать и расшифровать сообщение, имеющее длину, не кратной размеру таблицы перестановки. Зашифруем слово

ПЕРЕМЕНКА

Количество символов в исходном сообщении равно 9. Запишем сообщение в таблицу по строкам (таблица 2.9), а последние три ячейки оставим пустыми

.

Таблица 2.10. Шифрование неполного блока методом перестановки по таблице

П Е Р Е М Е Н К А

Затем будем считывать из таблицы последовательно по столбцам:

ПМАЕЕРНЕК

Для расшифрования вначале определяют число полных столбцов, то есть количество символов в последней строке. Для этого делят размер сообщения (в нашем примере – 9) на количество столбцов или размер ключа (в примере – 4). Остаток от деления будет числом полных столбцов: 9 mod 4 = 1. Следовательно, в нашем примере был 1 полный столбец и три коротких. Теперь можно поставить буквы сообщения на свои места и расшифровать сообщение. Так как ключом при шифровании было число 1234 (столбцы считывались последовательно), то при расшифровании первые три символа (ПМА) записываются в первый столбец таблицы перестановки, следующие два (ЕЕ) – во второй столбец, следующие два (РН) – в третий, и последние два (ЕК) – в четвертый. После заполнения таблицы считываем строки и получаем исходное сообщение ПЕРЕМЕНКА.

Существуют и другие способы перестановки, которые можно реализовать программным и аппаратным путем. Например, при передаче данных, записанных в двоичном виде, удобно использовать аппаратный блок, который перемешивает определенным образом с помощью соответствующего электрического монтажа биты исходного n-разрядного сообщения. Так, если принять размер блока равным восьми битам, можно, к примеру, использовать такой блок перестановки, как на рис. 2.7.

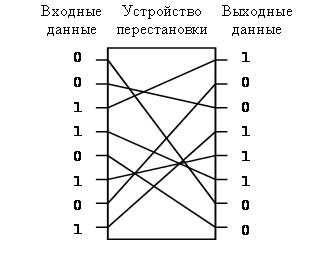
Рис. 2.7. Аппаратный блок перестановки

Для расшифрования на приемной стороне устанавливается другой блок, восстанавливающий порядок цепей.

Аппаратно реализуемая перестановка широко используется на практике как составная часть некоторых современных шифров.

При перестановке любого вида в зашифрованное сообщение будут входить те же символы, что и в открытый текст, но в другом порядке. Следовательно, статистические закономерности языка останутся без изменения. Это дает криптоаналитику возможность использовать различные методы для восстановления правильного порядка символов.

Если у противника есть возможность пропускать через систему шифрования методом перестановки специально подобранные сообщения, то он сможет организовать атаку по выбранному тексту. Так, если длина блока в исходном тексте равна N символам, то для раскрытия ключа достаточно пропустить через шифровальную систему N-1 блоков исходного текста, в которых все символы, кроме одного, одинаковы. Другой вариант атаки по выбранному тексту возможен в случае, если длина блока N меньше количества символов в алфавите. В этом случае можно сформировать одно специальное сообщение из разных букв алфавита, расположив их, например, по порядку следования в алфавите. Пропустив подготовленное таким образом сообщение через шифровальную систему, специалисту по криптоанализу останется только посмотреть, на каких позициях очутились символы алфавита после шифрования, и составить схему перестановки.

on_load_lecture(); Ключевые термины

Гаммирование – метод шифрования, основанный на "наложении" гамма-последовательности на открытый текст. Обычно это суммирование в каком-либо конечном поле (суммирование по модулю). Например, в поле GF(2) такое суммирование принимает вид обычного "исключающего ИЛИ". При расшифровке операция проводится повторно, в результате получается открытый текст.

Пропорциональные или монофонические шифры – методы замены, в которых уравнивается частота появления зашифрованных знаков.

Шифры замены (подстановки) основаны на том, что символы исходного текста, обычно разделенные на блоки и записанные в одном алфавите, заменяются одним или несколькими символами другого алфавита в соответствии с принятым правилом преобразования.

Шифр многоалфавитной замены (или подстановки) – группа методов шифрования подстановкой, в которых для замены символов исходного текста используется не один, а несколько алфавитов по определенному правилу.

Шифры перестановки основаны на том, что входной поток исходного текста делится на блоки, в каждом из которых выполняется перестановка символов. Ключом такого шифра является используемая при шифровании перестановочная матрица или вектор, указывающий правило перестановки.

Шифр простой (или одноалфавитной) замены, простой подстановочный шифр, моноалфавитный шифр — группа методов шифрования, которые сводятся к созданию по определённому алгоритму таблицы шифрования, в которой для каждой буквы открытого текста существует единственная сопоставленная ей буква шифртекста. Само шифрование заключается в замене букв согласно таблице. Для расшифровки достаточно иметь ту же таблицу, либо знать алгоритм, по которой она генерируется.

Симметричное шифрование (шифрование с закрытым ключом) – методы обратимого преобразования данных, в которых используется один и тот же ключ, который обе стороны информационного обмена должны хранить в секрете от противника. Все известные из истории шифры, например, шифр Цезаря – это шифры с закрытым ключом.

Дата добавления: 2014-11-29