Основные уравнения электромагнитного поля

См. Maxwell. Treatise on Electricity and Magnetism, Vol. II §§ 822 и 831 (в отделе — On the hypothesis of Molecular Vortices).

Обратимся к выводу основных соотношений, характеризующих явления электромагнитного поля. Исходным пунктом этого вывода служат два соотношения, уже известные из предыдущих глав, именно? закон магнитодвижущей силы (10):

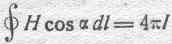
и закон электродвижущей силы (45):

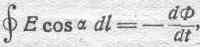
где оба интеграла взяты по замкнутым контурам. Отметим, кстати, что написанные соотношения по существу именно и выражают собою взаимную зависимость величин Е и Н, о которой мы гово­рили в предыдущем параграфе. Дальнейшие математические опе­рации имеют целью более отчетливое выявление этой зависимости, а также изучение главнейших результатов, из нее вытекающих.

При обследовании явлений электромагнитного поля будем поль­зоваться декартовыми координатами. Векторы Е и Н будем для каждой точки пространства определять их проекциями на оси координат.

Расположение координатных осей примем, по Максвеллу, соответствующее системе правого винта (штопора). При этом будет соблюдаться основное геометрическое соотношение между напра­влениями тока и магнитного поля (правило штопора). Для переме­щения винта штопора вдоль одной из координатных осей нужно будет вращать его рукоятку в плоскости двух других осей в на­правлении циклической перестановки букв х, у, z, т. е. от преды­дущей буквы алфавита к последующей (так как осей три: OX, OY, OZ, то буквой, следующей за z, следует считать х). Таким образом,

для движения винта штопора вдоль оси OZ необходимо рукоятке его сообщить вращение от оси ОХ к оси OY; для движения вдоль оси ОХ— вращение От OY к OZ; для движения вдоль оси OY — вращение от OZ к ОХ. Если, следовательно, ось ОХ направлена к востоку и ось OY —к северу, то ось OZ должна быть направлена вверх. Такому условию удовлетворяет расположение осей, предста­вленное на рисунке 177.

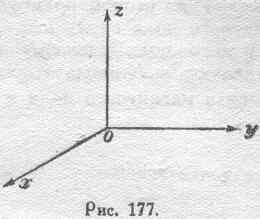
Обозначим составляющие векторов: силы электрического поля Е, силы магнитного поля Н, магнитной ин­дукции В и плотности тока J, па­раллельные трем координатным осям, соответственно через:

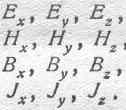
Векторы Е, Н, В и J в каждой данной точке являются, вообще говоря, функциями координат этой точки и времени, т. е.:

Очевидно, что и составляющие Е, Н, В и J по координатным осям являются также функциями х, у,,z, t.

Для получения дифференциальных урав­нений, выражающих теорию Максвелла и характеризующих процессы, происхо­дящие в электромагнитом поле, обратимся к упомянутым законам: закону магнито­движущей силы и закону электродвижущей силы. Рассмотрим в электромагнитном поле какую-нибудь элементарную площадку прямоугольной формы со сторонами dy и dz (рис. 178).

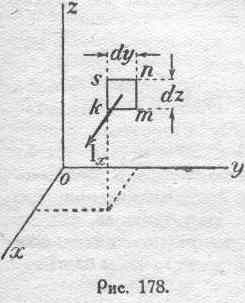
Применим к контуру kmns, охватывающему ату площадку, закон магнитодвижущей силы (10):

Обратимся сначала к правой части этого равенства. Составляю­щую, параллельную оси ОХ, плотности тока (J), проходящего через данную площадку, мы обозначили через J_х. Стало быть, полный ток через площадку dydz будет равен

J_xdydz.

Далее остановимся на левой части исходного равенства (10). Найдем сумму произведений:

Hcosadl

по сторонам взятого прямоугольника. Так как стороны прямоуголь­ника kmns параллельны осям OY и OZ, то величина Нcosa Для каждой из сторон прямоугольника равна составляющей силы ма­гнитного поля вдоль оси OY или OZ. Пусть в точке k сила ма­гнитного поля равна Н и, следовательно, соответствующие со­ставляющие Н вдоль сторон km и ks равны Н и Н_z. Далее, в точке т сила магнитного поля и ее составляющие выразятся по схеме:

а в точке s:

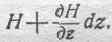
Тогда произведение Нcosadl для стороны прямоугольника km можно выразить (отбрасывая бесконечно-малые, исключающиеся при обходе контура kmns, и пренебрегая бесконечно малыми высших порядков) через составляющую силы магнитного поля вдоль оси О Y таким образом:

H_ydy.

Для стороны mn это произведение окажется равным

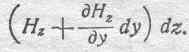
При дальнейшем обходе прямоугольника kmns знаки при про­изведениях Нcosadl необходимо переменить на обратные, так как приходится итти в направлении, противоположном положительному направлению осей OY и OZ. Таким образом, для стороны ns имеем:

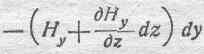
и, наконец, для стороны sk:

-H_zdz.

Суммируя эти слагаемые, получим:

Раскроем скобки:

По сокращении в левой части имеем:

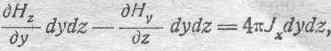
откуда получаем окончательно:

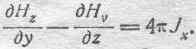
Совершенно аналогичными рассуждениями получим для некото­рой площадки, параллельной плоскости XOZ, уравнение:

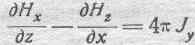
и для площадки, параллельной плоскости XOY, уравнение:

Полученные уравнения не выражают еще ничего принципиально нового. Они представляют собою лишь одну из возможных форм (в данном случае дифференциальную) общеизвестного закона, что нет элек­трического тока без магнитного поля. Представляет интерес такое пре­образование полученных уравнений, в результате которого в правой части вместо плотности тока J входит сила электрического поля Е. Для выполне­ния этого преобразования выразим плот­ность тока J через величину Е. Так как мы не делали при выводе уравне­ний никаких оговорок относительно свойств среды, в которой происходит электромагнитный процесс, то можем себе представить, что протекающий по этой среде электрический ток состоит из двух слагаемых: проводникового тока и тока смещения.

Сила проводникового тока равна, согласно закону Ома, электродвижущей силе, деленной на сопротивление. Чтобы определить ЭДС в данном случае, построим на нашей площадке рисунка 178 параллелепипед dxdydz (рис. 179).

Тогда, если составляющая силы электрического поля в направлении оси ОХ равна E_х, то ЭДС, действующая вдоль ребра dx рассматриваемого параллелепипеда, равна E_xdx.

Сопротивление параллепипеда dxdydz будет

где r— удельное сопротивление среды. Следовательно, проводни­ковый ток сквозь площадку dydz выразится так:

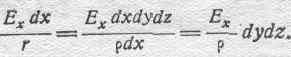
Плотность тока смещения равна, как известно, производной от электрического смещения по времени, т. е. в данном случае, по­лагая e=const, получим:

Следовательно, ток смещения сквозь площадку dydz равен

Полный ток сквозь площадку dydz выразится суммою токов проводникового и тока смещения; т. е.

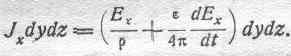
Следовательно,

Аналогично получим:

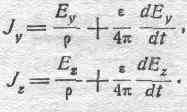
Подставляя полученные значения в выведенные выше уравнения, получаем:

Такова окончательная форма первой группы уравнений электро­магнитного поля. Именно в такой форме эти уравнения были даны Максвеллом.

Аналогичную систему уравнений дает закон электродвижущей силы (45):

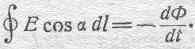
Взяв в электромагнитном поле элементарную площадку со сторонами dy и dz, пронизываемую некоторым магнитным потоком Ф,

и составляя для ее сторон сумму выражений Ecosadl, получим, совершенно аналогично предыдущему, для левой части уравнения электродвижущей силы выражение:

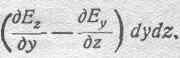
Что касается правой части уравнения, то поток Ф, пронизы­вающий площадку dydz, мы можем определить, умножая нормальную составляющую магнитной индукции В_х (для площадки, параллель­ной плоскости YOZ) на площадь dydz, т. е.

Ф_x=B_xdydz.

Таким образом, получаем уравнение:

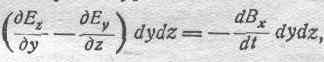
которое по сокращении на dydz принимает вид:

Взяв площадки, параллельные координатным плоскостям ZOX и XOY, получим два другие уравнения, выражающие зависимость между составляющими силы электрического поля и составляющими магнитной индукции. Для плоскости XOZ получаем:

и для плоскости XOY:

Наконец, для случая m=const, вторая группа интересующих нас уравнений принимает вид:

Таким образом, мы получили систему из шести дифференциаль­ных уравнений электромагнитного поля, или так называемых уравнений Максвелла, для случая e=const и m=const. Собственно говоря, вторая группа этих уравнений, т. е. уравнения (134), не была дана Максвеллом именно в той форме, как мы их напи­сали. Но так как содержание этих уравнений по существу входит в общие дифференциальные уравнения электромагнитного поля, данные Максвеллом, то мы и будем называть максвелловыми уравнениями всю совокупность уравнений (133) и (134).

§ 120. Общий характер дифференциальных уравнений электро­магнитного поля,

Остановимся вкратце на некоторых сторонах физического со­держания уравнений (133) и (134). Основное, что выражают собой эти уравнения электромагнитного поля, — это взаимная связанность векторов, характеризующих электрическое и магнитное поля.

Всякое изменение силы магнитного поля Н во времени влечет за собою изменения в пространственном распределении вектора электрической силы Е и, обратно, всякое изменение Е во времени обусловливает, вообще говоря, изменения в пространственном распределении вектора Н,

Кроме того, так как в уравнения (133) и (134) входят соста­вляющие Е и Н по координатным осям, то эти уравнения дают возможность судить не только о количественных соотношениях между Е и H, но и о взаимной ориентировке их взаимно связанных изменений. Например, изменение во времени составляющей силы магнитного поля вдоль оси ОХ вызывает изменения в распреде­лении составляющих силы электрического поля в плоскости, па­раллельной YOZ, т. е. в плоскости, перпендикулярной оси ОХ, и т. д.

Мы сказали, что всякое изменение вектора Н (или Е) во вре­мени связано с изменением распределения вектора Е (или H) в пространстве. В связи с этим, вообще говоря, изменение одного влечет за собой появление другого или, следовательно, появление одного связано с появлением другого.

Остановимся еще на том, как в написанных уравнениях отра­жается разница между характером электромагнитного процесса в случае диэлектрика и в случае проводника.

Если мы имеем абсолютный диэлектрик, то r=¥ и, следо­вательно, проводникового тока не существует. Уравнения (133) принимают вид (для простоты выпишем только одно из них):

Следовательно, в случае абсолютного диэлектрика, для появле­ния такого магнитного поля, в котором могут иметь место замкну­тые контуры с магнитодвижущей силой, не равной нулю, иными словами, для возникновения электрического тока, необходимо изме­нение В во времени. Указанное обстоятельство, между прочим, является математическим выражением того, что передача энергии постоянным током, т. е. при постоянной электродвижущей силе, невозможна в случае отсутствия проводника, так как при этом в системе не может возникнуть постоянный электрический ток.

Рассмотрим другой предельный случай, когда r, конечно и про­водниковый ток существует. Допустим еще, что

Е =const.

То же самое уравнение принимает тогда вид:

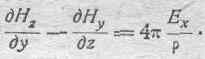
Иными словами, в этом случае для появления Н, т. е. для воз­никновения электрического тока, достаточно самого факта сущест­вования Е, хотя бы и неизменного во времени. Таким образом, вводя в систему проводник, мы создаем такие условия, при которых в ней может возникнуть электрический ток и при постоянном зна­чении электродвижущей силы.

Дата добавления: 2014-11-29