Распространение тока в металлических массах. Поверхностный аффект

J. Pointing. Le mode de propagation de l'energie et de la tension electrique dans le champ electromagnetique. Rapports presentes au Congres International de Physique reuni a Paris en 1900, vol. II, p. 284.

В предыдущих параграфах настоящей главы были обследованы общие законы распространения электромагнитной энергии. Остано­вимся теперь на более детальном рассмотрении процесса движения энергии в проводящей среде после того, как энергия вошла в эту среду из диэлектрика.

Изучение происходящих при этом явлений особо интересно потому, что, как опыт показывает, при распространении перемен­ного тока в металлических массах наблюдаются уклонения от обыч­ных законов распределения тока по сечению проводника: именно, в то время как при постоянном токе плотность его по всему сече­нию проводника равномерна, при переменном токе, особенно при высоких частотах, замечаются значительные отступления от этой

равномерности, причем, чем дальше от поверхности проводника, тем меньшей оказывается плотность тока, и тем больше ток отстает по фазе от напряжения. Это явление — неравномерное распределе­ние тока по сечению проводника—получило название поверхно­стного эффекта.

В силу поверхностного распределения тока, активной частью проводника, „несущей" ток при высоких частотах, является только более или менее незначительная его доля, прилегающая к наружной поверхности. Части проводника, более близкие к его оси, оказы­ваются при этих частотах почти лишенными тока и не принимаю­щими, практически, участия в электрокинетическом процессе. Все происходит так, как будто проводник не представляет собою сплош­ной массы, а является полым внутри. Если вспомнить, что сопро­тивление проводника находится в обратно-пропорциональной зависи­мости от площади его поперечного сечения, при чем предполагается, что все это сечение пронизывается электрическим током, то станет ясно, что уменьшение активной части сечения проводника эквива­лентно увеличению его омического сопротивления. Чем выше частота, тем меньшая часть поперечного сечения проводника оказывается нагруженной током, тем больше, стало быть, действую­щее омическое сопротивление этого проводника.

Необходимо здесь отметить, что при таких условиях, т. е. при явлении поверхностного распределения тока, внутренняя, т. е. при­легающая к оси часть проводника оказывается совершенно беспо­лезной и лишь удорожает стоимость проводки, так как увеличивает количество затраченного металла. Поэтому в установках, работаю­щих при таких высоких частотах, при которых явление поверхно­стного эффекта уже резко выражено, часто употребляют или полые проводники, или же проводники, составленные из очень большого числа тонких изолированных проволочек, благодаря чему достигается значительное увеличение полезной поверхности проводника при данном его сечении.

При изучении всякого явления бывает полезно составить себе, для уяснения механизма явления, более или менее простую рабо­чую схему, помогающую связать происходящее явление с какими-либо конкретными и знакомыми представлениями. В качестве такой схемы для данного случая можно предложить следующее. Мы можем представить себе всякий проводник состоящим из ряда цилиндрических коаксиальных элементов малого сечения, располо­женных вокруг его оси. Не трудно убедиться, что элементы, распо­ложенные у периферии проводника, связаны с меньшим магнитным потоком, чем элементы, лежащие внутри проводника. В самом деле, в то время как с первыми связан лишь магнитный поток, наводящийся вне проводника, магнитный поток, связанный с вну­тренними элементами, больше на величину потока, распределенного внутри металла. При переменном токе, связанный с током магнит­ный поток является также переменным. Всякое же изменение маг­нитного потока связано с возникновением в проводнике обратной ЭДС. На основании только что сказанного, мы должны притти

к заключению, что во внутренних элементах провода будет индук­тироваться большая обратная ЭДС, чем во внешних. Влияние этой обратной ЭДС сказывается, во первых, в ослаблении силы тока и, во-вторых, в появлении разности фаз между током и напряжением. По приведенной схеме оказывается совершенно ясным, что внутренние элементы проводника, как связанные с большим магнитным потоком, представят большее полное сопротивление (z) и обусловят больший сдвиг тока по фазе.

Перейдем теперь к математическому обследованию вопроса. Обратимся к уже известный нам уравнениям Максвелла в той их форме, которую можно применить к случаю проводникового тока, именно, возьмем уравнения, связывающие силу тока с силою магнитного поля (см. § 119):

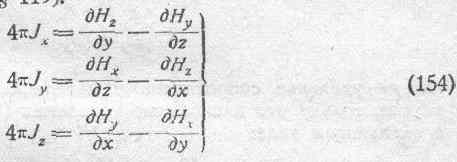
Будем здесь рассматривать J_x, J_y и J_z как составляющие плот­ности чисто проводникового тока. При этом, вообще говоря, плот­ность тока J является функцией геометрических, координат и вре­мени, т. е:

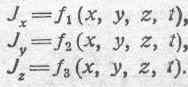
Возьмем первое из уравнений (154) и умножим обе его части на величину магнитной проницаемости m. Так как мы предположим, что имеем дело со средой, для которой m=const, и так как В=mН, т. е.:

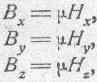
то, вводя в правой части уравнения m под. знак производной, получим:

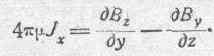
Возьмем производную от полученного уравнения по времени:

*

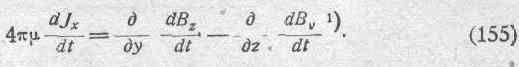Но на основании второй группы уравнений Максвелла (136)

имеем:

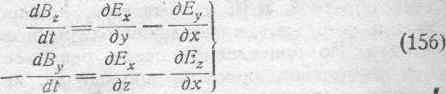
Составляющие же электрического поля Е_х, Е_у и E_z, в случае проводникового тока, представляют собою падение напряжения на длине в 1 см по направлению соответственной оси, т. е. мы имеем право написать:

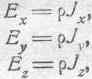
где r — удельное сопротивление материала проводника. Следова­тельно, только что написанные уравнения (156) можно представить в следующем виде:

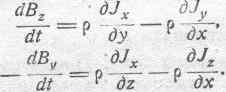
Подставляя эти выражения в уравнения (155), получим:

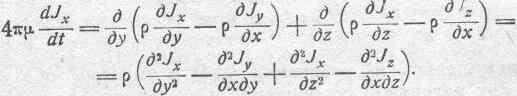
Прибавив и отняв от правой части равенства величину:

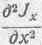
получим следующее уравнение: (157)

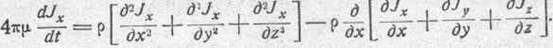
Выражение:

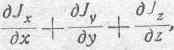
представляющее собою сумму частных производных по трем гео­метрическим координатам от составляющих плотности тока, равно нулю, что легко показать. Именно, возьмем группу уравнений

Максвелла (154) и, продифференцировав эти три уравнения со­ответственно по х, по у и по z, получим:

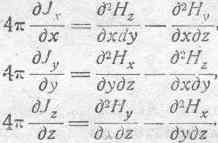
Сложим эти уравнения почленно. При этом правая часть урав­нения даст нуль. Таким образом, получаем:

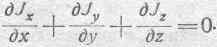
Итак, уравнение (157) принимает вид:

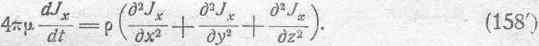
Совершенно аналогичными рассуждениями можно получить два других уравнения:

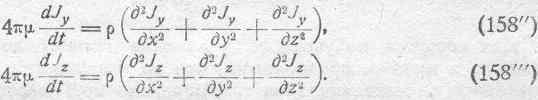
Эти уравнения вполне определяют характер распределения тока в металлических массах, так как они связывают математически изменение тока во времени с из­менением его по всем геометри­ческим координатам. По форме эти уравнения вполне тождественны уравнениям, определяющим те­чение теплоты вследствие тепло­проводности. Отсюда непосред­ственно следует, что со стороны формальной проникновение токов внутрь массы металла совершается по тем же законам, что и про­никновение тепла от нагретой по­верхности внутрь тела. С целью общего исследования закона распределения электрического тока в массе проводника решим по­лученные уравнения (158) для простейшего частного случая. Пусть (рис. 191) по поверхности раздела ABCD, являющейся одновременно координатной плоскостью YOZ, существует равномерное распре­деление переменного тока.

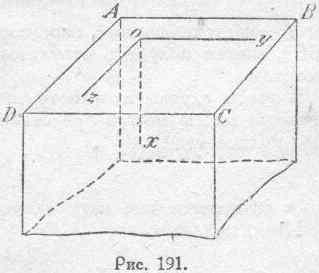
Ось ОХ направим вниз, т, е. в тело

проводника. Допустим далее, что этот переменный ток ориентиро­ван в направлении параллельном оси OZ, Тогда будем иметь:

J_x =0

и

J_y =0.

Если поверхность раздела ABCD, а также и масса проводника, безгранично велики и, следовательно, нет причин для изменения ориентировки тока, то эта последняя на любой глубине будет одна и та же. На поверхности раздела плотность тока имеет вследствие равномерности распределения одно и то же значение для всех точек. Плотность тока J _г на любой глубине будет зависеть только от времени t и геометрической координаты х:

J_z=f(t,x).

При наличии же данного условия уравнение (158'") примет

вид:

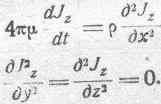
Для решения полученного уравнения примем дополнительное условие, а именно, предположим, что по поверхности раздела течет гармонически изменяющийся ток, определяемый некоторым выраже­нием вида:

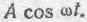
Здесь:

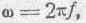
где f — частота данного переменного тока. Придавая f любое зна­чение, можем получить результат, соответствующий каким угодно

частотам.

В таком случае плотность тока в любой точке внутри метал­лической массы можно представить вещественной частью комплекс­ного количества:

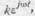
где e, есть основание натуральных логарифмов, a j=Ö-1. Итак, полагаем:

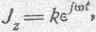(159)

и подставляем эго значение для J_z в уравнение:

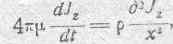
не забывая только, что реальное значение плотности силы тока равно вещественной части данного комплекса. Произведя указанную подстановку, получим:

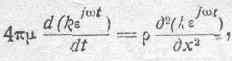
что дает по дифференцировании (если принять во внимание, что k зависит от x: и не зависит от t):

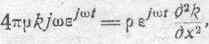
или по сокращении на e^jwt:

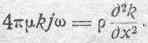
Вводя обозначение:

приведем это уравнение к виду:

' Решение полученного дифференциального уравнения (160) может быть написано в общей форме:

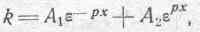
где А ₁и А ₂постоянные интегрирования, определяемые из началь­ных условий. A ₂ должно быть равно нулю, так как если А₂¹ 0, то при удалении исследуемой точки от плоскости раздела внутрь про­водника, т. е. при возрастании координаты х, сила тока должна возрастать беспредельно, что противоречило бы закону сохранения энергии. Следовательно,

А ₂=0

и решение уравнения (160) представится в виде:

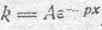(161)

Преобразуем это решение, для чего определим р. По условию:

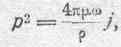
следовательно,

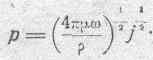
Выражение j ^1/2 представим в ином виде:

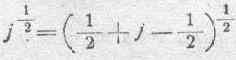
или:

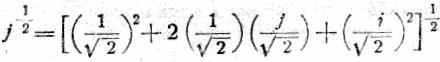
или:

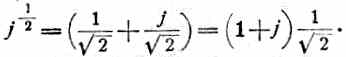
В таком случае выражение для р примет вид:

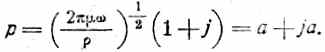
Отсюда имеем для k на основании (161):

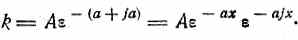
Подставляя полученное решение в выражение для силы тока (159), получим:

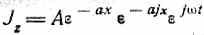
или:

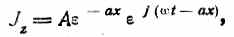
а вспоминая, что реальное значение плотности тока выражается в данном случае вещественной частью комплекса, получим:

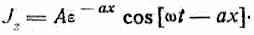
Подставляя сюда значение a:

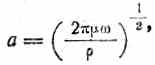
получим окончательно:

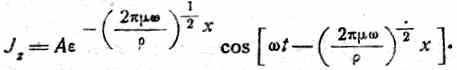(162)

Полученное выражение показывает, что с изменением коорди­наты х меняется и амплитуда и фаза тока. Подставляя значение

х= 0

получим:

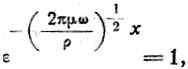
что приводит нас, как и следовало ожидать, к уравнению:

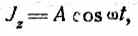
т. е. к выражению для силытока на поверхности раздела.

Нас интересует главным образом амплитуда плотности тока и потому мы в дальнейшем сосредоточим наше внимание исключительно на выражении:

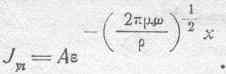
Разберем некоторые конкретные случаи. Остановимся, например, на меди, для которой m=1 и r=1600; подставляем эти данные в выражения для амплитуды при частоте f =100 периодов в се­кунду и, следовательно, при 2 pf =2p•100.

Имеем:

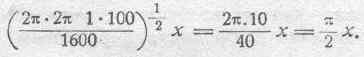
Таким образом, ток пропорционален 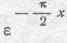. Примем начальные условия такими, чтобы при x= 0, т. е. поверхности раздела, было;

J_m=A= 1.

В таком случае будем иметь:

Если же, например, f =10⁶ периодов в секунду, то получим:

Отсюда вытекает вывод очень важный для техники токов боль­шой частоты: в случае частот порядка миллионов в секунду, прак­тически можно не считаться с токами, циркулирующими в глубине проводника.

Для железа, принимая r=10000 и m=1000, получаем при f =100 следующие результаты:

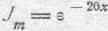
и, следовательно,

Если же принять f =10⁶, то J_m=eps^-2000x и получаем:

В. Томсон (лорд Кельвин) назвал явление, нами рассмотрен­ное, явлением поверхностного эффекта, —skin-effect (skin=шкурка, пленка, слой). Как пример ко всему вышеизложенному, рассмотрим следующее. Предположим, что мы имеем некоторый обычный про­водник. При прохождении по нему переменного тока мы будем наблюдать то же явление skin effect'a, которое выше было матема­тически обследовано для простейшего случая. Благодаря этому, омическое сопротивление проводника переменному току r_a будет больше омического сопротивления току постоянному r_c. Это не­равенство сопротивлений является, как выше было разъяснено, результатом неодинаковой плотности тока в различных слоях про­водника, т. е. тем, что не все части проводника одинаково полно использованы для проведения тока.

Вопрос об увеличении сопротивления проводника при прохожде­нии по нему переменного тока занимал, кроме В. Томсона, еще лорда Рэлея, Ми, Госпиталье и других. Точное математиче­ское решение задачи для случая обычного проводника с круговым сечением приводит к сложным выкладкам, и мы поэтому ограни­чимся только результатами, пригодными для простых вычислений. Приводим выборку из таблицы, составленной Госпиталье для меди на основании расчетов и опытов В. Томсона.

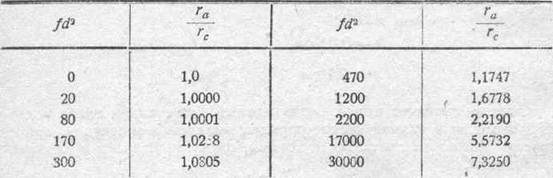
Из таблицы непосредственно видно, как изменяется сопро­тивление медного проводника при изменении его диаметра d или частоты переменного тока /. На практике, в технике низ­ких частот, частота редко превышает 50 — 60 периодов в се­кунду; диаметр проводников обычно сравнительно редко делают более 1—1¹/₂ см. Поэтому величина fd ²обычно не превы­шает 60*1,5²=135. Следовательно, r_a почти не отличается от r_c, Но в области радио, где применяются большие частоты, r_a значи­тельно превосходит r_f Что касается железных проводов, то уже

при низких частотах, вследствие более высокой магнитной проницаемости, происходит значительно большее увеличение сопроти­вления, чем для медных проводов. Учет явления при железных проводах очень осложняется тем, что m непостоянно и, кроме того, сказывается на r_a влияние гистерезиса.

В последние годы в качестве материала для проводов начали употреблять еще алюминий (передача энергии и т.д.). Алюминиевые проводники более выгодны в отношении явления неравномерного распределения тока, чем медные, вследствие того, несомненно, что их проводимость почти вдвое меньше таковой же у медных. Ниже мы даем еще одну таблицу для сравнения процентного увели­чения сопротивления для алюминиевых и медных проводников.

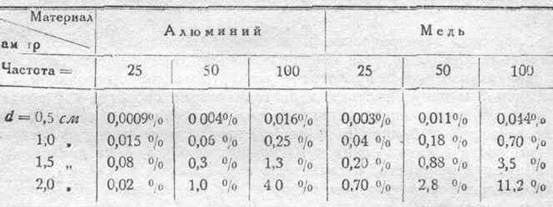
Явление skin-effect'a имеет место между прочим и в проводниках машин переменного тока: в данном случае сопротивление также увеличивается. Необходимо оговориться еще, что там это явление осложняется появлением токов Фуко в проводниках вследствие перемещений проводников в неравномерных полях (причина, почему проводники нередко расслаиваются).

¹) Так как, вообще,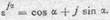

Дата добавления: 2014-11-29