Пойнтинга

Механизм движения электромагнитной энергии. Вектор

Вопрос о механизме распространения электромагнитных воз­мущений и связанного с этим движения электромагнитной энергии представляет глубокий интерес. На этом предмете останавливали свое внимание многие выдающиеся физики. Наиболее законченную и строго продуманную картину процессов, происходящих в электро­магнитном поле, дал Пойнтинг. В своих построениях он исходил из представления о реально существующих фарадеевских трубках. Так как, однако, общая схема его рассуждения и полученные им результаты по существу нисколько не зависят от того, основываемся ли мы на представлении о фарадеевских трубках или на идее о „физических магнитных линиях", как реально существующих элементах магнитного поля, то мы попытаемся в дальнейшем из-

ложить основные мысли Пойнтинга, не приурочивая их специально к той или иной исходной точке зрения, но, по возможности, со­гласуй эти точки зрения между собою, где это окажется вы­полнимым.

Прежде всего скажем несколько слов касательно взаимной ориентировки в электромагнитном поле векторов электрической силы и электрического смещения, с одной стороны, и магнитной силы и магнитной индукции, с другой стороны. По существу эта ориентировка вполне определяется основными дифференциальными уравнениями электромагнитного поля, приведенными в предыдущих параграфах (см. § 121, конец — Е_х и H_y). Очень просто можно также получить интересующий нас результат, если рассмотреть систему прямолинейных магнитных линий, движущихся перпендикулярно самим себе со скоростью V. В таком случае в ка­ждой точке пространства, мимо которой пробегает эта система магнитных линий, должны иметь место электрическая сила Е и электрическое смещение D, которые можно считать следствием явления элек­тромагнитной индукции в данном месте поля, понимаемой с той обобщенной точки зрения, на которую по существу стал Максвелл (§ 59). Таким образом, не трудно путем применения обычных пра­вил получить картину взаимной ориенти­ровки векторов Б, D, H, В и вектора ско­рости v, представленную на рисунке 186.

Рассмотрим теперь вывод, данный Пойнтингом для получения выражения скорости распространения электромагнитных возмущений и общего соотношения между Е, Н и v. При этом мы будем воз­можно ближе, почти дословно держаться подлинника.

Представим себе, что серия плоско-поляризованных электромаг­нитных волн свободно движется в среде, для которой магнитная проницаемость равна m и диэлектрическая постоянная e. Допустим, что эти волны движутся равномерно со скоростью v, не изменяя своей формы. Пусть AECNF (рис. 187) есть серия волн электри­ческого смещения или электрической силы, причем векторы элек­трической силы и смещения расположены в плоскости рисунка и перемещаются слева направо со скоростью v.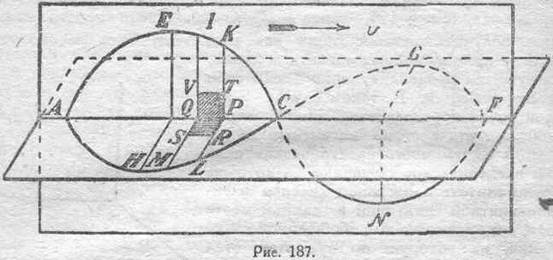

Согласно теории Максвелла всякое изменение электрического смещения сквозь, например, площадку PRSQ эквивалентно, с точки зрения магнит­ных действий, току через эту площадку, и если, как на рисунке 187, электрическое смещение сквозь эту площадку возрастает (снизу вверх), то в контуре, ограничивающем эту поверхность, по-

является магнитодвижущая сила, т. е. в плоскости, перпендикуляр­ной электрической силе, существует магнитное поле. Наоборот, электрическое смещение сквозь поверхность PTVQ, расположенную в плоскости рисунка, всегда равно нулю, и в этой плоскости не имеется составляющей магнитного поля. Таким образом, волны электрические существуют совместно с волнами магнитными, пло­скость которых перпендикулярна первым. Изобразим магнитную волну через AHCQF. Плоскости, соответствующие двум волнам, мы можем назвать плоскостями электрической и магнитной. Предположим, что неподвижная площадка PRSQ изображает один квад­ратный сантиметр магнитной плоскости. Пусть D есть электриче­ское смещение в точке Q и D^f — в точке Р. Пользуясь представ­лением о фарадеевскнх трубках, мы можем сказать, что число этих трубок, покидающих площадку PQSR через сторону PR в од­ну секунду, равно vD'•PR, или vD', а число трубок, входящих в рассматриваемую площадку в течение секунды через противо­положную границу QS, есть vD. Скорость изменения полного электрического смещения сквозь данную площадку является мерою тока смещения сквозь эту площадку и равна v(D-D'). Пусть Н есть магнитная сила в точке Q, а Н' — в точке Р; линейный интег­рал магнитной силы вдоль контура PQSR равен Н-Н'. Таким образом:

H-H'=4pv(D-D'). (148)

Рассмотрим теперь изменение магнитной индукции сквозь пло­щадку PTVQ, находящуюся в электрической плоскости. Пусть В есть магнитная индукция в точке Q и В' — в точке Р. Число еди­ничных трубок магнитной индукции (магнитных линий), покидаю­щих в секунду площадку PTVQ через сторону РТ, равно vB', а число трубок, входящих в PTVQ через сторону QV, равно vB.

Допустим, что площадка PTVQ есть также квадратный санти­метр. Приращение магнитного потока через эту поверхность в еди­ницу времени есть, следовательно, v(B-В') и равно интегралу электрической силы вдоль контура PTVQ, взятому с обратным знаком.

Если Е есть электрическая сила в точке Q и Е'— в точке Р, то имеем:

E-E'=v(B-B'). (149)

Перемножая почленно (148) и (149) и пользуясь соотношениями

получим:

откуда приходим к известному соотношению (143);

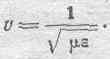
Таким образом, в соответствии с вышесказанным, можно фор­мально рассматривать магнитную силу вдоль QS, как следствие пересечения этой линии трубками электрического смещения или, обратно, а электрическую силу вдоль QV какследствие пересече­ния этой линии трубками магнитной индукции; в действительности же, конечно, мы имеем дело с единым, неделимым электромаг­нитным комплексом, отдельные стороны которого мы характери­зуем векторами D и В.

Если вместо того, чтобы рассматривать площадку в 1 квадрат­ный сантиметр, взять полоску шириною в 1 см, один конец кото­рой находится в Q, а другой настолько удален, что электромагнит­ное смещение еще не достигло этого достаточно удаленного района, то очевидно имеем:

формулы, которые дают наиболее отчетливо соотношение между электрической силой и магнитной силой, рассматриваемыми, как органически связанные между собою характеристики единого элек­тромагнитного поля.

Переходим теперь к вопросу о движении энергии в электромаг­нитном поле.

Согласно теории Максвелла количество энергии, рассчитанной на кубический сантиметр, соответствующее наличию электрической деформации среды, равно в точке Р:

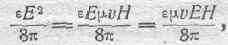
а соответствующее количество энергии, определяемое наличием магнитного поля в той же точке Р равно:

т. е. энергии электрическая и магнитная равны в каждом эле­менте объема электромагнитного поля при условии, что Е и Н свя-

заны друг с другом соотношениями (150) и (151), характеризую­щими случай свободного распространения электромагнитной энер­гии. Полное количество энергии, приходящийся на кубический сантиметр, равно, следовательно:

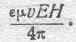
Если мы предположим теперь, что эта энергия равномерным потоком перемещается со скоростью v, то количество энергии, которое в течение одной секунды может быть поглощено одним квадратным сантиметром поверхности, перпендикулярной к направ­лению этого потока электромагнитной энергии, равно:

Так как в случае свободного распространения электромагнитной энергии v²me=1, то полученное выражение может быть переписано так:

Выражение EH/4pi, представляющее собою мощность потока электро­магнитной энергии, рассчитанную на единицу поверхности попе­речного сечения этого потока, принято обозначать буквою S.

Представляют большой интерес общие соображения, высказы­ваемые самим Пойнтингом по поводу соотношения (152). Ниже мы приводим их дословно:

„Вид этого выражения для количества переносимой, энергии, которое является величиной, характеризующей действие одной части среды на соседние, подсказывает мысль, что оно представляет собою общий закон для случая, когда электрическая и магнитная силы взаимно перпендикулярны. Мы можем, с известной долей правдоподобия, рассматривать электрическую силу как нечто ана­логичное силе упругости, а магнитную индукцию — как нечто аналогичное скорости. Для передачи механической энергии необхо­димо одновременное существование силы и скорости, и количество переданной энергии зависит от произведения этих двух величин. Если предыдущая аналогия имеет основания, то мы можем принять, что количество перенесенной электромагнитной энергии зависит от произ­ведения электрической силы и магнитной силы, что вполне соответ­ствует полученным выше результатам. Заметим, что энергия распрост­раняется в направлении, перпендикулярном плоскости, в которой находятся обе силы; это направление получается из направления Н поворотом вправо вокруг Е, как оси".

Правило, данное Пойнтингом и приведенное в последних строках, можно формулировать еще следующим образом (см. рис. 186). Вектор S, который называется обычно вектором Пойнтинга, имеет направление, совпадающее с направлением поступательного

движения винта штопора, рукоятка которого вращается в плоскости, содержащей Е и H, в направлении от Е к Н (рис. 188).

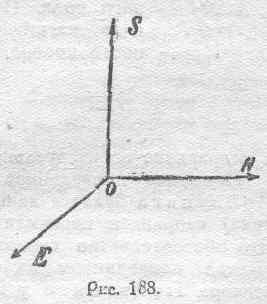
Как мы уже отмечали выше, движение энергии имеет место только в том случае, если Е к Н являются величинами взаимно связанными, т. е. являются характеристиками одного и того же электрокинетического процесса. Только в этом случае имеет смысл указанное геометрическое и численное соотношение между векто­рами Е, Н и S.

Укажем еще, что в случае, когда E и H не перпендикулярны друг к другу, указанное соотношение принимает более сложный вид:

где q есть угол между направлениями векторов Е и Н.

Пойнтинг дал весьма простой вышеприведенный вывод со­отношения (152):

исходя из определенного представления о механизме распростра­нения электромагнитной энергии. Однако, справедливость этого соотношения не зависит от той карти­ны механизма явления, которую Пойнтинг положил в основу своего упро­щенного вывода. Эта картина является более или менее достоверной рабочей гипотезой, тогда как величина вектора Пойнтингa S, характеризующего мощ­ность потока электромагнитной энер­гии, может быть чисто формальным математическим путем получена и из основных уравнений Максвелла, что в свое время было сделано самим Пойнтингом.

Замечательно, что даже в случаях несвободного распространения электромагнитной энергии, когда соотношения (150) и (151) утрачи­вают свою полную силу, вектор Пойнтинга все же сохра­няет физический смысл и может быть применяем для характери­стики мощности потока электромагнитной энергии. Пример несво­бодного распространения этой энергии мы имеем,между прочим, в пространстве, окружающем проводник цепи постоянного тока. Но и в этом случае вполне уместно пользоваться вектором Пойнтинга при рассмотрении энергетической стороны процессов, протекающих в цепи. Для иллюстрации сказанного остановимся на простейшем подобном примере.

Допустим, что имеется некоторый участок прямолинейного про­водника, играющего роль приемника электромагнитной энергии

и преобразующего ее в тепло. Предположим, что по этому провод­нику идет постоянный ток. Определим величины и направления Е, Н и S для данного случая.

Пусть проводник (рис. 189) имеет форму кругового цилиндра ра­диуса а, длина рассматриваемого участка есть l и сопротивление этого участка r.

Если i —сила тока, проходящего по проводнику, то ri выражает падение напряжения на рассматриваемом участке проводника, а отношение:

ri/l

есть падение напряжения на единицу длины, т. е. это есть сила электрического поля вдоль проводника. Та­ким образом, можем положить для точек вблизи самой поверхности проводника:

E=ri/l

причем Е будет направлено парал­лельно оси проводника.

Обратимся теперь к силе магнит­ного поля. По закону Био-Савара, сила магнитного поля на поверх­ности проводника равна

и направлена по касательной к нормальному сечению проводника. Применяя приведенное выше правило, убедимся, что вектор Пойнтинга будет в данном случае (у самой поверхности провод­ника) направлен перпендикулярно к оси проводника (рис. 190).

Это обстоятельство свидетельствует о том, что энергия погло­щается проводником из окружающего пространства. Величину вектора Пойнтинга у поверхности проводника, т. е. количество энергии, проникающее в проводник в одну секунду через каждый квадратный сантиметр его поверхности, получим, составив выраже­ние:

На основании предыдущего имеем:

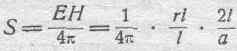
или

Так как боковая поверхность рассматриваемого участка про­водника равна 2pi al, то полное количество энергии, поглощаемое рассматриваемым участком в одну секунду, т. е. поглощаемая им мощность, будет

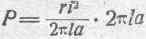
или

р=ri².

Таким образом, пользуясь вектором Пойнтинга, мы полу­чаем то же выражение для мощности, поглощаемой проводником, которое дают и другие общеизвестные соотношения.

Попутно мы получили здесь иллюстрацию того утверждения, что энергия, которая в форме тепла выделяется в проводнике, вхо­дит в объем этого проводника из окружающего его диэлектрика, а не передается внутри проводника через его поперечные сечения,

В случае так называемой передачи энергии по проводам, неза­висимо от того, являются ли проводники элементами собственно линии передачи или частью приемной цепи, преобразующей элек­тромагнитную энергию в тепло, эта энергия движется от генера­тора по диэлектрику, причем проводники играют роль направляю­щей потока электромагнитной энергии, которая в большей или меньшей степени извне проникает в вещество проводников, преобразуясь там в тепло. Таким образом, вообще говоря, вектор Пойнтннга имеет составляющую параллельную оси провода, характеризующую поток электромагнитной энергии, движущийся вдоль провода по направлению к приемникам, и составляющую перпендикулярную оси провода, характеризующую ту часть потока энергии, которая, как было разъяснено выше, превращается в тепло в веществе проводника: В случае излучения энергии от антенны радиоустановки в каждой точке окружающего пространства вектор Пойнтинга в точности определяет величину и направление мощ­ности потока электромагнитной энергии.

Дата добавления: 2014-11-29