Модуль кручения

При закручивании стержня вокруг его оси возникающая деформация является неоднородной деформацией сдвига. Это делается очевидным, если мысленно разбить стержень на ряд коаксиальных полых цилиндров. Угол сдвига g одного такого полого цилиндра (внутренним радиусом r и толщиной стенки dr) связан с углом закручивания j очевидным соотношением (см. рис. П1):

rj=Lg,

откуда

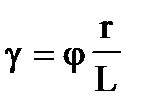(П1).

Полученное соотношение показывает, что сдвиг является неоднородным, т.к. угол сдвига g зависит от расстояния до оси r.

Деформация стержня приводит к возникновению упругих сил в стержне, момент которых нетрудно вычислить. Согласно закону Гука напряжение s при сдвиге связано с углом сдвига g и модулем сдвига G соотношением:

s = –Gg (П2).

Поэтому момент упругих сил (момент вычисляется относительно оси цилиндра), возникающих в рассматриваемом цилиндре, равен:

dM = –s×r×dS (П3),

где dS=2pr×dr - площадь поперечного сечения цилиндра.

С учетом (П1) и (П2) dM запишется в виде:

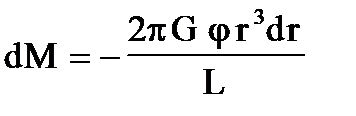(П4).

Интегрируя (П4) по dr получим:

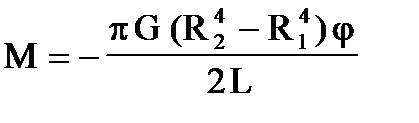(П5).

В (П5) R₁ и R₂ - пределы интегрирования по dr. Для сплошного стержня R₁=0, R₂ – радиус стержня. В случае трубы R₁ и R₂ - внутренний и внешний радиусы трубы, соответственно. Заметим, что момент очень быстро возрастает с ростом внешнего радиуса R₂ (M~R⁴). Это позволяет использовать трубы вместо стержней практически не теряя в прочности конструкции. Действительно, даже если R₂/R₁=1,5, то (R₂/R₁)⁴»6, и такая труба будет менее жесткой, чем сплошной стержень всего на 15%, масса же такой трубы будет приблизительно вдвое меньше, чем у сплошного стержня.

Коэффициент перед (в (П5) называется модулем кручения:

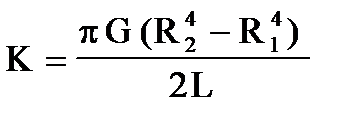(П6).

В нашем опыте мы используем проволоку, поэтому (П6) принимает вид:

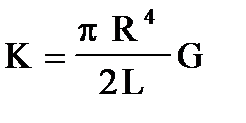(П7).

Рассмотрим тело с моментом инерции I, подвешенное на проволоке с модулем кручения K. Если телу сообщить вращение вокруг оси на угол j, то это приведет к возникновению в проволоке упругих сил с моментом

M = –Kj.

Запишем уравнение моментов для тела:

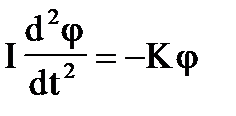(П8).

Поделив обе стороны этого уравнения ни I, придем к уравнению гармонических колебаний:

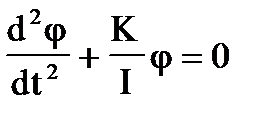(П9).

Квадрат частоты колебаний, как известно, дается коэффициентом перед j:

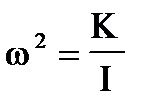(П10).

С учетом равенства (П7), получаем для периода колебаний T=2p/w:

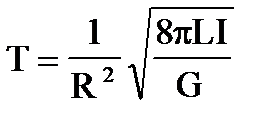(П11).

Дата добавления: 2014-11-29