Методы регрессионного и корреляционного анализа

Регрессионный анализ используется для исследования форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого случайного процесса. Иными словами связь между случайной и неслучайной величинами называется регрессионной, а метод анализа – регрессионным анализом.

Уравнение регрессии в теории корреляции используется для решения задачи прогнозирования изменений случайной величины 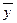по данным эксперимента или наблюдениям x₁, x₂, x₃ …x_n. Точность прогноза оценивается средней из условий дисперсии. Простейшей функцией регрессии является линейная.

Корреляционный анализ изучает корреляцию связи между случайными величинами. Две случайные величины a и b называют корреляционно связанными, если математическое ожидание одной из них меняется в зависимости от изменения другой. Теснота связи между случайными величинами a и b характеризуется (при соблюдении некоторых предпосылок) коэффициентом корреляции z(a, b). Если z(a, b) = 0, то это говорит о том, что величины a и b не коррелируются. Если z(a, b) = 1, то имеется прямая функциональная зависимость.

Корреляционный анализ позволяет количественно оценить связи между большим числом взаимодействующих явлений (экономических). Его изменение делает возможным проверку различных экономических гипотез о наличии и силе связи между двумя явлениями и группой явлений. Корреляционный анализ тесно связан с регрессионным.

Регрессионный анализ предполагает решение двух задач. Первая заключается в выборе независимых переменных, существенно влияющих на зависимую величину, и определении формы управления регрессии (этап – спецификации). Данная задача решается путем анализа изучаемой взаимозависимости по существу. Формальные средства могут служить здесь лишь некоторыми ориентирами. Вторая задача – оценка параметров – решается с помощью того или иного статистического метода обработки наблюдения.

Применение корреляционного анализа предполагает реализацию следующих предпосылок: определение тесноты и формы связи переменных зависимостей, при этом существенна задача исследования формы связи. Выбор тех или иных показателей тесноты корреляционной зависимости определяются ее формой. Кроме того, никакой прогноз относительно дальнейшего развития изучаемого явления в его связи с данным фактором невозможен без представления о форме этой связи. Под формой корреляционной зависимости понимают ту тенденцию, которая проявляется в изменении изучаемого признака в связи с изменением признака-фактора.

Дата добавления: 2014-11-29