Входные и выходные данные 2 страница

Вывод - перебор следует выполнять не по всем жителям и не для всех партий! Если бы это выручало всегда. Сверхактивность жителей сводит на нет этот путь сокращения перебора. Остается надеяться, что кто-то должен и выращивать хлеб, а не только митинговать. Итак, “набросок” общей логики предварительной обработки.

...

while <есть вхождения> do begin

<исключить менее активных жителей>;

<сжать А>;

<для “карликовых” партий включить жителей, представляющих их, в состав парламента>;

<изменить значения величин, описывающих процесс формирования парламента (Res, Rt, mn, Rwork)>;

<откорректировать A>;

end;

...

Заметим, что необходимо исключить партии, “покрытые” жителями, представляющими карликовые партии из А[i].part оставшихся жителей. Это может привести к тому, что возможно появление жителей, представляющих все оставшиеся партии. Совместим проверку наличия вхождений, исключение части жителей и сжатие массива A в одной функции. Ее вид.

function Come(var t:Nint):boolean; {Проверяем - есть ли вхождения? Если есть, то исключаем соответствующих жителей и сжимаем массив А}

var i,j,l:Nint;

begin

for i:=1 to t-1 do

for j:=i+1 to t do if A[j].part<=A[i].part then begin

A[j].part:=[];A[j].number:=0;

end;

l:=t;

for i:=1 to t do begin

if (A[i].part=[]) and (i<=l) then begin for j:=i to l-1 do A[j]:=A[j+1];

A[l].number:=0;A[l].part:=[];

Dec(l);

end;

end;

Come:=Not(t=l);

t:=l;

end;

Вариант построения процедуры исключения «карликовых» партий может быть и таким.

procedure Pygmy(t:Nint;var r,p:Sset);{t - количество обрабатываемых элементов массива А; r - множество номеров жителей, включаемых в парламент; p - множество номеров партий, представляемых жителями, включенных в парламент}

var i,j:Nint;v:Sset;

begin

r:=[];p:=[];

for i:=1 to t do begin

{определяем множество партий представляемых всеми жителями кроме A[i].man}

v:=[];

for j:=1 to t do if i<>j then v:=v+A[j].part;

{если есть хотя бы одна партия, которую представляет только житель с номером A[i].man, то этого жителя мы обязаны включить в парламент}

if A[i].part*v<>A[i].Part then r:=r+[A[i].man];

end;

{формируем множество партий, имеющих представительство в данном составе парламента}

for i:=1 to t do if A[i].man in r then p:=p+A[i].part;

end;

Итак, фрагмент предварительной обработки (до перебора).

....

t:=N;Rt:=[1..N];Rwork:=[];

One(t,Rt);

while Come(t) and (Rt<>[]) do begin Rg:=[];Rp:=[];

Pygmy(t,Rg,Rp);

Rt:=Rt-Rp;Rwork:=Rwork+Rg;

if Rp<>[] then begin

for i:=1 to t do begin{исключение}

for j:=1 to N do

if (j in Rp) and (j in A[i].part) then A[i]part:=A[i].part-[j];

A[i].number:=Num(A[i].part);

end;

<сортировка А>;

end;

end;

if (Rt<>[]) then One(t,Rt);

Блок общих отсечений. Подсчитаем для каждого значения i (1£i£t) множество партий, представляемых жителями, номера которых записаны в элементах массива с i по t (массив С:array[1..N] of Sset). Тогда, если Res - текущее решение, а Rt - множество партий, требующих представления, то при Res+C[i]£Rt решение не может быть получено и эту ветку перебора следует “отсечь”.

Формирование массива С.

C[t]:=A[t].part; for i:=t-1 downto 1 do begin

C[i]:=[];C[i]:=A[i].part+C[i+1];

end;

Блок отсечений по i. Если при включении элемента с номером i в решение, значение величины Rt не изменяется, то это включение бессмысленно (A[i].part*Rt=[]).

На этом мы закончим обсуждение этой, очень интересной с методической точки зрения, задачи. Заметим, что для любой вновь возникающей идеи по сокращению перебора место для ее реализации в логике определено. А именно, предобработка, общие отсечения, покомпонентные отсечения - другого не дано.

Примечание. Графовая модель задачи (двудольный граф). Каждому жителю соответствует вершина в множестве X, каждой партии - вершина в множестве Y. Ребро (i,j) существует, если житель с номером i представляет партию с номером j. Требуется найти минимальное по мощности множество вершин S, такое, что SÍX и для любой вершины jÎY существует вершина iÎS, из которой выходит ребро в вершину j. Модификация задачи о нахождении минимального доминирующего множества.

Постановка задачи. В рюкзак загружаются предметы n различных типов (количество предметов каждого типа не ограничено). Максимальный вес рюкзака W. Каждый предмет типа i имеет вес w_i и стоимость v_i (i=1,2,..., n). Требуется определить максимальную стоимость груза, вес которого не превышает W. Обозначим количество предметов типа i через k_i, тогда требуется максимизировать v₁*k₁+v₂*k₂+...+v_n*k_n при ограничениях w₁*k₁+w₂*k₂+...+w_n*k_n£W, где k_i - целые (0£k_i£[W/w_i]), квадратные скобки означают целую часть числа.

Рассмотрим простой переборный вариант решения задачи, работоспособный только для небольших значений n (определить, для каких?). Итак, данные:

Сonst MaxN=????;

Var n,w:integer;{количество предметов, максимальный вес}

Weight,Price:array[1..MaxN] of integer;{вес, стоимость предметов}

Best,Now:array[1..MaxN] of integer;{наилучшее, текущее решения}

MaxPrice:LongInt;{наибольшая стоимость}

Решение, его основная часть - процедура перебора:

Procedure Rec(k,w:integer;st:LongInt);

{k - порядковый номер группы предметов, w - вес, который следует набрать из оставшихся предметов, st - стоимость текущего решения}

var i:integer;

begin

if (k>n) and (st>MaxPrice) then begin {найдено решение}

Best:=Now;MaxPrice:=st; end

else if k<=n then

for i:=0 to w div Weight[k] do begin

Now[k]:=i;

Rec(k+1,W-i*Weight[k],st+i*Price[k]);

end;

end;

Инициализация переменных, вывод решения и вызывающая часть (Rec(1,w,0)) очевидны. В данной логике отсутствуют блоки предварительной обработки, общих отсечений и отсечений по номеру предмета (смотрите задачу о парламенте). В блоке предварительной обработки целесообразно найти какое-то решение, лучше, если оно будет как можно ближе к оптимальному (наилучший вариант загрузки рюкзака). «Жадная» логика дает первое приближение. Кроме того, разумно выполнить сортировку, например, по значению стоимости предметов или отношению веса предмета к его стоимости. Построение блока общих отсечений аналогично тому, как это сделано в задаче о парламенте, а ответ на вопрос, почему предметы данного типа не стоит складывать в рюкзак, остается открытым.

Постановка задачи. Классическая формулировка задачи известна уже более 200 лет: имеются n городов, расстояния между которыми заданы; коммивояжеру необходимо выйти из какого-то города, посетить остальные n-1 городов точно по одному разу и вернуться в исходный город. При этом маршрут коммивояжера должен быть минимальной длины (стоимости).

Задача коммивояжера принадлежит классу NP-полных, то есть неизвестны полиномиальные алгоритмы ее решения. В задаче с n городами необходимо рассмотреть (n-1)! маршрутов, чтобы выбрать маршрут минимальной длины. Итак, при больших значениях n невозможно за разумное время получить результат.

Перебор вариантов. Оказывается, что и при простом переборе не обязательно просматривать все варианты. Это реализуется в данном классическом методе.

Структуры данных.

Const Max=100;

Var A:array[1..Max,1..Max] of integer;{Матрица расстояний между городами}

B:array[1..Max,1..Max] of byte;{Вспомогательный массив, элементы каждой строки матрицы сортируются в порядке возрастания, но сами элементы не переставляются, а изменяются в матрице В номера столбцов матрицы А }

Way, BestWay:array[1..Max] of byte;{Хранится текущее решение и лучшее решение}

Nnew:array[1..Max] of boolean;{Значение элемента массива false говорит о том, что в соответствующем городе коммивояжер уже побывал}

BestCost:integer;{Стоимость лучшего решения}

Идея решения. Пусть мы находимся в городе с номером v. Наши действия.

Шаг 1. Если расстояние (стоимость), пройденное коммивояжером до города с номером v, не меньше стоимости найденного ранее наилучшего решения (BestCost), то следует выйти из данной ветви дерева перебора.

Шаг 2. Если рассматривается последний город маршрута (осталось только вернуться в первый город), то следует сравнить стоимость найденного нового решения со стоимостью лучшего из ранее найденных. Если результат сравнения положительный, то значения BestCost и BestWay следует изменить и выйти из этой ветви дерева перебора.

Шаг 3. Пометить город с номером v как рассмотренный, записать этот номер по значению Count в массив Way.

Шаг 4. Рассмотреть пути коммивояжера из города v в ранее не рассмотренные города. Если такие города есть, то перейти на эту же логику с измененными значениями v, Count, Cost, иначе на следующий шаг.

Шаг 5. Пометить город v как нерассмотренный и выйти из данной ветви дерева перебора.

Пример. Ниже приведены матрицы А и В (после сортировки элементов каждой строки матрицы А).

Примечание. Можно использовать любой из методов сортировки, но авторы предпочитают использовать метод Хоара[1] из-за определенного изящества в его реализации. Рекурсивная логика плюс смена направления изменения индекса в одной циклической конструкции.

A B

@
	@
		@
			@
				@
					@

Примечание. Символом @ обозначено бесконечное расстояние.

Прежде чем перейти к обсуждению логики, целесообразно разобрать этот перебор на примере. На рисунке приведен пример и порядок просмотра городов. В кружках указаны номера городов, рядом с кружками - суммарная стоимость проезда до этого города из первого.

Итак, запись логики.

procedure Solve(v,Count:byte;Cost:integer);

{v - номер текущего города; Count - счетчик числа пройденных городов; Cost - стоимость текущего решения}

var i:integer;

begin

if Cost>BestCost then exit;{Стоимость текущего решения превышает стоимость лучшего из ранее полученных }

if Count=N then begin Cost:=Cost+A[v,1];Way[N]:=v;{Последний город пути. Доформировываем решение и сравниваем его с лучшим из ранее полученных.}

if Cost<BestCost then begin

BestCost:=Cost;BestWay:=Way;

end;

exit;

end;

Nnew[v]:=false;Way[Count]:=v;{Город с номером v пройден, записываем его номер в путь коммивояжера}

for i:=1 to N do if Nnew[B[v,i]] then

Solve(B[v,i], Count+1,Cost+A[v,B[v,i]]); {Поиск города, в который коммивояжер может пойти из города с номером v}

Nnew[v]:=true; {Возвращаем город с номером v в число непройденных}

end;

Первый вызов - Solve(1,1,0).

Разработка по данному «шаблону» работоспособной программы - техническая работа. Если Вы решитесь на это, то есть смысл проверить ее работоспособность на следующем примере (матрица А приведена ниже). Решение имеет вид 1 8 9 2 5 10 6 7 4 3 1, его стоимость 158.

@
	@
		@
			@
				@
					@
						@
							@
								@
									@

Оцените время работы программы. Если у Вас мощный компьютер, то создайте матрицу А[1..50,1..50] и попытайтесь найти наилучшее решение с помощью разобранного метода. Заметим, что набор 2500 чисел - утомительное занятие и разумная лень - «двигатель прогресса».

Задан круг, разделенный на секторы. Даны три числа: k (0<=k<=20), n (n<=6) и m (m<=20), где n - количество секторов. В каждый из секторов помещается одно число >= k. Когда секторы заполнены числами, Вы можете получать из них новые числа по одному из следующих правил:

· взять число из одного сектора;

· взять число, равное сумме двух или более чисел в смежных секторах.

Из этих чисел составляется наибольшая последовательность подряд идущих новых чисел, начинающихся с числа m:(m, m+1, m+2,..., i).

Напишите программу, которая определяет способ расстановки чисел в секторах, максимизирующий длину последовательности.

Пример. На рисунке показано, как получаются все новые числа от 2 до 21 из чисел, записанных в секторах. Серым цветом выделены суммируемые числа.

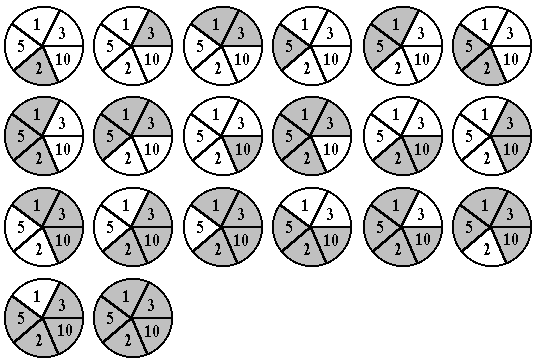
Исходные данные расположены во входном файле с именем INPUT.TXT, который содержит числа n, m и k. Ниже приведен пример файла исходных данных INPUT.TXT.

Выходной файл с именем OUTPUT.TXT должен содержать:

· наибольшее число i в неразрывной последовательности, которое может быть получено из чисел в секторах;

· все наборы чисел в секторах, из которых можно получить неразрывную последовательность от m до i. В каждой строке выводится один набор чисел в секторах. Каждый такой набор - список чисел, начинающихся с наименьшего (которое может быть не единственным).

Например, (2 10 3 1 5) не является решением, так как начинается не с наименьшего числа. Обратите внимание, что (1 3 10 2 5) и (1 5 2 10 3) считаются различными решениями и должны быть оба выведены. Ниже приведен файл OUTPUT.TXT для нашего примера.

1 3 10 2 5

1 5 2 10 3

2 4 9 3 5

2 5 3 9 4

Если наименьшее число встретится несколько раз, вывести все возможные комбинации, например: (1 1 2 3), (1 2 3 1), (1 3 2 1) и (1 1 3 2).

Рассуждения по поводу задачи. Очевидно, что в первый сектор может помещаться число из интервала от k до m. Считаем, что минимальное из чисел находится в первом секторе. Если k больше m, то задача не имеет решения. Обозначим через Up верхнюю границу, а через Down - нижнюю границу интервала, из которого могут браться числа для записи в сектора с номерами от 2 до n. Общая схема («набросок»).

for l:=k to m do begin

<выбор числа в первый сектор>;

for j:=2 to n do begin (* j - номер сектора *)

<определение значений верхней и нижней границ для чисел, записываемых в сектор с номером j>;

for i:=Down to Up do (* i - записываемое число *)

begin

< записать в сектор с номером j число i >

< откорректировать массив сумм, которые можно составить из чисел, записанных в сектора>

< выполнить проверку последовательности сумм >

end;

end;

end;

Эта привлекательная схема перебора мало пригодна для «жизни», ибо время перебора будет весьма не привлекательным. Попробуем на этапе уточнения повысить пригодность схемы. "Откорректировать массив сумм". Пусть в Q (array[1..n,0..n] of byte) будут храниться суммы чисел из секторов круга S (array[1..n] of byte). В нулевом столбце элементы равны 0. В 1-м столбце - суммы, составленные из чисел, взятых из одного сектора, 2-м - из двух и т.д. В n-м столбце подсчитывается только элемент в первой строке.

Массив Q:

		S[1]	Q[1,1]+S[2]	Q[1,2]+S[3]	Q[1,3]+S[4]	Q[1,4]+S[5]	Q[1,5]+S[6]
		S[2]	Q[2,1]+S[3]	Q[2,2]+S[4]	Q[2,3]+S[5]	Q[2,4]+S[6]
		S[3]	Q[3,1]+S[4]	Q[3,2]+S[5]	Q[3,3]+S[6]	Q[3,4]+S[1]
		S[4]	Q[4,1]+S[5]	Q[4,2]+S[6]	Q[4,3]+S[1]	Q[4,4]+S[2]
		S[5]	Q[5,1]+S[6]	Q[5,2]+S[1]	Q[5,3]+S[2]	Q[5,4]+S[3]
		S[6]	Q[6,1]+S[1]	Q[6,2]+S[2]	Q[6,3]+S[3]	Q[6,4]+S[4]

Итак, если у нас есть массив констант (для простоты) Sq вида

1 2 3 4 5 6 2 3 4 5 6 0 3 4 5 6 1 0 5 6 1 2 3 0 6 1 2 3 4 0,

то элемент массива Q[i,j] вычисляется следующим образом: Q[i,j]:=Q[i,j-1] + Q[Sq[i,j],1].

При изменении числа в секторе с номером t необходимо откорректировать часть матрицы Q, показанную на рисунке темным цветом (эта часть больше, чем требуется, но для простоты считаем ее такой).

Схема процедуры уточнения сумм:

procedure AddSum(t,number:byte);

(* Q, Sq - глобальные переменные *)

var z,i,j:integer;

begin

Q[t,1]:=number;

for i:=1 to n do begin

if t-i+1>1 then z:=t-i+1 else z:=2;

for j:=z to n-1 do begin

Q[i,j]:=0;

Q[i,j]:=Q[i,j-1]+Q[Sq[i,j],1];

end;

end;

Q[1,n]:=Q[1,5] + Q[n,1];

end;

Следующее уточнение. "Выполнить проверку последовательности сумм". Из чего следует исходить? Во-первых, наилучшая последовательность сумм может получиться не из одного варианта заполнения секторов числами. Поэтому необходимо ввести структуру данных - двумерный массив - для их хранения и, соответственно, указатель числа записанных вариантов:

,

где type SView = array[1..nMax] of byte;

NumS:byte;

Во-вторых, для хранения наибольшего числа необходима переменная MaxS. В-третьих, значения сумм лучше представить множественным типом данных SetS:set of byte. Это упростит логику поиска последовательности. Процедура проверки имеет вид:

procedure Check;

(* SetS, BestS, NumS, MaxS, M - глобальные *)

var i,j:integer;

begin

SetS:=[];

for i:=1 to N do

for j:=1 to N-1 do SetS:=Sets+[Q[i,j]];

SetS:=SetS+[Q[1,N]];

i:=M;

while i in SetS do Inc(i);

if i>MaxS then begin

NumS:=1;

BestS[NumS]:=S;

MaxS:=i;(* на единицу больше действительной длины *)

end

else if i=MaxS then begin Inc(NumS); BestS[NumS]:=S; end;

end;

Общая схема уточнена. Но если довести ее до программы, то решение, например, для исходных данных n=6, m=1, k=1 за реальное время не будет получено. Необходимо сокращать перебор, искать эвристики, позволяющие сделать это.

1-я эвристика. Пусть у нас есть (n-1) сектор, в которые записаны числа, образующие последовательность m, m+1,.... количество сумм (арифметическая прогрессия) равно n*(n-1)div2, т. е. это количество различных чисел, получаемое из чисел в заполненных n-1 секторе. Обозначим через X первое число из последовательности m, m+1,..., которое мы не можем получить. В пустой сектор не имеет смысла записывать число, большее X. Поскольку X не превосходит n(n-1) div 2 + m, то это выражение можно считать значением верхней границы Up чисел, записываемых в сектора. В качестве нижней границы Down следует брать S[1], ибо числа, записываемые в сектора 2, 3,..., n не меньше этого числа.

2-я эвристика. Пусть m<2*k. Тогда числа m, m+1,..., 2*k-1 как сумма чисел из нескольких (более одного) секторов. Следовательно, либо, если 2*k-m£n, все они должны находиться в круге, либо, если 2*k-m>n, в круге должны находиться числа m, m+1,..., m+n-1.

3-я эвристика. "Исключение симметричных решений". При поиске числа для записи в последний сектор значение Down можно уточнить:

if < сектор последний > then Down:=S[2]

else Down:=S[1];

4-я эвристика. "Отсечение снизу". При поиске числа для последнего сектора нам известна максимальная сумма, которую дают числа, записанные в (N-1) сектор. Это значение Q[1,N-1]. Если сумма Up и Q[i,N-1] меньше ранее полученного наибольшего числа MaxS, то эту "ветку" в переборе вариантов можно "отсечь"(при любом варианте заполнения последнего сектора лучшего решения мы не получим).

Описанных эвристик (чем не эвристическое программирование?) оказывается достаточно для написания работоспособной программы для нижеприведенных тестов. В таблице приведены и правильные результаты.

N	M	K	max	1 2 4; 1 4 2
				2 3 4 6; 2 6 4 3
				3 5 7 4 6; 3 6 4 7 5
				1 16 2 20; 1 20 2 16; 1 16 4 18; 1 18 4 16; 2 16 4 17; 2 17 4 16
				16 17 18 19 20; 16 20 19 18 17; 16 17 18 20 19; 16 19 20 18 17; 16 17 19 18 20; 16 20 18 19 17; 16 17 19 18 20; 16 20 18 19 17; 16 17 19 20 18; 16 18 20 19 17; 16 17 20 18 19; 16 19 18 20 17 ...
				1 2 5 4 6 13; 1 13 6 4 5 2; 1 2 7 4 12 5; 1 5 12 4 7 2; 1 3 2 7 8 10; 1 10 8 7 2 3; 1 3 6 2 5 14; 1 14 5 2 6 3; 1 7 3 2 4 14; 1 14 4 2 3 7
				2 3 7 4 9 6; 2 6 9 4 7 3
				4 4 6 5 7 9; 4 9 7 5 6 4; 4 4 9 7 5 6; 4 6 5 7 9 4; 4 5 5 6 7 8; 4 8 7 6 5 5

Дата добавления: 2014-11-28