Решето Эратосфена

Задача о паркете

Задача о рюкзаке (динамическая схема)

Рассмотрим задачу из пункта 1.1.6. Напомним ее формулировку. В рюкзак загружаются предметы n различных типов (количество предметов каждого типа не ограничено). Максимальный вес рюкзака не превышает W. Каждый предмет типа i имеет вес w_i и стоимость v_i (i=1,2,..., n). Требуется определить максимальную стоимость груза, вес которого не превышает W. Обозначим количество предметов типа i через k_i, тогда требуется максимизировать v₁*k₁+v₂*k₂+...+v_n*k_n при ограничениях w₁*k₁+w₂*k₂+...+w_n*k_n£W, где k_i - целые (0£k_i£[W/w_i]), квадратные скобки означают целую часть числа.

Пусть вес рюкзака должен быть равен W. Формализуем задачу следующим образом.

· Шаг i ставится в соответствие типу предмета i=1,2,...,n.

· Состояние y_i на шаге i выражает суммарный вес предметов, решение о загрузке которых принято на шагах 0,1,...,i. При этом y_n=W, y_i=0,1,...,W при i=1,2,...,n-1.

· Варианты решения k_i на шаге i описываются количеством предметов типа i, 0£k_i£ëW/w_iû.

Рассмотрим пример. W=6, и дано четыре предмета

i	wi	vi

Схема работы для данного примера приведена на рисунке. В кружочках выделены только достижимые состояния (суммарные веса для каждого шага в соответствии с приведенной выше формализацией) на каждом шаге. В круглых скобках указаны стоимости соответствующих выборов, в квадратных скобках - максимальная стоимость данного заполнения рюкзака. «Жирными» линиями выделен способ наилучшей загрузки рюкзака.

Текст решения.

Const MaxN=???;

MaxK=???;

Type Thing=Record W,V:Word; end;

Var A:array[1..MaxN,0..MaxK] of word;

P:array[1..MaxN] of Thing;

Old,NewA:array[0..MaxK] of longint;

N,W:integer;

...

procedure Solve;

var k,i,j:integer;

begin

fillchar(Old,sizeof(Old),0);

for k:=1 to N do begin{цикл по шагам}

fillchar(NewA,sizeof(NewA),0);

for i:=0 to W do {цикл по состояниям шага}

for j:=0 to i div P[k].W do {цикл по вариантам решения - количеству предметов каждого вида}

if j*P[k].V+Old[i-j*P[k].W]>=NewA[i] then begin

NewA[i]:=j*P[k].V+Old[i-j*P[k].W];

A[k,i]:=j;{ здесь j количество предметов?}

end;

Old:=NewA;

end;

end;

Вывод наилучшего решения.

procedure OutWay(k,l:integer);

begin

if k=0 then exit

else begin

OutWay(k-1,l-A[k,l]*P[k].V);{ а здесь вес }

Write(A[k,l],’ ‘);

end;

end;

Первый вызов - OutWay(N,W). Эту схему реализации принято называть «прямой прогонкой». Ее можно изменить. Пусть пункт два формализации задачи звучит следующим образом. Состояние y_i на шаге i выражает суммарный вес предметов, решение о загрузке которых принято на шагах i, i+1,..., N при этом y₁=W y_i=0,1,...,W при i=2,3,...,N. В этой формулировке схему реализации называют «обратной прогонкой».

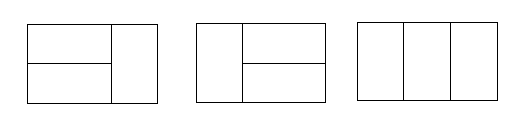
Комнату размером n*m единиц требуется покрыть одинаковыми плитками паркета размером 2*1 единиц без пропусков и наложений (m£20, n£8, m,n -целые). Пол можно покрыть паркетом различными способоми. Например, для m=2, n=3 все возможные способы укладки приведены на рисунке.

Требуется определить количество всех возможных способов укладки паркета для конкретных значений m£20, n£8. Результатом задачи является таблица, содержащая 20 строк и 8 столбцов.

Элементом таблицы является число, являющееся решением задачи для соответствующих n и m. На месте ненайденных результатов должен стоять символ «*».

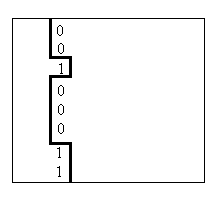
Решение. Пусть i - длина комнаты (1£i£8), j - ширина комнаты (1£j£20). «Разрежем» комнату на части. Разрез проводится по вертикали. Плитки, встречающиеся на пути разреза, обходим справа, т.е. при движении сверху вниз на каждом шаге либо обходим справа выступающую клетку, либо нет. При других укладках паркета могут получиться другие сечения. Все варианты сечений легко пронумеровываются, ибо это не что иное, как двоичное число: обход справа плитки соответствует 1, отсутствие обхода - 0. На рисунке сечение выделено «жирной» линией, ему соответствует двоичное число 00100011 (35). Количество различных сечений 2ⁱ (пронумеруем их от 0 до 2ⁱ-1), где i -длина комнаты.

Не будем пока учитывать то, что некоторые из сечений не могут быть получены. Обозначим парой (k,j) комнату с фиксированной длиной i, правый край которой не ровный, а представляет собой сечение с номером k. B[k,j] - количество вариантов укладки паркета в такой комнате. Задача в такой постановке сводится к нахождению B[0,j] - количество укладок паркета в комнате размером (i,j) с ровным правым краем.

Считаем, что B[0,0]=1 при любом i, ибо комната нулевой ширины, нулевого сечения и любой длины укладывается паркетом, при этом не используется ни одной плитки. Кроме этого считаем B[k,0]=0 для всех сечений с номерами k<>0, так как ненулевые сечения при нулевой ширине нельзя реализовать.

Попытаемся найти B[k,j] для фиксированного i. Предположим, что нам известны значения B[l,j-1] для всех сечений с номерами l (0£l£2ⁱ-1). Сечение l считаем совместимым с сечением k, если путем добавления целого числа плиток паркета из первого можно получить второе. Тогда B[k,j]=åB[l,j-1], суммирование ведется по всем сечениям l, совместимым с сечением k. Налицо динамическая схема решения задачи.

Оставляя пока в стороне вопрос совместимости сечений, «набросаем» логику решения.

Данные.

var B:array[0..255,0..20] of Comp;

A:array[1..8,1..20] of Comp;{Результирующая таблица}

function St2(k:integer):integer;{Вычисляем k - ю степень 2}

begin

if k<=0 then St2:=1 else St2:=2*St2(k-1);

end;

procedure Solve;{Основная логика}

var i,j,k,l,max:integer;

begin

for i:=1 to 8 do begin {Цикл по значению длины комнаты}

max:=St2(i)-1;

fillchar(B,sizeof(B),0);

B[0,0]:=1;

for j:=1 to 20 do begin {Цикл по значению ширины комнаты}

for k:=0 to max do {Сечение с номером k}

for l:=0 to max do{Сечение с номером l}

if Can(k,l,i) then B[k,j]:=B[k,j]+B[l,j-1];{Совместимость сечений «зарыта» в функции Can(k,l,i)}

A[i,j]:=B[0,j];

end;

end;

end;

Остался открытым вопрос о совместимости сечений. В этом случае необходимо различать понятия совместимость сечений в целом и совместимость в отдельном разряде. При анализе последнего входными данными являются значения разрядов сечений и информация о предыстории процесса (до текущего разряда) - целое или нецелое количество плиток уложено (значение переменной b). Выходными данными - признак - целое, нецелое количество плиток, требуемых для перевода сечения l в сечение k, или решение о том, что анализ продолжать не следует - сечения несовместимы. В данном случае этапу написания логики предшествует анализ на бумаге. Пример этой работы приведен в таблице.

Таблица

l	k	Значе-ние b	Новое значе- ние b или резуль- тат	Примечания
		false	false	До данного разряда уложено целое число плиток. Для перехода от l к k не надо ничего укладывать. Переходим к следующему разряду.
		true	несовмести-мы	До этого разряда уложено нецелое число плиток, а на этом «закрываем доступ». Сечения несовместимы.
		false	false	Укладываем целую плитку, количество уложенных плиток остается целым.
		true	несовмести-мы	Для перехода к новому сечению в этом разряде необходимо уложить целую плитку. Однако, укладывая её мы «перекрываем» доступ к нецелой плитке, уложенной до этого.
		false	true	До этого разряда между сечениями было уложено целое число плиток, а на этом можно уложить только полплитки.
		true	false	Нецелую плитку дополняем до целой.
		false	несовмести-мы	В этом разряде l лежит целая плитка. Необходимо уложить целую плитку для того, чтобы была 1 в этом разряде сечения k, но сделать этого мы не можем. Аналогично и для случая, когда b=true.

Данный анализ совместимости сечений реализован в функции Can.

function Can(k,l,pi:byte):boolean;{k,l -номера сечений, pi - количество анализируемых разрядов сечений}

var i,d:integer;b:boolean;

begin

Can:=false;b:=false;

for i:=1 to pi do begin

d:=St2(i);

if k and d =0 then{определяется значение разряда с номером d для сечения k}

if l and d =0 then b:=not(b)

else begin if b then exit end

else if (l and d<>0) or b then exit

end;

Can:=not(b);

end;

Осталось сделать еще несколько замечаний. Во-первых, если произведение n на m нечетно (размеры комнаты), то количество укладок паркетом такой комнаты равно 0. Во-вторых, при m=1 и четном n ответ равен 1. В-третьих, результирующая таблица симметрична относительно главной диагонали. В-четвертых, для комнат размером 2*t достаточно просто выводится следующая рекуррентная формула: A[2,t]=A[2,t-1]+A[2,t-2] (ряд Фибоначчи). Эти замечания реализуются на этапе предварительной обработки и приводят к незначительной модификации логики процедуры Solve. Еще одно замечание касается точности результата. Для больших значений n и m необходимо организовать вычисления с использованием длинной арифметики. Мы ограничимся маленькой хитростью - просто выпишем результат при выводе результирующей матрицы.

...

for i:=1 to 20 do begin

for j:=1 to 8 do

if (i=8) and (j=20) then write(‘3547073578562247994’:20)

else write(A[j,i]:20);

writeln;

end;

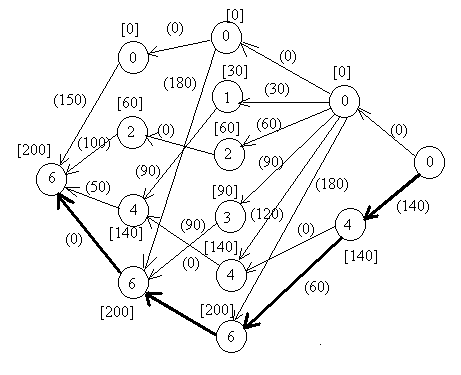
2.2.9. «Канадские авиалинии»

Вы победили в соревновании, организованном Канадскими авиалиниями. Приз - бесплатное путешествие по Канаде. Путешествие начинается с самого западного города, в который летают самолеты, проходит с запада на восток, пока не достигнет самого восточного города, в который летают самолеты. Затем путешествие продолжается обратно с востока на запад, пока не достигнет начального города. Ни один из городов нельзя посещать более одного раза за исключением начального города, который надо посетить ровно дважды (в начале и в конце путешествия). Вам также нельзя пользоваться авиалиниями других компаний или другими способами передвижения. Задача состоит в следующем: дан список городов и список прямых рейсов между парами городов; найти маршрут, включающий максимальное количество городов и удовлетворяющий вышеназванным условиям.

Сделаем первоначальное упрощение задачи. Пусть нам необходимо попасть из самого западного города в самый восточный, посетив при этом максимальное количество городов. Связи между городами будем записывать с помощью массива West:

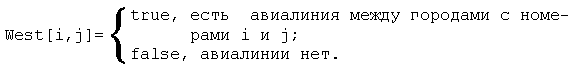
Пусть мы каким-то образом решили задачу для всех городов, которые находятся западнее города с номером i, т.е. для городов с номерами 1..(i-1). Что значит решили? У нас есть маршруты для каждого из этих городов, и нам известно, через сколько городов они проходят. Обозначим через множество городов западнее i и связанных с городом i авиалиниями. Для этих городов задача решена, т.е. известны значения d[j] (j ) - количество городов в наилучшем маршруте, заканчивающемся в городе с номером j.

Итак:

d[i]:=0;

for j Q_i do

if d[j]+1>d[i] then d[i]:=d[j]+1;

Остается открытым вопрос, а где же маршрут? Ибо значение d дает только количество городов, через которые он проходит. А для этого необходимо запомнить не только значение d[i], но и номер города j, дающего это значение. Возможно использование следующей структуры данных:

A:array[1..max] of record

d, l:byte;

end;

И реализация сказанного имеет вид:

FillChar(A,SizeOf(A),0);

A[1].d:=1;

for i:=2 to n do begin

for j:=1 to i-1 do if west[j,i] then if A[j].d+1>A[i].d then begin

A[i].d:=A[j].d+1;

A[i].l:=j;

end;

end;

Видим, что это не что иное, как метод динамического программирования в действии. Осталось выполнить обратный просмотр массива A по значениям поля l, начиная с элемента A[n].l и вывести из массива name:array[1..max] of string[15] названия городов.

Этот вывод можно осуществить с помощью следующей простой рекурсивной процедуры.

procedure rec(i:byte);

begin

if i<>1 then begin rec(A[i].l); writeln(name[i]);end;

end;

Как обобщить этот набросок решения для первоначальной формулировки задачи? Для удобства перенумеруем города в обратном порядке - с востока на запад. Изменим массив A:

A:array[1..max,1..max] of record

d,l:byte;

end;

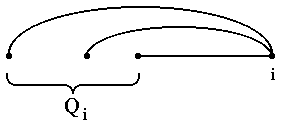
Под элементом A[i,j].d - путь из города i в город j - понимается максимальное число городов в маршруте, состоящем из двух частей: от i до 1 (на восток) и от 1 до j (на запад). По условию задачи нам необходимо найти наилучший по числу городов путь из n-го города в n-й. Считаем, что A[1,1].d=1 и A[i,j]=A[j,i]. Через Q_i обозначим множество городов, из которых можно попасть в город i. Верны следующие соотношения:

· A[i,j].d=max(A[k,j].d+1), при kÎQ_i, k<>j, если j<>1;

· A[i,i].d=max(A[k,i].d), при i>1 и kÎQ_i.

Рассмотрим логику формирования элементов массива A на следующем примере.

Основываясь на вышеприведенных соотношениях, выполним трассировку (ручную прокрутку задачи). Результаты приведены в таблице. Прочерк в клетке означает, что действия (вычисления) не выполнялись, знак «~» - сравнение. Присвоение симметричным относительно главной диагонали A элементам происходит одновременно (в таблице не приведены).

i	j	Qi	k	Действия
		[1]		A[2,1].d:=A[1,1].d+1=2 A[2,1].l:=1
		-	-	-
		[1]		A[3,1].d:=A[1,1].d+1=2 A[3,1].l:=1
		[1]		A[3,2].d:=A[1,2].d+1=3 A[3,2].l:=1
		-	-	-
		[3]		A[4,1].d:=A[3,1].d+1=3 A[4,1].l:=3
		[3]		A[4,2].d:=A[3,2].d+1=4 A[4,2].l:=3
		[3]		-
		-	-	-
		[2,3,4]		A[5,1].d:=A[2,1].d+1=3 A[5,1].l:=1
		[2,3,4]		A[5,1].d~A[3,1].d+1
		[2,3,4]		A[5,1].d:=A[4,1].d+1=4 A[5,1].l:=4
		[2,3,4]		-
		[2,3,4]		A[5,2].d:=A[3,2].d+1=4 A[5,2].l:=3
		[2,3,4]		A[5,2].d:=A[4,2].d+1=5 A[5,2].l:=4
		[2,3,4]		A[5,3].d:=A[2,3].d+1=4 A[5,3].l:=2
		[2,3,4]		-
		[2,3,4]		A[5,3].d~A[4,3].d+1
		[2,3,4]		A[5,4].d:=A[2,4].d+1=5 A[5,4].l:=2
		[2,3,4]		A[5,4].d~A[3,4].d+1
		[2,3,4]		-
		[2,3,4]		A[5,5].d:=A[2,5].d+1=6 A[5,5].l:=2
		[2,3,4]		A[5,5].d~A[3,5].d+1
		[2,3,4]		A[5,5].d~A[4,5].d+1

После этой прокрутки массив A по полю d имеет вид:

A[i,j].d

а по полю l («*» обозначено неопределенное значение):

A[i,j].l
	*
				*
			*

Попробуем по этой таблице вывести путь для нашего примера с помощью следующей процедуры:

procedure Way(i,j:integer);

begin

if (i=1) and (j=1) then writeln(name[1])

else if i>=j then begin

writeln(name[i]);

Way(A[i,j].l,j);

end

else begin

Way(i,A[i,j].l);

writeln(name[j]);

end;

end;

Получаем цепочку: Way[5,5] ® Way[2,5] ® Way[2,4] ® Way[2,3] ® Way[2,1] ®Way[1,1]. Жирным шрифтом выделены процедуры, в которых имя города выводится на входе в рекурсию, курсивом - на выходе из рекурсии. Цепочка имеет вид: 5 2 1 3 4 5 (индексы городов, напомним, что нумерация изменена для удобства на противоположную).

Осталось привести процедуру нахождения A (ее фрагмент).

...

FillChar(A,SizeOf(A),0);

A[1,1].d:=1;

for i:=2 to n do

for j:=1 to i do

if (i<>j) or (i=n) then

for kÎQ_i do

if ((k<>j) or (j=1)) and (A[k,j].d<>0) and (A[k,j].d+1>A[i,j].d) then

begin

A[i,j].d+A[k,j].d+1;A[j,i].d:=A[i,j].d;

A[i,j].l:=k;A[j,i].l:=A[i,j].l;

end;

Рассмотрим решения задачи методом полного перебора вариантов. Для этого требуется ряд дополнительных структур данных, а именно:

New:array[1..max] of boolean;

way_r:array[1..2*max] of byte;

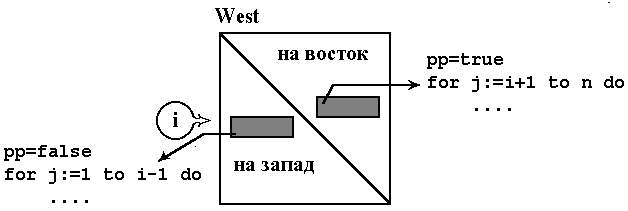
Первый массив необходим для хранения признака - посещался или нет город (New[i]=true - города с номером i нет в маршруте). Во втором и третьем массивах запоминаются по принципу стека текущий и наилучший маршруты соответственно. Для работы со стеками необходимы указатели - переменные yk и yk_max. Логика перебора поясняется на нижеприведенном рисунке. Ищем путь из города с номером i.

Фрагмент основной программы.

begin

...

FillChar(New,SizeOf(New),true);

yk:=1;Way[yk]:=1;pp:=true;yk_max:=0;

rec(1);

...

(* Вывод результата *)

...

end.

И процедура поиска решения.

procedure rec(i:byte);

var j,pn,pv:byte;

begin

if i=n then pp:=false; (* меняем направление *)

if (i=1) and not pp then begin

(* вернулись в первый город *)

if yk>yk_max then begin (* запоминаем решение *) yk_max:=yk;

way_r:=way;

end;

pp:=true; (* продолжаем перебор *)

end;

(* по направлению определяем номера просматриваемых городов*)

if pp then begin pn:=i+1; pv:=n end

else begin pn:=1; pv:=i-1 end;

for j:=pn to pv do begin if West[i,j] and New[j] then begin

(* в город с номером j летают самолеты из города i и город j еще не посещался *)

(* включаем город j в маршрут *)

Inc(yk);Way[yk]:=j;New[j]:=false;

rec(j);

(* исключаем город j из маршрута *)

New[j]:=true;Way[yk]:=0;Dec(yk);

(* если исключается самый восточный город (n), то меняем направление *)

if j=n then pp:=true;

end;

end;

Следует отметить, что при этой реализации упрощается вывод результата.

writeln(n);

writeln(yk_max-1);

for i:=1 to yk_max do writeln(name(Way_r[i]]);

Целесообразно сравнение решений при больших значениях n по времени выполнения.

2.3. Метод «решета»

Идея метода. Решето представляет собой метод комбинаторного программирования, который рассматривает конечное множество и исключает все элементы этого множества, не представляющие интереса. Он является логическим дополнением к процессу поиска с возвратом (backtrack), который перечисляет все элементы множества решений, представляющие интерес.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Числа, выделенные «жирным» шрифтом, отбрасываются. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Числа, выделенные курсивом, отбрасываются.

Эратосфен - греческий математик, 275-194 гг. до нашей эры. Классическая задача поиска простых чисел в интервале [2..N] - инструмент для обсуждения метода. Объяснение строится на основе следующего рисунка и фрагмента логики.

Const N=...;{верхняя граница интервала чисел}

Type Number=Set of 2..N;{решето, N<256}

Var S:Number;

procedure Poisk(var S:Number);

var i,j:2..N;

begin

S:=[2..N];

for i:=2 to N div 2 do

if i in S then begin

j:=i+i;

while j<=N do begin S:=S-[j];j:=j+i;end;

end;

end;

Логическим развитием задачи является ее решение при N больших 256. В этом случае необходимо ввести массив с множественным типом данных элементов.

Дата добавления: 2014-11-28