Энергия связи ядра

Энергия, которую необходимо затратить, чтобы разделить ядро на свободные нуклоны, не сообщая им кинетической энергии, называется полной энергией связи ядра (∆Е [Дж, МэВ]).

Так как энергия свободных нуклонов больше, чем энергия ядра как целого, полную энергию связи можно выразить

∆E = E_сум – E_я ,

где Е_сум – суммарная собственная энергия свободных нуклонов, на кото­рые можно разделить ядро;

Е_я – собственная энергия ядра как целого.

По соотношению Эйнштейна собственная энергия выражается

Е_я = т_я ∙ с²

Определим суммарную собственную энергию нуклонов

E_сум = (M_p + M_n ) ∙c² = (Z ∙ m_p + (A – Z) ∙ m_n) · c²,

где m_я – масса ядра, кг;

Z – зарядовое число;

М_р и М_n – суммарные массы всех протонов и нейтронов;

А – массовое число;

m_p и m_n – массы протонов и нейтронов.

Полная энергия связи ядра через массу выражается следующим образом:

∆E = (Z ∙ m_p + (A – Z) ∙ m_n – m_я) ∙ c²,

где m – масса, кг;

∆Е – полная энергия связи ядра, Дж.

Экспериментально определяют не массу ядра, а массу атома и через нее выражают энергию связи:

М_ат = т_я+ М_е = т_я + Z ∙ т_e,

где М_ат – масса атома;

М_e – масса электронной оболочки;

m_е – масса одного электрона.

Выражаем массу ядра

т_я = М_ат–Z ∙ т_е.

Определяем полную энергию связи атома через массу:

∆E = (Z ∙ m_p + (A – Z) ∙ m_n – M_ат + Z ∙ m_e ) ∙ c² =

= (Z (т_е + т_р ) + (A – Z) ∙ т_n – М_ат ) ∙ с² =

= (Z∙ 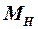+ (A – Z) ∙ m_n – M_am) ∙ c²,

где m_e + m_p = M_H – атом водорода.

При объединении свободных нуклонов в ядро должна выделяться энергия, равная полной энергии связи этого ядра. Поэтому энергетический эффект любой ядерной реакции рассчитывается как разность между сум­марной полной энергией связи продуктов и суммарной полной энергией компонентов.

ΔЕ – это энергия, которую необходимо затратить, чтобы разделить ядро на нуклоны, не сообщая им кинетической энергии. Это та энергия, которая должна выделиться при объединении свободных нуклонов в ядро. Для упрощения проведения расчётов энергетического эффекта реакций, вместо полной энергии связи ΔЕ, часто используется дефект масс

,

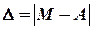где Δ – дефект масс;

М – масса ядра;

А – массовое число.

Дефект массы не имеет физического смысла. Косвенно характеризует величину ΔЕ, но значительно упрощает проведение расчётов. ΔЕ характеризует устойчивость ядра, но не позволяет сравнить относительную устойчивость различных ядер. Для этой цели используется удельная энергия связи.

Удельная энергия связи. Удельная энергия связи характеризует среднюю энергию связи одного нуклона с ядром. Это такая энергия, которую необходимо затратить, чтобы вырвать из ядра один нуклон, не передавая ему кинетической энергии, что следует из выражения

,

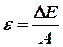где 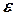- удельная энергия связи;

А – массовое число, которое показывает количество нуклонов в ядре.

Чтобы сравнить устойчивость различных ядер, изучается зависимость удельной энергии связи от массового числа и по данным таблицы 1.1 построен рисунок 1.1.

Таблица 1.1.

А
ε, МэВ	2,29	7,9	8,5	8,5	8,0	7,4

Рис. 1.1. Зависимость удельной энергии связи от массового числа

Зависимость начинается с точки с массовым числом 2. Если в ядре меньше 2-х нуклонов, понятие удельной энергии связи теряет физический смысл. Из такого ядра нельзя вырвать один нуклон, не разрушив само ядро.

Изгибы кривой показывают, что наиболее легкие ядра имеют аномально низкие, относительно средних, значения удельной энергии связи ε и, следовательно, устойчивость. Наибольшей устойчивостью обладают ядра средней массы с массовыми числами от 50 до 60. Затем устойчивость плавно снижается до урана (²³⁸U) и остаётся практически неизменной для более тяжёлых ядер. Данная зависимость справедлива для устойчивых изотопов, которые обычно указываются в периодической системе Менделеева (ПСМ). На рис. 1.1 можно выделить два участка (1, 2), на каждом из которых происходит увеличение удельной энергии связи, следовательно, каждый из них будет соответствовать процессу, в котором выделяется энергия.

Участок 1 соответствует термоядерному синтезу. В этом процессе из 2-х наиболее лёгких ядер образуется более тяжёлое, у которого при незначительном увеличении массы резко возрастает удельная энергия связи. За счёт этого увеличения выделяется огромное количество энергии (до 5 МэВ на 1 нуклон). Процессы термоядерного синтеза являются источником энергии звёзд и лежат в основе водородной бомбы. Это наиболее мощный из известных источников энергии, но он в настоящее время является неуправляемым.

Наиболее мощный управляемый источник энергии – деление тяжёлых ядер. Этому процессу соответствует участок 2 на рис. 1.1. Удельная энергия связи продуктов ≈ на 1 МэВ больше, чем исходных составляющих. Поэтому в этом процессе может выделиться до 1 МэВ на 1 нуклон. Деление тяжёлых ядер является источником энергии всех действующих ядерных реакторов и лежит в основе атомной бомбы. Более тщательное изучение рассмотренной выше закономерности позволило получить ряд выводов, которые легли в основу теории ядерных сил. При более глубоком рассмотрении кривая зависимости состоит из небольших максимумов и минимумов. Максимумы устойчивости располагаются на кривой строго в определённом порядке в соответствии со следующими закономерностями:

– наибольшие максимумы устойчивости наблюдаются для «чётно-чётных» ядер, т.е. ядер, у которых чётное число протонов и чётное число нейтронов. Это указывает на то, что внутри ядра нуклоны объединяются в группы и наибольшей устойчивостью обладает группа 2n2p. Устойчивость данной группы позволяет объяснить возможность α-распада, при котором из ядра вылетает ядро гелия (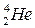), состоящее из 2-х протонов и 2-х нейтронов;

– менее интенсивные максимумы устойчивости наблюдаются для ядер, у которых число протонов и (или) число нейтронов соответствует следующим числам: 2, 8, 20, 28, 82, 126. Эти числа называют «магическими» ядерными числами. Наличие максимумов устойчивости при строго определённых числах протонов и (или) нейтронов указывает на то, что нуклоны внутри ядра образуют оболочки, аналогичные электронным оболочкам в атоме, и наибольшая устойчивость наблюдается при полностью заполненных оболочках;

– лёгкие ядра более устойчивы, когда число нейтронов равно числу протонов. Тяжёлые ядра более устойчивы, когда число нейтронов больше, чем число протонов;

– при сравнении устойчивости нескольких ядер наиболее устойчивы будут те ядра, для которых справедливы сразу несколько из выше перечисленных закономерностей.

Все закономерности справедливы для устойчивых ядер, которые обычно указаны в ПСМ. Если изотоп имеет меньшее массовое число, чем указано в ПСМ, то велика вероятность того, что он будет β⁺-активным, т.е. протон внутри такого ядра будет стремиться превратиться в нейтрон. Если масса изотопа больше, чем указано в ПСМ, то возрастает вероятность того, что он будет β^--активным, т.е. в таком ядре нейтрон будет стремиться превратиться в протон. В обоих случаях ядро становится неустойчивым, и его распад ведёт к восстановлению соотношения протонов и нейтронов.

Используя график и основные вышеизложенные закономерности, сравнивается устойчивость различных ядер. На примере химических элементов азота, кислорода и углерода определим устойчивость этих элементов:

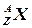
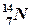
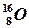
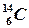
Устойчивость

Находим все указанные в условии задачи ядра в ПСМ по их зарядовым числам. Если указанная там относительная атомная масса какого-либо элемента отличается от данного в условии массового числа, значит, указанный в условии изотоп радиоактивный и наименее устойчивый.

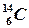– относительная атомная масса этого элемента отличается от указанного в ПСМ, и, следовательно, этот элемент наименее устойчив, склонен к радиоактивному распаду.

Определяем положение оставшихся ядер на графике зависимости удельной энергии связи от массового числа (рис. 1). Наиболее устойчивы ядра с массовым числом от 50 до 60. Если массовые числа меньше 50 или больше 60, а также в случае, когда все предложенные ядра имеют массовые числа от 50 до 60, к ним применяют критерии устойчивости. Количество протонов определяется по порядковому номеру элемента в периодической системе Д.И.Менделеева, а количество нейтронов определяется по разности между массовым числом, указанным в условии задачи, и количеством протонов. Если для двух ядер выполняются одинаковые критерии устойчивости, то их сравнивают между собой по положению на рис. 1.1 зависимости удельной энергии связи от массового числа.

Величина удельной энергии связи так же, как и величина полной энергии связи, используется для расчётов энергетического эффекта реакции. С целью упрощения таких расчётов вместо ε используют упаковочный коэффициент 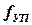, который определяется из выражения

.

Он представляет собой средний дефект массы, приходящийся на 1 нуклон ядра. Упаковочный коэффициент f_УП так же, как и дефект массы, не имеет физического смысла и лишь косвенно характеризует удельную энергию связи ε, а также существенно упрощает проведение расчётов.

Дата добавления: 2014-11-29