Индексы среднего уровня

Факторный анализ индексных моделей

Связь между изменениями объема товарооборота, количеством продажи товаров и уровнем их цен выражается в системе взаимосвязанных индексов товарооборота. Индекс товарооборота в фактических ценах вычисляется по следующей формуле:

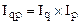
На основе этой формулы выявляется влияние отдельных факторов на изменение товарооборота. Зная изменение товарооборота I_qp и цен I_p можно определить изменение товарооборота в неизменных (сопоставимых) ценах:

.

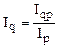По известным индексам товарооборота в фактических ценах I_qp и товарооборота в сопоставимых ценах I_q определяется индекс цен

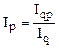
Качественные индексируемые показатели часто отображаются средними величинами (средняя цена по области, и т.д.). Общая средняя величина качественного показателя – это взвешенная средняя из частных средних которая зависит от уровня цен на отдельные товары и от удельного веса каждого товара в общем его вкладе в формировании цены. При анализе динамики среднего уровня возникает вопрос в какой мере изменение среднего уровня обусловлено действием каждого фактора в отдельности.

Индексы, отражающие изменение средних уровней за счет двух факторов: изменения данных уровней и изменения удельных весов (структуры) совокупности, называются индексами среднего уровня, или индексами переменного состава. Он состоит из двух сомножителей. Первый показывает, как изменяется средний уровень под влиянием изменения качественного показателя – индекс фиксированного состава. Второй показывает влияние изменения структуры и называется индексом структурных сдвигов.

Индекс переменного состава: ,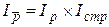

Где, 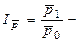индекс средних цен (переменного состава);

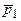и 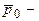средние взвешенные цены по количеству реализованных товаров: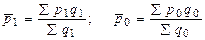

Влияние структуры реализации товаров на среднюю цену показывает индекс структурных сдвигов:

,

Где, расчетная средняя цена текущего периода; средняя цена базисного периода.

В абсолютном выражении это абсолютный прирост средней цены (переплата) за каждый килограмм:

.

Влияние изменения отдельных цен на среднюю величину цены показывает индекс фиксированного состава:

.

Пример 1. Известно количество продаж и цены в магазинах.

Определить:

1. индексы переменного состава, постоянного состава и структурных сдвигов;

2. величины абсолютных приростов за счет действия каждого фактора.

Магазин	Базисный период	Текущий Период	Индивидуальный индекс цен, ip
Цена за 1 ед., руб. р0	Объем, шт. q0	Цена за 1 ед., руб. p1	Объем, шт. q1
					0,96
					0,97
					0,95
Итого:	-		-		-

Решение: Определим средние цены в отчетном и базисном периодах:

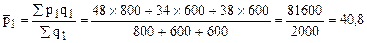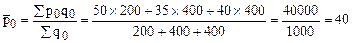руб.

руб.

Индекс средних цен или переменного состава:

.

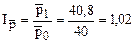Средняя цена реализации возросла на 2%. Прирост средней цены реализации: 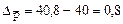руб.

Население при покупке каждого килограмма продукта переплачивало по 0,8 руб.

Индекс структурных сдвигов:

.

Структурные сдвиги (изменение долей продаж) в реализации объема продукции вызвали повышение средней цены на 6,25%.

руб.

Переплата населением на каждый килограмм продукции составила 2,5 руб.

Индекс постоянного состава:

Индекс показывает снижение цены на 3,8%. За счет снижения цен произошла экономия в общей сумме

руб.

Экономия на каждый килограмм составила руб.

Рассчитаем индекс средних цен другим способом (мультипликативная модель):

Величина изменения средней цены продаж составила:

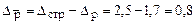руб.

Пример 2. Имеются данные о реализации товара. Определить индивидуальные и общие индексы; абсолютный прирост за счет действия отдельных факторов.

Товар	Базисный период	Текущий Период	Индивидуальный индекс
Цена за 1 ед., руб. р0	Объем, шт. q0	Цена за 1 ед., руб. p1	Объем, шт. q1	цен, ip	объема, i q
А, т					1,25	1,27
Б, м					1,0	1,25
В, шт.					0,67	1,5

Решение: Результаты расчета индивидуальных индексов цен и физического объема находятся в таблице.

Общий индекс цен:

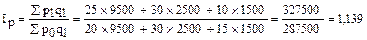или 113,9%

По данному ассортименту товаров в целом цены повысились на 13,9%.

Абсолютный прирост товарооборота за счет изменения цен:

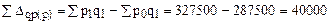руб.

Повышение цен на 13,9% обусловило увеличение объема товарооборота в текущем периоде на 40 тыс. руб., что привело к перерасходу денежных средств населением на 40 тыс. руб.

Общий индекс физического объема:

или 127,8%.

Прирост физического объема реализации в текущем периоде составил в среднем 27,8%.

Сумма прироста товарооборота за счет изменения объема продаж:

руб.

В результате изменения физического объема реализации товаров в текущем периоде получен прирост объема товарооборота в сопоставимых ценах на 62,5 тыс. руб.

Общий индекс товарооборота в текущих ценах вырос на 45,5%.

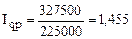или 145,5%

Прирост товарооборота в текущем периоде по сравнению с базисным:

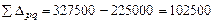руб.

Пример 3. в таблице представлены данные о продаже товаров в магазине. Определить: общий индекс цен; общий индекс физического объема; прирост товарооборота за счет изменения цен; прирост товарооборота за счет изменения объема продаж.

Товар	Продажа в ценах соответствующего периода	Изменение цен в текущем	Расчет
	базовый период q0p0	текущий период q1p1	периоде по сравнению с базовым, %
А	153,5	185,0	-4	0,96	192,71
Б	245,0	260,6	+10	1,1	236,91
В	21,5	29,4	без измен.	1,0	29,4
Итого	420,0	475,0	–	–	459,02

Решение: Индивидуальные (однотоварные) индексы цен:

По каждому товару определим стоимость продажи товара в текущем периоде по ценам базисного:

Общий индекс цен:

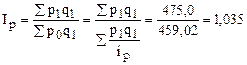или 103,5%,

Т.е. по данному ассортименту цены повышены на 3,5%.

Прирост товарооборота за счет изменения цен:

тыс. руб.

Определим общий индекс физического объема товарооборота в сопоставимых (базисных) ценах:

или 109,3%,

Т.е. физический объем продажи товаров увеличился в текущем периоде на 9,3%.

Прирост товарооборота за счет изменения физического объема продажи товаров:

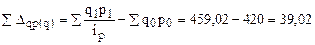тыс. руб.

Общий прирост товарооборота в текущем периоде:

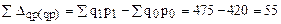тыс. руб.

Пример 4. Имеются данные о средней заработной плате работников и число работников организаций по трем отраслям.

№ п/п	Отрасль экономики	Заработная плата, руб.	Число работников, чел.
		Х0	Х1	Т0	Т1
	Здравоохранение Образование Культура и искусство

Определить индекс заработной платы переменного состава, постоянного состава и структурных сдвигов.

Решение: 1. Определим среднюю заработную плату работников в базисном периоде:

руб.

В отчетном периоде:

руб.

2. Индекс заработной платы переменного состава:

или 113,8%

Заработная плата выросла на 13,8%. Абсолютный прирост составил: 637,2 – 560 = 77,2 руб.

Изменение средней заработной платы происходило под влиянием двух факторов: уровня заработной платы и числа работников.

3. Индекс заработной платы постоянного состава:

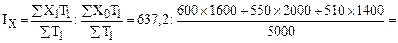
или 114,9%

Средняя заработная плата работников увеличилась на 14,9% за счет увеличения заработной платы. Абсолютный прирост средней заработной платы составил: 637,2 – 554,8 = 82,4 руб.

4. Индекс структурных сдвигов:

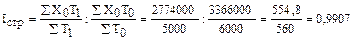или 99,07%

Увеличение доли работников с низкой заработной платой в общей численности привело к снижению средней заработной платы на 0,03%. Абсолютное снижение составило: 554,8 – 560 = –5,2 руб.

Пример 5. Имеются данные о продаже товаров в магазине:

Товар	Продано в отчетном периоде p1q1, тыс. руб.	Изменение цен на товары, %	Индивидуал. индексы цен, ip
Туфли муж., пар.		+3	1,03
Костюмы, шт.		+6	1,06
Итого:		–	–

Дата добавления: 2014-11-29