Проверка адекватности регрессионной модели

Параметрические методы изучения связи

Корреляционно-регрессионный анализ позволяет выбрать вид модели, оценить ее параметры, измерить тесноту связи, определить наиболее влияющие факторы на результативный признак.

Линейная форма связи и оценка ее параметров. При линейной форме связи зависимость результативного признака у от факторного показателя х определяется уравнением регрессии:

у_х = а₀ + а₁х.

Оценивание неизвестных параметров (а₀, а₁) производится методом наименьших квадратов (МНК) по исходным данным (y_i, x_i, i=1,2,…n). МНК дает систему нормальных уравнений:

,

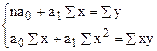решая которые находятся неизвестные параметры:

.

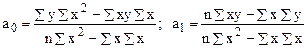Подставляя в общее уравнение найденные параметры, получим уравнение регрессии: .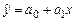

Введем обозначения:

Среднеквадратическое отклонение результативного признака yi от выровненных .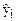
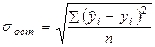
Среднеквадратическое отклонение факторного признака хi от средней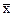
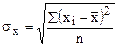
Общая дисперсия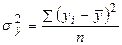
Среднеквадратическое отклонение модельных значений от средней.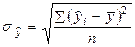
Межгрупповая дисперсия измеряет вариацию групповых средних вокруг общей средней. Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.

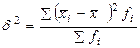
Для проверки з начимости коэффициентов линейной регрессии у_х = а₀ + а₁х при n<30 используют t-критерий Стьюдента. Для этого вычисляют расчетные значения t – критерия.

для параметра а₀: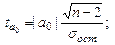

для параметра а₁: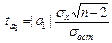

Полученные значения 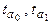сравнивают с критическими t_кр, которые определяют по таблице Стьюдента при заданном уровне значимости a (обычно a=0.05) и числом степеней свободы n=n-m=n-2. Параметр признается значимым, если t_расч > t_кр.

Теснота корреляционной связи между x и y может быть измерена империческим корреляционным отношением:

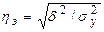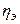(0≤ ≤1).

Чем ближе оно к 1, тем теснее связь. При 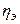=0 связи нет.

Теснота корреляционной связи между x и y при заданной зависимости определяется индексом корреляции:

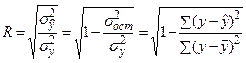(0≤R≤1).

Чем ближе R к 1, тем теснее связь. При R=0 связи нет. Величину R² называют коэффициентом детерминации. Коэффициент детерминации характеризует какая часть общей вариации у объясняется изучаемым фактором х.

Показателем тесноты линейной связи является линейный коэффициент корреляции:

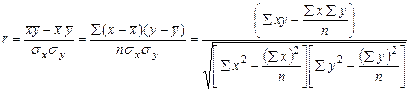(-1≤r≤1).

Величину r² называют линейным коэффициентом детерминации. Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента. Для этого вычисляют расчетные значения t – критерия

,

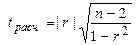где n-2 – число степеней свободы при заданном уровне значимости a (обычно a=0.05). Расчетное значение 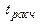сравнивают с табличными значениями t-критерия t_кр, которые определяют по таблице Стьюдента при заданном уровне значимости a (обычно a=0.05) и числом степеней свободы n=n-m=n-2. Параметр r признается значимым, если t_расч > t_кр.

Дата добавления: 2014-11-29