Тема 4. Принятие оптимального решения в условиях экономического риска

Риск − категория вероятностная, поэтому в процессе оценки неопределенности и количественного определения риска используют вероятностные расчеты.

Вероятностные задачи характеризуются тем, что эффективность принимаемых решений зависит не только от детерминированных факторов, но и от вероятностей их появления, т.е. известен закон распределения управляемых факторов X в виде:

			….
			….

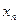
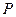
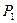
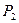
где 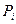есть вероятность появления управляемого фактора , .

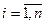Каждой паре соответствует значение функции эффективности 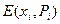. В качестве показателей эффективности могут выступать математическое ожидание , дисперсия , среднее квадратическое отклонение и другие вероятностные характеристики.

, , .

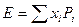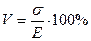Средняя величина E представляет собой обобщенную количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала.

Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.

Дисперсия не дает полной картины линейных уклонений 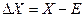, более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичными отклонениями с помощью известного неравенства Чебышева.

Вероятность Р того, что случайная величина Х отклоняется от своего математического ожидания больше, чем на заданный допуск 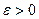, не превосходит ее дисперсии, деленной на , т.е.

.

Отсюда видно, что незначительному риску по среднеквадратическому отклонению соответствует малый риск и по линейным отклонениям: точки Х с большой вероятностью будут располагаться внутри -окрестности ожидаемого значения Е.

Все более признанным становится оценка рискованности посредством среднего квадратического отклонения .

Итак, будем считать, что риском операции называется число - среднее квадратическое отклонение управляемого фактора (например, дохода) Х операции, которое обозначим .

Если, например, под Х понимать случайный доход , то представляет собой средний ожидаемый доход, или эффективность, а среднее квадратическое отклонение является оценкой рискованности, риском и обозначается .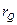

Коэффициент вариации V – безразмерная величина. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% –слабая колеблемость, 10-25% – умеренная колеблемость, свыше 25% – высокая колеблемость.

С помощью этого метода оценки риска, т.е. на основе расчета дисперсии, стандартного отклонения и коэффициента вариации можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом (проанализировав динамику ее доходов) за некоторый промежуток времени.

Преимуществом данного метода оценки предпринимательского риска является несложность математических расчетов, а явным недостатком – необходимость большого числа исходных данных (чем больше массив, те достовернее оценка риска)

Рассмотрим данный метод на конкретном примере. Сравним по риску вложения в акции трех типов А, В, С, если каждая из них по своему откликается на возможные рыночные ситуации, достигая с известными вероятностями определенных значений доходности.

Тип акций	Ситуация 1	Ситуация 2
вероятность	доходность	вероятность	доходность
А	0,5	20%	0,5	10%
В	0,99	15,1%	0,01	5,1%
С	0,7	13%	0,3	7%

По формулам находим для акции А:

,

,

, ;

для акции В:

,

,

, ;

для акции С:

,

,

, .

Так как наименьшее значение коэффициента вариации имеем для акции В, то и вложения в эту акцию наиболее предпочтительны, тем более, что и наименьшее.

Если имеются две стратегии A и B, для которых известны , , и 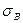, то предпочтение должно быть отдано стратегии A, если:

1. , 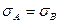и ,

2. , и ,

3. , и .

Рассмотрим другой метод исследования, основанный на предположении о том, что большинство результатов хозяйственной деятельности (прибыль, доход и т.д.) как случайные величины подчиняются закону, близкому к нормальному. Этот закон характерен для распределения событий в случае, когда их исход представляет собой результат совместного воздействия большого количества независимых факторов, и ни один из этих факторов не оказывает преобладающего влияния.

Нормальное распределение является основным элементом большинства систем управления риском. На нем целиком основан страховой бизнес, потому что от пожара в Москве не загораются дома в Самаре, а смерть определенного человека в одном месте, как правило, не имеет отношения к смерти другого человека в другом месте и в другое время. Когда страховые компании собирают сведения о миллионах людей обоего пола всех возрастов, значения ожидаемой продолжительности жизни оказываются распределенными по нормальной кривой. В силу этого страховые компании способны с большой степенью надежности оценивать продолжительность жизни разных групп населения. Они могут не только определить ожидаемую среднюю продолжительность жизни, но и диапазоны, в которых она может колебаться из года в год. Уточняя эти оценки на основе дополнительных данных, таких, как истории болезней, число курильщиков, постоянные места проживания, профессиональную деятельность, эти компании повышают точность оценки ожидаемой продолжительности жизни.

Порой нормальное распределение дает гораздо больше важной информации, чем простые оценки представительности выборки. Нормальное распределение менее вероятно, хоты и не исключено, когда наблюдения зависимы друг от друга, то есть когда вероятность события определяются предыдущим событием. Например, если у лучника проблемы со зрением, стрелы будут слева от яблочка, т.е. центр распределения будет сдвинут. В подобных ситуациях распределение относительно среднего значения обычно оказывается ассиметричным.

В таких случаях мы можем воспользоваться рассуждением наоборот. Если независимость событий является необходимым условием нормального распределения, можно предположить, что данные, распределение которых представлено нормальной кривой, получены на основе независимых наблюдений. Теперь мы можем поставить несколько интересных вопросов.

Насколько точно изменения курса акций на бирже подчинены законам нормального распределения? Некоторые знатоки рынка утверждают, что курс подвержен случайным колебаниям, напоминающим пошатывающего пьяного, пытающегося ухватиться за фонарный столб. Они полагают, что у курса не больше памяти, чем у рулетки или пары костей, и что каждое наблюдение независимо от предыдущего наблюдения. Сегодняшнее движение цен не зависит от того, что произошло минуту назад, вчера или позавчера.

Лучший способ решения вопроса о том, являются ли изменения курса акций независимыми событиями, заключается в сравнении колебаний курса с нормальным распределением. У нас есть веские основания утверждать, что эти колебания подчиняются нормальному закону, и в этом нет ничего удивительного. В условиях постоянной изменчивости и конкурентной борьбы на нашем рынке капитала, когда каждый инвестор стремится переиграть других, новая информация мгновенно отражается на котировках. Когда выясняется падение прибыли у General Motors или Merck объявляет о выпуске нового чудодейственного лекарства, котировки не стоят на месте в ожидании, пока инвесторы переварят информацию. Ни один инвестор не станет ждать, пока начнут действовать другие. На рынке действуют сворой, и новая информация немедленно изменит котировки акций General Motors или Merck. При этом сама новая информация поступает в случайном порядке. В силу этого изменения котировок непредсказуемы.

Нормальность распределения – это жесткая проверка гипотезы случайных колебаний рынка. Но нужна одна важная оговорка. Даже если гипотеза случайных колебаний адекватно описывает ситуацию на фондовом рынке, даже если изменения котировок описываются нормальным распределением, среднее значение изменений всегда отлично от нуля. Тенденция к повышению котировок не должна нас удивлять. Состояние владельцев акций со временем растет, как и сбережения, доходы и прибыли корпораций. Поскольку по большей части котировки не падают, а растут, среднее значение их изменений оказывается положительным.

На практике для проверки предположения о нормальном распределении исследуемой совокупности случайных факторов применяются различные критерии согласия, устанавливающие соответствие между эмпирическим (опытным) и теоретическим (нормальным) распределением, и которые для задаваемой надежности (вероятности) позволяют принять или отвергнуть принятую гипотезу о нормальном законе распределения.

Нормальное распределение (распределение Гаусса) представляет собой вид распределения случайных величин, с достаточной точностью описывающий распределение плотности вероятности результатов производственно- хозяйственной, финансовой, инновационной деятельности или изменений условий внешней среды, поскольку показатели, характеризующие их, определяются большим числом независимых случайных величин, каждая из которых в отдельности относительно других играет незначительную роль и непредсказуема. Применение нормального распределения для оценки рисков также связано с тем, что в основе данных, как правило, используется ряд дискретных значений. Эти теоретические предпосылки, а также апробация моделей для анализа рисков на основе нормального распределения доказывают адекватность этого теоретического инструмента реальным процессам экономической деятельности.

Плотность вероятности нормального распределения имеет вид:

где − математическое ожидание,

− среднее квадратическое отклонение случайной величины Х.

Из курса теории вероятностей известно, что попадание случайной величины Х в заданный интервал определяется как

,

где

есть интеграл вероятностей или функция Лапласа, ее значения в зависимости от параметра х приводятся в специальных таблицах, эта функция четная и она изменяется от 0 до 0,5.

В процессе принятия управленческих решений целесообразно различать и выделять определенные области (зоны риска) в зависимости от уровня возможных потерь. Для этого разработаны и используются так называемые шкалы риска. Ниже приведена эмпирическая шкала риска, которую рекомендуется применять.

Эмпирическая шкала допустимого уровня риска

№	Вероятность нежелательного исхода (величина риска)	Наименование градации риска
	0,0-0,1	Минимальный
	0,1-0,3	Малый
	0,3-0,4	Средний
	0,4-0,6	Высокий
	0,6-0,8	Максимальный
	0,8-1,0	Критический

Выбирая вероятности из таблицы «Эмпирическая шкала допустимого уровня риска» по таблицам функции Лапласа Ф(t) находим соответствующие значения параметра t.

P		0,1	0,3	0,4	0,5	0,6	0,8	0,9973
T		0,126	0,386	0,524	0,674	0,842	1,281

Наносим значения на график нормальной кривой влево и вправо от и строим зоны риска (не нарушая общности, значения откладываются только вправо) (рис. 4.1).

Рис. 4.1 Зоны риска для кривой нормального распределения вероятностей

Кривую представленную на рис. 4.1, можно называть кривой риска. На ней выделены следующие характерные точки и зоны.

Первая точка определяет вероятность нулевых потерь, ее можно считать максимальной, но, конечно, меньше единицы.

Вторая точка вероятности нежелательного исхода, соответствует «нормальному», «разумному» риску, при котором рекомендуется принимать обычные предпринимательские решения. Зона приемлемого (минимального) риска характеризуется уровнем потерь, не превышающим размера чистой прибыли.

Третья точка характеризуется величиной возможных потерь, равной ожидаемой прибыли, т.е. полной потерей прибыли. Зона допустимого (повышенного) риска характеризуется уровнем потерь, не превышающим размеры расчетной прибыли. Осторожные предприниматели стараются действовать так, чтобы возможная величина потерь не выходила за пределы допустимого риска.

Четвертая точка риска соответствует величине потерь, равных расчетной выручке. Зона критического риска характеризуется тем, что в границах этой зоны возможны потери расчетной прибыли, т.е. есть опасность потерять и средства, вложенные предпринимателем в операцию.

Пятая точка характеризуется потерями, равными имущественному состоянию предпринимателя. Зона катастрофического (недопустимого) риска характеризуется тем, что в границах этой зоны ожидаемые потери способны превзойти размер ожидаемых доходов от операций и достичь величины, равной всему имущественному состоянию предпринимателя (фирмы).

Вероятности определенных уровней потерь являются важными показателями, позволяющими высказывать суждение об ожидаемом риске и его приемлемости, поэтому построенную кривую и можно назвать кривой риска. Так, если вероятность катастрофической потери выражается показателем, свидетельствующим об ощутимой угрозе потери всего состояния, то осторожный предприниматель заведомо откажется от такого дела и не пойдет на подобный риск.

Если результаты экономической деятельности подчиняются нормальному закону распределения вероятностей, то в этом случае имеет место, так называемое, правило трех сигм, которое в более широкой постановке позволяет установить область возможных значений случайной величины X как

,

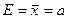где величина t характеризует доверительную вероятность попадания случайной величины X в интервал , а − среднее случайной величины X.

При с вероятность 0,6826 (или в 68% случаев) можно утверждать, что значение случайной величины лежит в пределах ; при с вероятностью 0,9544 можно утверждать, что 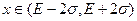; и при 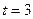вероятность того, что значение случайной величины 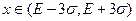, составляет 0,9973, то есть это событие практически достоверно.

Дата добавления: 2014-11-29