Статистическая проверка статистических гипотез

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Нулевой (основной) называют выдвинутую гипотезу Н₀.

Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой.

Различают гипотезы, которые содержат одно и более одного предположений.

Простой называют гипотезу, содержащую только одно предложение.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Статистическим критерием называют случайную величину К, которая служит для проверки гипотезы. Наблюдаемым (эмпирическим) значением К_набл называют то значение критерия, которое вычислено по выборкам.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью допустимых значений называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.

Критическими точками (границами) к_кр называют точки, отделяющие критическую область от области принятия гипотезы.

Правосторонней называют критическую область, определяемую неравенством К˃ к_кр, где к_кр - положительное число.

Левосторонней называют критическую область, определяемую неравенством К< к_кр, где к_кр - отрицательное число.

Двусторонней называют критическую область, определяемую неравенством К< к₁, К˃ к₂, где к₁ < к₂.

Сравнение двух дисперсий нормальных генеральных совокупностей.

По независимым выборкам, объемы которых n₁, n₂ извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии s_X² и s_Y². Требуется сравнить эти дисперсии.

Правило 1. Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу Н₀: D(X)=D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: D(X)˃D(Y), надо вычислить наблюдаемое значение критерия (отношение большой исправленной дисперсии к меньшей)

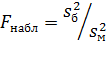
и по таблице критических точек распределения Фишера-Снедекора, по заданному уровню значимости α и числам степеней свободы

к₁ = n₁ -1, к₂ = n₂ -1 (к₁ - число степеней свободы большей исправленной дисперсии) найти критическую точку F_кр (α, к₁, к₂). Если 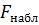< F_кр – нет оснований отвергнуть нулевую гипотезу, если 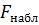˃ F_кр - отвергают нулевую гипотезу.

Правило 2. При конкурирующей гипотезе Н₁: D(X)≠D(Y) критическую точку F_кр (α/2, к₁, к₂) ищут по уровню значимости α/2 и числам степеней свободы к₁, к₂. Если 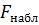< F_кр – нет оснований отвергнуть нулевую гипотезу, если 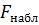˃ F_кр - отвергают нулевую гипотезу.

Пример. По двум независимым выборкам, объемы которых n₁ =11 и n₂=14, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии s_X² =0,76 и s_Y² =0,38. При уровне значимости α=0,05, проверить нулевую гипотезу Н₀: D(X)=D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе Н₁: D(X)˃D(Y).

Решение. Найдем отношение большой исправленной дисперсии к меньшей:

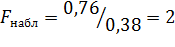
По условию конкурирующая гипотеза Н₁: D(X)˃D(Y), поэтому критическая область - правосторонняя.

По табл. приложения, по уровню значимости α=0,05 и числам степеней свободы к₁ = n₁ -1=11-1=10, к₂ = n₂ -1= 14-1=13 находим критическую точку

F_кр (0,05,10, 13)=2,67. Так как 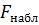< F_кр – нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий. Другими словами, выборочные исправленные дисперсии различаются незначимо.

Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности.

Обозначим через n объем выборки, по которой найдена исправленная дисперсия s².

Правило 1. Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу Н₀: σ²=σ₀² о равенстве неизвестной дисперсии σ² гипотетическому (предполагаемому) значению σ₀² при конкурирующей гипотезе Н₁: σ²˃σ₀², надо вычислить наблюдаемое значение критерия

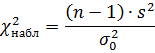
и по таблице критических точек распределения χ², по заданному уровню значимости α и числу степеней свободы к = n -1 критическую точку χ²_кр(α, к). Если 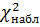< χ²_кр -нет оснований отвергнуть нулевую гипотезу,

если 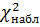˃ χ²_кр - отвергают нулевую гипотезу.

Пример. Из нормальной генеральной совокупности извлечена выборка объема n= 21, и по ней найдена исправленная выборочная дисперсия s²=16,2. Требуется при уровне значимости 0,01 проверить нулевую гипотезу Н₀: σ²=σ₀²=15, приняв в качестве конкурирующей гипотезы Н₁: σ₀²˃15.

Решение. Найдем наблюдаемое значение критерия:
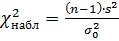=21,6

По условию конкурирующая гипотеза Н₁: σ₀²˃15, поэтому критическая область- правосторонняя. По таблице приложения, по уровню значимости 0,01 и числу степеней свободы к = n -1=21-1=20 находим критическую точку χ²_кр(0,01, 20)=37,6.

Так как 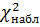< χ²_кр -нет оснований отвергнуть нулевую гипотезу о равенстве генеральной дисперсии σ² гипотетическому (предполагаемому) значению. Другими словами, различие между исправленной дисперсией и гипотетической незначимо.

Дата добавления: 2014-11-28