Задачи теории статистических решений

Близкой по идеям и методам к теории игр являет­ся теория статистических решений. От те­ории игр она отличается тем, что неопределенная си­туация не имеет конфликтной окраски — никто нико­му не противодействует, но элемент неопределенности налицо. В задачах теории статистических решений не­известные условия операции зависят не от сознатель­но действующего «противника» (или других участни­ков конфликта), а от объективной действительности, которую в теории статистических решений принято называть «природой». Соответствующие ситуации час­то называются «играми с природой». «Природа» мыс­лится как некая незаинтересованная инстанция, «поведение» ко­торой неизвестно, но, во всяком случае, не злонаме­ренно.

Рассмотрим игру с природой: у нас (сторона А) имеется т возможных стратегий А₁, А₂,..., А_т; об обстановке можно сделать n пред­положений: H₁, Н₂,..., Н_n. Расcмотрим их как «стра­тегии природы». Наш выигрыш a_ij при каждой паре стратегий A_i, H_j задан матрицей (таблица 9).

Таблица 9

	Н1	Н2	…	Нn
А1	a11	a12	…	a1n
А2	a12	a22	…	a2n
…	…	…	…	…
Аm	am1	am2	…	amn

Требуется выбрать такую стратегию игрока А (чис­тую или, может быть, смешанную, если это возможно), которая является более выгодной по сравнению с дру­гими.

С первого взгляда кажется, что эта задача похожа на игру двух игроков А и H с противоположными ин­тересами и должна решаться теми же методами. Но это не совсем так. Отсутствие противодействия со сто­роны природы делает ситуацию качественно другой.

Самый про­стой случай выбора решения в игре с природой — это случай когда какая-то из страте­гий игрока А превосходит другие («доминирует» над ними). В этом случае выигрыш при доминирующей стратегии при любом сос­тоянии природы не меньше, чем при других стратеги­ях, а при некоторых — больше.

Если даже в матрице игры с природой нет одной доминирующей над всеми другими, все же полезно посмотреть, нет ли в ней дублирующих стратегий и уступающих другим при всех условиях (как мы это делали, упрощая матрицу игры). Но здесь есть одна тонкость: так мы можем уменьшить только число стра­тегий игрока А, но не игрока Н - ему ведь все равно, много или мало мы выиграем! Предположим, что «чист­ка» матрицы произведена, и ни дублирующих, ни за­ведомо невыгодных игроку А стратегий в ней нет.

Чем же все-таки руководствоваться при выборе ре­шения? Вполне естественно, должна учитываться мат­рица выигрышей (а_ij). Однако в каком-то смысле кар­тина ситуации, которую дает матрица (а_ij), неполна и не отражает должным образом достоинств и недостат­ков каждого решения.

Поясним эту мысль. Предпо­ложим, что выигрыш а_ij при нашей стратегии A_i и со­стоянии природы H_j больше, чем при нашей стратегии A_k и состоянии природы H_d: а_ij > а_kd. Но за счет чего больше? За счет того, что мы удачно выбрали стра­тегию A_ij? Необязательно. Может быть, просто состоя­ние природы H_j выгоднее нам, чем H_d. Например, со­стояние природы «нормальные условия» для любой опе­рации выгоднее, чем «наводнение», «землетрясение» и т. п. Желательно ввести такие показатели, которые не просто давали бы выигрыш при данной стратегии в каждой ситуации, но отражали бы «удачность» пли «неудачность» выбора данной стратегии в данной ситуации.

С этой целью в теории решений вводится понятие «риска».

Риском r_ij игрока А при пользовании стра­тегией A_i в условиях H_j называется разность между выигрышем, который мы получили бы, если бы знали условия H_j и выигрышем, который мы получим, не зная их и выбирая стратегию A_i.

Очевидно, если бы мы (игрок А) знали состояние природы H_j, мы выбрали бы ту стратегию, при кото­рой наш выигрыш максимален. Этот выигрыш, макси­мальный в столбце H_j, мы уже раньше встречали и обозначили β_j. Чтобы получить риск r_ij, нужно из β_j вычесть фактический выигрыш а_ij

r_ij = β_j - а_ij.

Для примера возьмем матрицу выигрышей (а_ij) (таблица 10) и построим для нее матрицу рисков (r_ij) (таблица 11).

Таблица 10

	Н1	Н2	Н3	Н4
А1
А2
А3
βj

Таблица 11

	Н1	Н2	Н3	Н4
А1
А2
А3

При взгляде на матрицу рисков (таблица 28.4) нам становятся яснее некоторые черты данной «игры с природой». Так, в матрице выигрышей (а_ij)

(таблица 10) во второй строке первый и четвертый элементы равны друг другу. Однако эти вы­игрыши совсем не равноценны в смысле удачного вы­бора стратегии: r₂₁ = 1, r₂₄ = 6. Естественно, нам хотелось бы минимизировать риск, сопровождающий выбор решения.

Исходя из приведенных выше рассуждений возможны две постановки задачи о выбо­ре решения: при одной нам желательно получить мак­симальный выигрыш, при другой — минимальный риск.

Известно, что самый простой случай неопределен­ности - это «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют ка­кие-то вероятности Q₁, Q₂,..., Q_n и эти вероятности нам известны. В этом случае логичгл выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально

.

Необходимо отметить, что та же стратегия, кото­рая обращает и максимум средний выигрыш, обраща­ет в минимум и средний риск

,

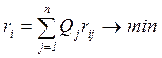так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно и то же оптимальное решение.

Допустим, что вероятности Q₁, Q₂,..., Q_n в принципе существуют, по нам неизвестны. Иногда в этом случае предполагают все состояния природы рав­новероятными (так называемый «принцип недостаточ­ного основания» Лапласа). В других случаях для того, чтобы найти ориентировочные значения ве­роятностей Q₁, Q₂,..., Q_n исполь­зуется метод экспертных оценок.

Дата добавления: 2014-11-29