Основные критерии статистических решений

Рассмотрим решение задачи в общем виде, когда вероятности состояний природы либо вообще не существуют, либо не подда­ются оценке даже приближенно. В этом случае используются так называемые критерии для выбора решения, характеризующие точку зрения на ситуацию лица, принимающего решения.

Существует значительное число воз­можных подходов для решения данной задачи. Опишем лишь некоторые основные.

Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разум­ным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оп­тимальной считается стратегия, при которой гаранти­руется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой»

.

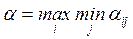Если руководствоваться этим критерием, олицетво­ряющим «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Очевидно, такой подход - «перестраховочный», естественный для того, кто очень боится проиграть, - не является единственно возмож­ным, но как крайний случай он заслуживает рас­смотрения.

Критерий минимаксного риска Сэвиджа. Этот критерий — тоже крайне пессимистический, но при вы­боре оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оп­тимальной та стратегия, при которой величина риска в наихудших условиях минимальна

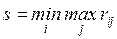
Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но само понятие «пессимизм» здесь пони­мается по-другому.

Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руко­водствоваться ни крайним пессимизмом («всегда рас­считывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Согласно этому критерию выбирается стратегия из условия

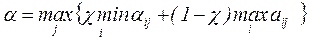
где 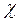— «коэффициент пессимизма», выбираемый меж­ду нулем и единицей.

При 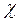= 1 критерий Гурвица превращается в критерий Вальда; при 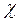= 0 - в кри­терий «крайнего оптимизма», рекомендующий выбрать ту стратегию, при которой самый большой выигрыш в строке максимален. При 0 < 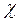< 1 получается нечто среднее между тем и другим. Коэффициент 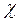выбира­ется из субъективных соображений - чем опаснее си­туация, чем больше мы хотим в ней «подстраховать­ся», чем менее, наша склонность к риску, тем ближе к единице выбирается .

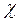Понятно, что выбор решения в условиях неопределенности условен, субъекти­вен. И все же в какой-то (ограниченной) мере мате­матические методы полезны и тут. Прежде всего, они позволяют привести игру с природой к матричной фор­ме, что далеко не всегда бывает просто, особенно когда стратегий много (в наших примерах их было очень мало). Кроме того, они позволяют заменить простое лицезрение матрицы выигрышей (или рисков), от ко­торого, когда матрица велика, может просто «зарябить в глазах», последовательным численным анализом си­туации с разных точек зрения, выслушать рекоменда­ции каждой из них и, наконец, остановиться на чем-то определенном. Это аналогично обсуждению вопроса с различных позиций, а в споре, как известно, рождает­ся истина.

Если рекомендации, вытекающие из различных критериев, совпадают, то можно смело выбрать рекомендуемое решение: оно скорее всего «не подведет. В противном случае необходимо воспользоваться здравым смыслом.

Не надо забывать, что в любых задачах обоснования решений некоторый

произвол неизбежен — хо­тя бы при построении ма­тематической модели, вы­боре показателя эффектив­ности.

Рассмотрим пример «игры с природой» 4×3, матрица выигры­шей которой (а_ij) дана в таблице 12 и, пользуясь крите­риями Вальда, Сэвиджа и Гурвица (при 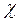= 0,6), определим оптимальное решение.

Таблица 12

	Н1	Н2	Н3
А1
А2
А3
А4

Для нахождения оптимальной стратегии по критерию Вальда подсчитаем ми­нимумы по строкам (см. таблицу 13) и выберем ту стратегию, при которой минимум строки максимален (равен 25). Это — стратегия А₃.

Таблица 13

	Н1	Н2	Н3	αi
А1
А2
А3
А4

Для нахождения оптимальной стратегии по критерию Сэвиджа перейдем от матрицы выигрышей (таблица 13) к матрице рисков (таблица 14), в правом дополнительном столбце записывая максимальное в строке значение риска r_i.

Таблица 14

	Н1	Н2	Н3	ri
А1
А2
А3
А4

Из чисел правого столбца минимальное значение r_i = 60 соответствует стратегиям А₂ и А₃. Они обе оптимальны по Сэвиджу.

Для нахождения оптимальной стратегии по критерию Гурвица (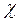 =0,6) перепишем таблицу 12, но на этот раз в трех правых дополнительных столбцах новой таблицы 15 поставим соответственно минимум строки α_i, ее максимум ω_i и величину 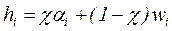, округленную до целых единиц (см. таблицу 15).

Таблица 15

	Н1	Н2	Н3	αi	wi	hi
А1
А2
А3
А4

Максимальное значение h_i = 47 соответствуем стра­тегии A₃.

Дата добавления: 2014-11-29