Колебания синхронной машины

Рассмотрим сначала случай, когда амплитуда колебаний угла нагрузки мала. При этом дифференциальное уравнение движения ротора является линейным и имеет простое решение, позволяющее выяснить существенные особенности колебательного процесса синхронной машины. Для изучения этого вопроса составим уравнение вращающих моментов синхронной машины при ее колебаниях и для определенности будем иметь в виду режим генератора, хотя получаемые результаты будут действительны и для двигателя.

Вращающие моменты, действующие при колебаниях. Электромагнитный момент выражается равенством

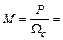
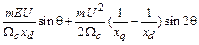. (9.1.)

Пусть колебания совершаются около значения угла соответствующего состоянию равновесия, когда электромагнитный момент 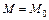уравновешивается внешним вращающим моментом, приложенным к валу машины. Тогда при колебаниях:

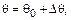(9.2.)

где 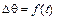представляет собой переменную величину отклонения угла при колебаниях машины.

Подставим 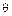из (9.2) в (9.1) и ввиду малости 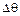положим, что

= ()= +

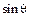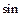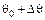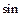
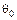
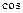
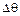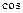
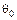
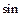
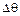
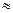
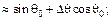
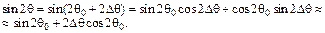
Тогда вместо (9.1) получим

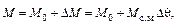(9.3.)

где

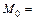
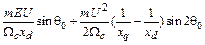(9.4.)

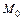в (9.4) представляет собой значение 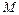по формуле (9.1) при 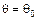, а

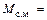
(9.5)

является коэффициентом синхронизирующего момента. При этом принимается, что ввиду малой амплитуды колебаний скорость вращения = .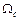

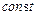Так как 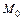уравновешивается приложенным к валу внешним моментом, то достаточно учесть лишь второй член (9.3), который представляет собой синхронизирующий момент

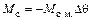(9.6)

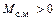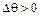и играет при этом роль, аналогичную упругой силе колеблющейся пружины с грузом. Знак минус в выражении (9.6) введен в связи с тем, что при и момент 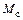действует на вал тормозящим образом.

Необходимо отметить, что выражение (9.5) для 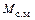действительно только при чрезвычайно медленных изменениях угла 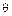, когда можно пренебречь электромагнитными переходными процессами в обмотках машины. В действительности скорость колебаний конечна, и

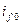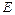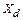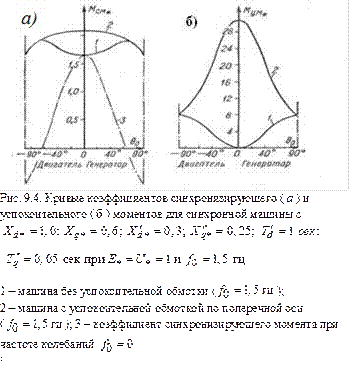
поэтому в обмотках индуктора возникают такие же дополнительные апериодические токи, как и при внезапном коротком замыкании. Действие этих токов подобно действию тока возбуждения , создаваемого напряжением возбудителя, что эквивалентно некоторому увеличению или уменьшению в равенстве (9.5). Вследствие этого при переходных процессах и, в частности, при колебаниях значение 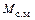в действительности больше значения, определяемого равенством (9.5). На рис. 9.4, а в качестве примера приведены кривые 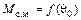для явнополюсной машины при колебаниях с частотой 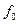= 1,5 Гц. Там же для сравнения изображена кривая 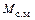построенная по равенству (9.5) для случая, если бы колебания совершались чрезвычайно медленно ( 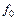= 0). На рис. 9.4, 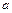отложена относительная величина коэффициента синхронизирующего момента

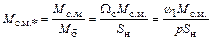(9.7)

Инерционный вращающий момент

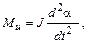
где – момент инерции вращающихся частей и

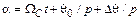
представляет собой угловую координату движения ротора. Угол 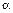выражается в геометрических единицах угла, и поэтому электрические углы 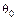и 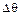разделены на число пар полюсов 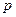. Таким образом,

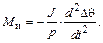(9.8)

Успокоительный момент 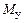при малых скольжениях 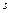, как и всякий асинхронный момент, пропорционален :

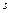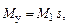
где 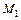– коэффициент пропорциональности, имеющий размерность момента.

Величина 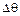изменяется вследствие изменения скольжения, и

,

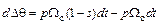где первый член представляет собой угол поворота вектора 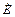за время 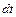, а второй – угол поворота вектора 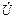за это же время.

Отсюда

.

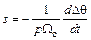Поэтому

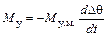, (9.9)

где – коэффициент успокоительного момента.

Можно показать, что в случае, когда ротор синхронной машины в электрическом отношении полностью симметричен, как и ротор асинхронной машины, для 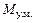действительно выражение для вращающего момента асинхронной машины, если заменить в нем 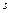на отношение 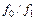. В действительности такая симметрия отсутствует, и поэтому 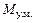зависит от положения осей симметрии ротора относительно волны поля реакции якоря, т. е. от угла .

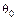Как следует из равенства (9.9), 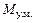имеет размерность момента, умноженного на время. При переходе к относительным единицам за базисное следует принимать значение 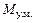при 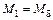, и тогда

.

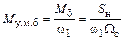На рис.9.4, б приведены относительные безразмерные значения коэффициента успокоительного момента

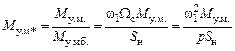. (9.10)

Уравнение моментов и его решение. Согласно изложенному, уравнение моментов при колебаниях имеет вид

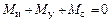
или, согласно (9.6), (9.8) и (9.9),

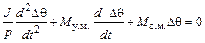. (9.11)

Решением уравнения (9.11) является

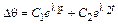, (9.12)

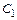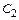где и – постоянные интегрирования, а 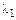и 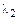– корни характеристического уравнения

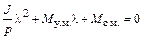
имеющие вид

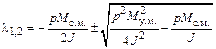, (9.13)

Первый член под корнем выражения (9.13) обычно значительно меньше второго, и поэтому квадратный корень представляет собой мнимое число. Это и является условием возникновения колебательного процесса, так как при вещественном корне изменение 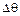будет апериодическим.

Согласно сказанному, вместо (9.13) можно написать

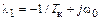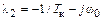; , (9.14)

где

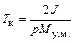(9.15)

представляет собой постоянную времени затухания колебаний, а

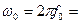
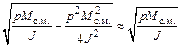, (9.16)

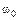– угловую частоту свободных, или собственных, колебаний син-хронной машины.

При подстановке 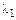и 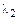из (9.14) в (9.12) получим

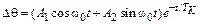, (9.17)

где 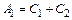и 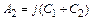– новые постоянные интегрирования, определяемые из начальных условий. Например, в случае, соответствующем рис. 9.2,

;

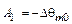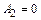
и поэтому

.

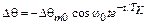Согласно равенствам (9.15) и (9.17), колебания затухают тем быстрее, чем больше 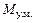. При 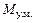=0 постоянная времени и колебания являются незатухающими.

Частота свободных колебаний. Вместо обычно рассматривают так называемую инерционную постоянную

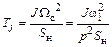, (9.18)

которая равна отношению удвоенной кинетической энергии вращающихся масс при 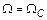к номинальной полной мощности 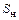. Физически 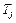означает время, в течение которого агрегат достигнет номинальной скорости на холостом ходу при пуске в ход, если к валу приложен постоянный вращающий момент

.

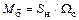Маховой момент 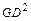равен массе вращающихся частей 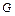, умноженной на квадрат диаметра инерции 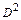, и в системе СИ выражается в 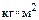. В этой системе единиц

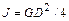. (9.19)

Поэтому также

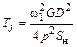. (9.20)

Значения 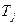приведены в табл..

Если в выражение (9.16) подставить значение из (9.18) и учесть равенства (9.7) и (9.10), то получим

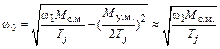. (9.21)

Частота собственных колебаний

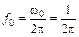
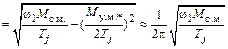. (9.22)

Например, для машины с параметрами, указанными в подписи к рис. 9.4, согласно этому рисунку, при 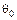= 20° имеем 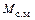= 2,15 и

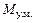= 28. Если 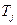=7,3 с, то по формуле (9.22) получим

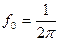
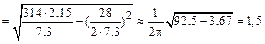Гц.

Период собственных колебаний при этом

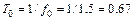сек.

Самораскачивание синхронной машины. В случае когда 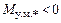и поэтому на основании выражения (9.15) 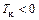, в соответствии с (9.17) сколь угодно малые колебания, возникшие в результате каких-либо возмущений, будут не затухать, а возрастать по амплитуде. Такие случаи возникают на практике в маломощных синхронных машинах, не имеющих успокоительной обмотки, при работе параллельно с сетью на холостом ходу или при весьма малой нагрузке. При этом 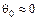и, согласно рис. 9.4, б, также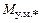 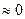. Однако кривые рис. 9.4, б учитывают только успокоительный момент, который создается токами, индуктируемыми в обмотках ротора, при сопротивлении обмотки якоря 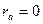. Как показывает более подробный анализ этого вопроса, при 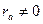создается еще небольшая дополнительная составляющая 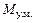, которая отрицательна и по абсолютной величине тем больше, чем больше 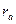. При этом в области 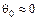результирующая величина 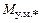у малых машин, которые имеют повышенные значения 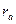, становится отрицательной и возникают самопроизвольные колебания, или так называемое самораскачивание машины.

Амплитуда колебаний, достигнув определенного значения, обычно стабилизируется в результате наличия нелинейных зависимостей. У машин с 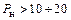кВт самораскачивания обычно не наблюдается как ввиду малости 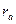, так и в результате того, что и при расслоенных полюсах в сердечнике ротора индуктируются вихревые токи, создающие положительный успокоительный момент.

Дата добавления: 2014-11-29