
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамическая устойчивость синхронной машины
|
|
|
|
Под динамической устойчивостьюсинхронной машины понимается ее способность сохранять синхронный режим параллельной работы с сетью при больших и резких возмущениях режима ее работы (короткие замыкания в сети и пр.). Устойчивость работы при этих условиях зависит как от величины возмущения и его длительности, так и от параметров машины, значения ее предшествующей нагрузки и прочих условий. В большинстве случаев при таких возмущениях возникают колебания или качания ротора с большой амплитудой. Нередко возникающий при таких возмущениях режим работы является неустойчивым и машина выпадает из синхронизма.
Вопросы, связанные с динамической устойчивостью, весьма сложны и рассматриваются подробнее в специальных курсах. Ниже дается лишь понятие о динамической устойчивости.
ЭДС за переходным сопротивлением и угловая характеристика мощности при переходных режимах. При резких изменениях режима работы синхронной машины, как и при внезапных коротких замыканиях, в обмотках индуктора возникают добавочные апериодические токи, в результате чего ЭДС 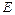 , индуктируемая в обмотке якоря, увеличивается и угловая характеристика активной мощности, выражаемая равенством (9.4), изменяется. Как видно из (9.4), при этих условиях машина в состоянии развить большую электрическую мощность. Хотя равенством (9.4) можно пользоваться и при переходных режимах, но это неудобно, так как при этом каждый раз необходимо определять
, индуктируемая в обмотке якоря, увеличивается и угловая характеристика активной мощности, выражаемая равенством (9.4), изменяется. Как видно из (9.4), при этих условиях машина в состоянии развить большую электрическую мощность. Хотя равенством (9.4) можно пользоваться и при переходных режимах, но это неудобно, так как при этом каждый раз необходимо определять 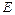 с учетом влияния апериодических токов в обмотках ин-дуктора. Поэтому целесообразно такое изменение соотношения (9.4), чтобы в него входили величины, которые при резких изменениях режима остаются неизменными.
с учетом влияния апериодических токов в обмотках ин-дуктора. Поэтому целесообразно такое изменение соотношения (9.4), чтобы в него входили величины, которые при резких изменениях режима остаются неизменными.
Как было установлено ранее, при резких изменениях режима в
обмотках возбуждения и успокоительной возникают апериодические токи, затухающие с постоянными времени 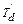 и
и 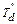 . Так как период собственных колебаний
. Так как период собственных колебаний 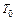 =
= 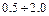 сек,
сек, 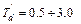 сек и
сек и 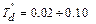 сек, то отсюда следует, что быстро затухающие апериодические токи затухают уже в самом начале первого периода колебаний и поэтому мало влияют на эти колебания. Следовательно, этими токами можно пренебречь. Однако
сек, то отсюда следует, что быстро затухающие апериодические токи затухают уже в самом начале первого периода колебаний и поэтому мало влияют на эти колебания. Следовательно, этими токами можно пренебречь. Однако 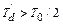 , поэтому медленно затухающие апериодические токи ротора в течение первого полупериода колебаний изменяются мало и в течение этого времени их можно считать постоянными. Изложенное равнозначно предположению, что в течение начального периода колебаний
, поэтому медленно затухающие апериодические токи ротора в течение первого полупериода колебаний изменяются мало и в течение этого времени их можно считать постоянными. Изложенное равнозначно предположению, что в течение начального периода колебаний 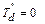 и
и 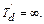 Это соответствует случаю, когда успокоительная обмотка отсутствует, а обмотка возбуждения является сверхпроводящей и поэтому ее потокосцепление постоянно. Сопротивление успокоительной обмотки по поперечной оси
Это соответствует случаю, когда успокоительная обмотка отсутствует, а обмотка возбуждения является сверхпроводящей и поэтому ее потокосцепление постоянно. Сопротивление успокоительной обмотки по поперечной оси 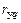 также велико, и поэтому можно положить, что
также велико, и поэтому можно положить, что 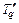 = 0. Исходя из этих положений, можно преобразовать равенство (9.4), которое будет действительно для начального периода колебаний при резких изменениях режима работы синхронной машины.
= 0. Исходя из этих положений, можно преобразовать равенство (9.4), которое будет действительно для начального периода колебаний при резких изменениях режима работы синхронной машины.
Учитывая, что 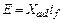 , для установившегося режима действительно соотношение
, для установившегося режима действительно соотношение
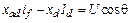 . (9.23)
. (9.23)
Оно действительно и для начального периода резкого нарушения режима, если учесть увеличение 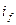 в результате возникновения свободной апериодической составляющей этого тока.
в результате возникновения свободной апериодической составляющей этого тока.
С другой стороны, условие постоянства потокосцепления обмотки возбуждения 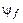 можно написать в следующем виде:
можно написать в следующем виде:
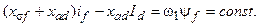
Отсюда
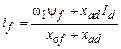 ,
,
и это выражение также действительно как до, так и после резкого нарушения режима. Подставив это значение 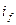 в (9.23), находим
в (9.23), находим
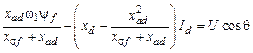 (9.24)
(9.24)
Обозначим первый член этого выражения, который вследствие постоянства потокосцепления 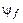 также постоянен, через
также постоянен, через 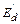 . С другой стороны, коэффициент второго члена представляет собой переход-
. С другой стороны, коэффициент второго члена представляет собой переход-
ное сопротивление 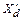 . Поэтому вместо (9.24) получим
. Поэтому вместо (9.24) получим
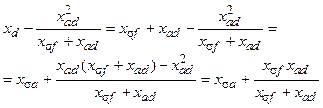
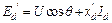 , (9.25)
, (9.25)
причем 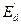 =
=  и соотношение (9.25) также действительно до и после нарушения режима.
и соотношение (9.25) также действительно до и после нарушения режима.
Значение ЭДС 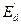 , называемой ЭДС за переходным сопротивлением
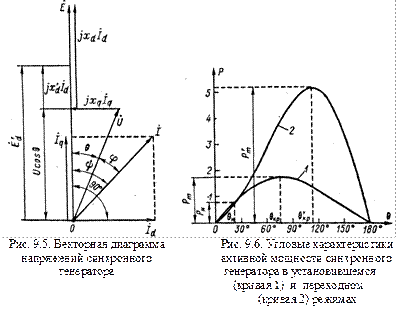
, называемой ЭДС за переходным сопротивлением 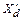 , можно найти, построив векторную диаграмму ЭДС по данным предшествующего режима (рис. 9.5). Построив на этой диаграмме векторы
, можно найти, построив векторную диаграмму ЭДС по данным предшествующего режима (рис. 9.5). Построив на этой диаграмме векторы  и
и 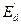 , получим видоизмененную диаграмму, отличающуюся от обычной только заменой
, получим видоизмененную диаграмму, отличающуюся от обычной только заменой 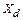 на
на 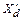 и
и 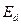 на
на 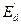 . Поэтому и выражение для угловой характеристики получим путем такой же замены в соотношении (7.4). Таким образом, при резких нарушениях режима в начальный период колебаний имеем
. Поэтому и выражение для угловой характеристики получим путем такой же замены в соотношении (7.4). Таким образом, при резких нарушениях режима в начальный период колебаний имеем
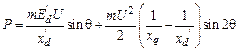 . (9.26)
. (9.26)
 ТТак как
ТТак как 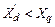 , то множитель перед
, то множитель перед 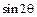 в данном случае отрицателен. На рис. 9.6 представлены зависимости
в данном случае отрицателен. На рис. 9.6 представлены зависимости  по (7.4) (кривая 1) и по (9.26) (кривая 2) для явнополюсной машины с
по (7.4) (кривая 1) и по (9.26) (кривая 2) для явнополюсной машины с 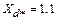 ,
,  ,
, 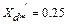 при
при 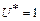 , когда машина в установившемся режиме работала с номинальной нагрузкой (
, когда машина в установившемся режиме работала с номинальной нагрузкой (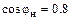 (инд.),
(инд.), 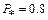 ,
, 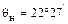 ), чему соответствует
), чему соответствует 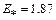 и
и 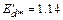 .
.
Из рис. 9.6 следует, что в переходном режиме машина при таком же значении 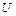 может нести значительно большую нагрузку, тем большую, чем меньше
может нести значительно большую нагрузку, тем большую, чем меньше 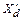 . Поэтому, чем меньше
. Поэтому, чем меньше 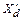 , тем больше динамическая устойчивость машины.
, тем больше динамическая устойчивость машины.
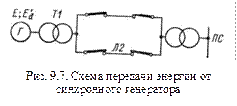
Понятие о динамической устойчивости. Рассмотрим случай (рис. 9.7), когда генератор Г, эквивалентный мощной электростанции, работает через трансформаторы 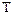 1 и
1 и 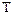 2 и две параллельные линии передачи Л1 и Л2 на приемную систему ПС с
2 и две параллельные линии передачи Л1 и Л2 на приемную систему ПС с 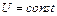 . При установившемся режиме генератор работает в точке 1 угловой характеристики
. При установившемся режиме генератор работает в точке 1 угловой характеристики 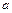 рис. 9.8, определяемой равенством (7.4), причем в данном случае параметры
рис. 9.8, определяемой равенством (7.4), причем в данном случае параметры 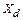 ,
, 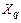 ,
, 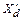 включают в себя также индуктивные сопротивления трансформаторов линии передачи.
включают в себя также индуктивные сопротивления трансформаторов линии передачи.
В точке 1 мощность генератора 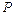 равна мощности
равна мощности 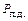 , развиваемой турбиной.
, развиваемой турбиной.
Допустим теперь, что в результате какой-либо неисправности одна из параллельных линий отключается. В результате такого динамического нарушения режима наступает переходный процесс, в начальной стадии которого величина 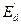 , определяемая параметрами и другими величинами исходного режима, остается постоянной. При этом будет
, определяемая параметрами и другими величинами исходного режима, остается постоянной. При этом будет
справедливо соотношение (9.26), но вследствие отключения одной линии 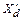 увеличится и в результате этого угловая характеристика переходного режима б рис. 9.8, может пойти ниже характеристики
увеличится и в результате этого угловая характеристика переходного режима б рис. 9.8, может пойти ниже характеристики 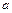 , несмотря на отмеченную выше способность машины развивать в переходном режиме при тех же
, несмотря на отмеченную выше способность машины развивать в переходном режиме при тех же 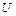 и
и 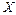 большую мощность. Угол
большую мощность. Угол 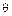 вследствие инерции мгновенно измениться не может, и поэтому непосредственно вслед за отключением линии генератор переходит на работу в точку 2 характеристики
вследствие инерции мгновенно измениться не может, и поэтому непосредственно вслед за отключением линии генератор переходит на работу в точку 2 характеристики 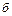 . Так как мощность турбины остается постоянной, то при этом
. Так как мощность турбины остается постоянной, то при этом 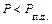 , поэтому ротор будет ускоряться и угол
, поэтому ротор будет ускоряться и угол 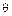 будет расти. В точке 3 наступит равновесие мощностей
будет расти. В точке 3 наступит равновесие мощностей 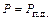 и вращающих моментов, но угловая скорость
и вращающих моментов, но угловая скорость 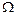 будет больше синхронной
будет больше синхронной  , и поэтому
, и поэтому 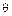 продолжает увеличиваться. Вправо от точки 3 будет
продолжает увеличиваться. Вправо от точки 3 будет 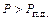 , поэтому ротор будет тормозиться,
, поэтому ротор будет тормозиться, 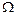 – уменьшаться и на рис. 9.8,
– уменьшаться и на рис. 9.8, 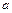 в некоторой точке 4 скорость уменьшится до синхронной
в некоторой точке 4 скорость уменьшится до синхронной 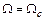 .
.
Положение точки 4 определяется равенством площадей заштрихованных треугольников 123 и 345, т. е. 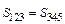 (правило площадей). Действительно, длины линий штриховки этих треугольников пропорциональны неуравновешенному синхронизирующему моменту:
(правило площадей). Действительно, длины линий штриховки этих треугольников пропорциональны неуравновешенному синхронизирующему моменту:

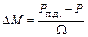
и работа 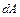 , совершаемая этим моментом при изменении угла на
, совершаемая этим моментом при изменении угла на 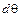 , равная
, равная
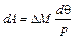 ,
,
идет на сообщение ротору во время его ускорения добавочной кинетической энергии этой же величины. Поэтому на участке кривой 1 – 3 ротор получает добавочную кинетическую энергию
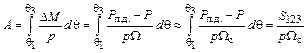 .
.
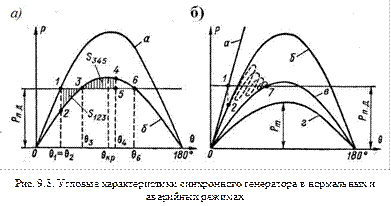
Здесь мы положили  так как эти величины мало отличаются друг от друга.
так как эти величины мало отличаются друг от друга.
Аналогично при торможении ротора на участке 3 – 4 его кинетическая энергия уменьшается на величину  , и поэтому скорость ротора достигнет синхронной, когда
, и поэтому скорость ротора достигнет синхронной, когда  .
.
Таким образом, в точке 4 будет 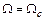 , но так как
, но так как 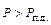 , то торможение ротора продолжается,
, то торможение ротора продолжается, 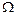 становится меньше
становится меньше 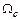 и
и 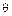 уменьшается. При этом режим работы меняется от точки 4 к точке 3, в точке 3
уменьшается. При этом режим работы меняется от точки 4 к точке 3, в точке 3 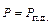 и торможение прекращается, но при этом
и торможение прекращается, но при этом 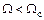 , уменьшение
, уменьшение 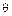 поэтому будет продолжаться и режим меняется от точки 3 к точке 2. На этом участке
поэтому будет продолжаться и режим меняется от точки 3 к точке 2. На этом участке 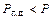 поэтому будет происходить ускорение ротора,
поэтому будет происходить ускорение ротора, 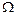 будет расти, но уменьшение
будет расти, но уменьшение 
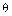 будет продолжаться до тех пор, пока в точке 2 не станет
будет продолжаться до тех пор, пока в точке 2 не станет 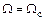 . Этим заканчивается первый период колебаний ротора и угла
. Этим заканчивается первый период колебаний ротора и угла 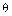 от
от 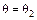 до
до 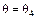 и обратно до
и обратно до 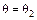 . После этого ротор снова начинает ускоряться, рассмотренный цикл колебаний повторяется и наступают незатухающие колебания ротора с колебаниями
. После этого ротор снова начинает ускоряться, рассмотренный цикл колебаний повторяется и наступают незатухающие колебания ротора с колебаниями 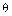 в диапазоне
в диапазоне 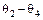 . Машина при этом из синхронизма не выпадает, хотя очевидно, что наибольший угол
. Машина при этом из синхронизма не выпадает, хотя очевидно, что наибольший угол 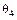 может быть больше
может быть больше 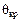 .
.
К заключению о возникновении незатухающих колебаний мы пришли потому, что полагали 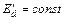 и неизменность в связи с этим характеристики б рис. 9.8,
и неизменность в связи с этим характеристики б рис. 9.8, 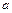 во время колебаний и, кроме того, пренебрегли успокоительным моментом
во время колебаний и, кроме того, пренебрегли успокоительным моментом 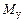 , возникающим в результате того, что
, возникающим в результате того, что 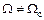 . В действительности даже при предположении
. В действительности даже при предположении 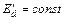 момент
момент 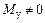 и машина развивает мощность также за счет этого момента. Поэтому при движении от точки 2 на рис. 9.8,
и машина развивает мощность также за счет этого момента. Поэтому при движении от точки 2 на рис. 9.8, 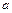 к точке 4, когда
к точке 4, когда 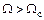 и
и  (режим асинхронного генератора), характеристика
(режим асинхронного генератора), характеристика  пойдет несколько выше кривой б, ускорение на участке 2 – 3 будет слабее, а торможение на участке 3 – 4 – сильнее и в результате угол
пойдет несколько выше кривой б, ускорение на участке 2 – 3 будет слабее, а торможение на участке 3 – 4 – сильнее и в результате угол 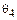 будет несколько меньше. Далее, при движении от точки 4 к точке 2, когда
будет несколько меньше. Далее, при движении от точки 4 к точке 2, когда 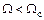 и
и 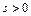 (режим асинхронного двигателя), характеристика
(режим асинхронного двигателя), характеристика 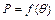 пойдет ниже кривой б, вследствие этого на участке 4 – 3 торможение вниз от
пойдет ниже кривой б, вследствие этого на участке 4 – 3 торможение вниз от 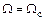 будет слабее, а на участке 3 – 2 ускорение будет сильнее и поэтому равенство
будет слабее, а на участке 3 – 2 ускорение будет сильнее и поэтому равенство 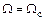 после первого периода колебаний наступит правее точки 2. Таким образом, под воздействием
после первого периода колебаний наступит правее точки 2. Таким образом, под воздействием 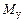 размах, или амплитуда, колебаний будет непрерывно уменьшаться до тех пор, пока эти колебания не затухнут полностью и при
размах, или амплитуда, колебаний будет непрерывно уменьшаться до тех пор, пока эти колебания не затухнут полностью и при 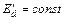 не наступит установившийся режим работы в точке 3, когда
не наступит установившийся режим работы в точке 3, когда 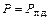 . Характер колебаний при этом имеет вид кривых на рис. 9.2 и 9.3.
. Характер колебаний при этом имеет вид кривых на рис. 9.2 и 9.3.
На самом деле предположение 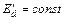 с достаточной точностью действительно только для первого полупериода колебаний, от точки 2 до точки 4 на рис. 9.8,
с достаточной точностью действительно только для первого полупериода колебаний, от точки 2 до точки 4 на рис. 9.8, 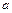 . В дальнейшем наступает заметное затухание всплеска тока возбуждения
. В дальнейшем наступает заметное затухание всплеска тока возбуждения 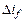 , вызванного динамическим нарушением режима, и поэтому
, вызванного динамическим нарушением режима, и поэтому 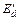 будет уменьшаться. Вследствие этого ординаты кривой б будут непрерывно уменьшаться и при
будет уменьшаться. Вследствие этого ординаты кривой б будут непрерывно уменьшаться и при 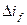 =0 характеристика
=0 характеристика 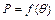 изобразится в виде кривой в на рис. 9.8, б, которая соответствует равенству (9.4) и расположена ниже кривой
изобразится в виде кривой в на рис. 9.8, б, которая соответствует равенству (9.4) и расположена ниже кривой 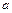 , так как при отключении одной линии на схеме рис. 9.7
, так как при отключении одной линии на схеме рис. 9.7 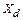 и
и 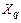 увеличатся. Поэтому колебания в действительности происходят вдоль штриховой кривой рис.9.8, б и установившийся режим наступает в точке 7 кривой в. Колебания при этом также имеют характер, изображенный на рис. 9.2 и 9.3. Однако если, согласно выражению (7.4), установившемуся режиму вместо кривой в рис. 9.8, б будет соответствовать кривая г этого же рисунка, то машина, сохраняя синхронизм в течение первого периода колебаний, выйдет из синхронизма в течение последующих циклов колебаний, так как максимальная развиваемая мощность генератора
увеличатся. Поэтому колебания в действительности происходят вдоль штриховой кривой рис.9.8, б и установившийся режим наступает в точке 7 кривой в. Колебания при этом также имеют характер, изображенный на рис. 9.2 и 9.3. Однако если, согласно выражению (7.4), установившемуся режиму вместо кривой в рис. 9.8, б будет соответствовать кривая г этого же рисунка, то машина, сохраняя синхронизм в течение первого периода колебаний, выйдет из синхронизма в течение последующих циклов колебаний, так как максимальная развиваемая мощность генератора 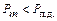 . Угол
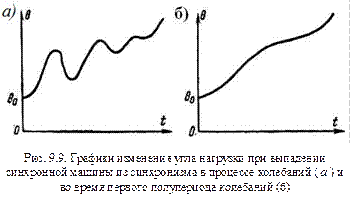
. Угол 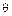 при этом будет беспредельно расти (рис. 9.9,
при этом будет беспредельно расти (рис. 9.9, 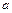 ).
).
Может случиться также, что кривая 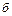 на рис.9.8,
на рис.9.8, 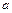 , будет располагаться настолько низко, что площадь
, будет располагаться настолько низко, что площадь 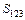 будет больше площади
будет больше площади 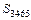 фигуры 3465, находящейся над прямой
фигуры 3465, находящейся над прямой 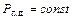 . Тогда площадь торможения
. Тогда площадь торможения 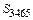 будет недостаточна и, хотя на участке 346 ротор тормозится, в точке б скорость
будет недостаточна и, хотя на участке 346 ротор тормозится, в точке б скорость 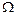 будет еще больше синхронной
будет еще больше синхронной 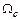 и угол
и угол 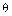 в точке 6 будет продолжать увеличиваться. Поэтому изменение режима будет происходить вправо от точки 6, при этом
в точке 6 будет продолжать увеличиваться. Поэтому изменение режима будет происходить вправо от точки 6, при этом 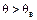 и
и 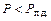 . В результате вновь наступит ускорение ротора, угол
. В результате вновь наступит ускорение ротора, угол 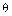 будет непрерывно расти, машина выпадет из синхронизма и перейдет в возбужденный асинхронный режим работы, когда генераторные режимы будут чередоваться с двигательными. В этом случае выпадение из синхронизма произойдет в первом цикле колебаний и характер функции
будет непрерывно расти, машина выпадет из синхронизма и перейдет в возбужденный асинхронный режим работы, когда генераторные режимы будут чередоваться с двигательными. В этом случае выпадение из синхронизма произойдет в первом цикле колебаний и характер функции 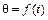 будет иметь вид рис.9.9, б.
будет иметь вид рис.9.9, б.
Выше мы предполагали, что ток возбуждения 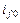 во время динамических нарушений не регулируется. Ясно, однако, что если в самом начале динамического нарушения
во время динамических нарушений не регулируется. Ясно, однако, что если в самом начале динамического нарушения 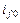 быстро увеличить, то
быстро увеличить, то 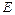 и
и 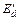 увеличатся и поэтому кривые
увеличатся и поэтому кривые 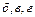 на рис. 9.9,
на рис. 9.9, 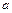 и
и 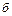 , расположатся выше. Во-первых, при этом уменьшится амплитуда колебаний угла
, расположатся выше. Во-первых, при этом уменьшится амплитуда колебаний угла 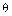 .
.
Во-вторых, при достаточно большом увеличении 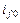 можно избежать выпадения машины из синхронизма.
можно избежать выпадения машины из синхронизма.
Кроме того, нетрудно заключить также, что целесообразно регулировать значение 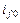 во время колебаний в зависимости от изменения
во время колебаний в зависимости от изменения 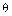 .
.
При этом, например, во время первого полупериода колебаний, при изменении угла 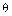 на рис. 9.8,
на рис. 9.8, 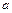 , от
, от 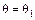 до
до 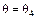 , надо
, надо 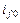 увеличивать, а во время второго полупериода, от точки 4 до точки 2, – уменьшать. При этом размах колебаний
увеличивать, а во время второго полупериода, от точки 4 до точки 2, – уменьшать. При этом размах колебаний 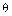 уменьшится.
уменьшится.
При подобном же регулировании 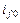 в последующих циклах колебаний можно достичь быстрого успокоения колебаний. Такое же регулирование возбуждения эффективно для уменьшения амплитуды вынуденных колебаний синхронных двигателей и генераторов, соединенных с поршневыми машинами.
в последующих циклах колебаний можно достичь быстрого успокоения колебаний. Такое же регулирование возбуждения эффективно для уменьшения амплитуды вынуденных колебаний синхронных двигателей и генераторов, соединенных с поршневыми машинами.
ЗАКЛЮЧЕНИЕ
Развитие производительных сил современного общества немыслимо без все возрастающего производства и потребления электрической энергии. Наиболее распространенными в настоящее время преобразователями механической энергии в электрическую являются синхронные генераторы. Совершенствование конструкции последних с целью улучшения энергетических показателей, увеличения срока службы и повышения надежности тесно связано с требованиями промышленности, открытиями фундаментальных наук, развитием теории электрических машин.
Создание высокоэкономичных и надежных электрических машин требует усовершенствования методов оптимизационных расчетов на основе физического и математического моделирования. В то же время для инженеров остается важным умение выделять главные факторы в сложных задачах проектирования и исследования электрических машин и, принимая обоснованные допущения, получать сравнительно простой вид решения, удобный для практического применения. Успехи инженеров-электромехаников в разработках новых и модификации уже выпускаемых электрических машин могут быть достигнуты только при глубоком знании теории электромеханических преобразователей.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 4054; Нарушение авторских прав?; Мы поможем в написании вашей работы!