
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции в точке
|
|
|
|
Теоретический курс
Введение в анализ. Дифференциальное исчисление функции одной переменной.
I курс, I семестр
Додаток 18
Додаток 17
Додаток 16
Додаток 15
Додаток 14
Додаток 13
Додаток 12
Додаток 11
Будова молекули хлорофилла
Додаток 10
Додаток 9
Додаток 8
Додаток 7
Додаток 6
Додаток 5
Додаток 4
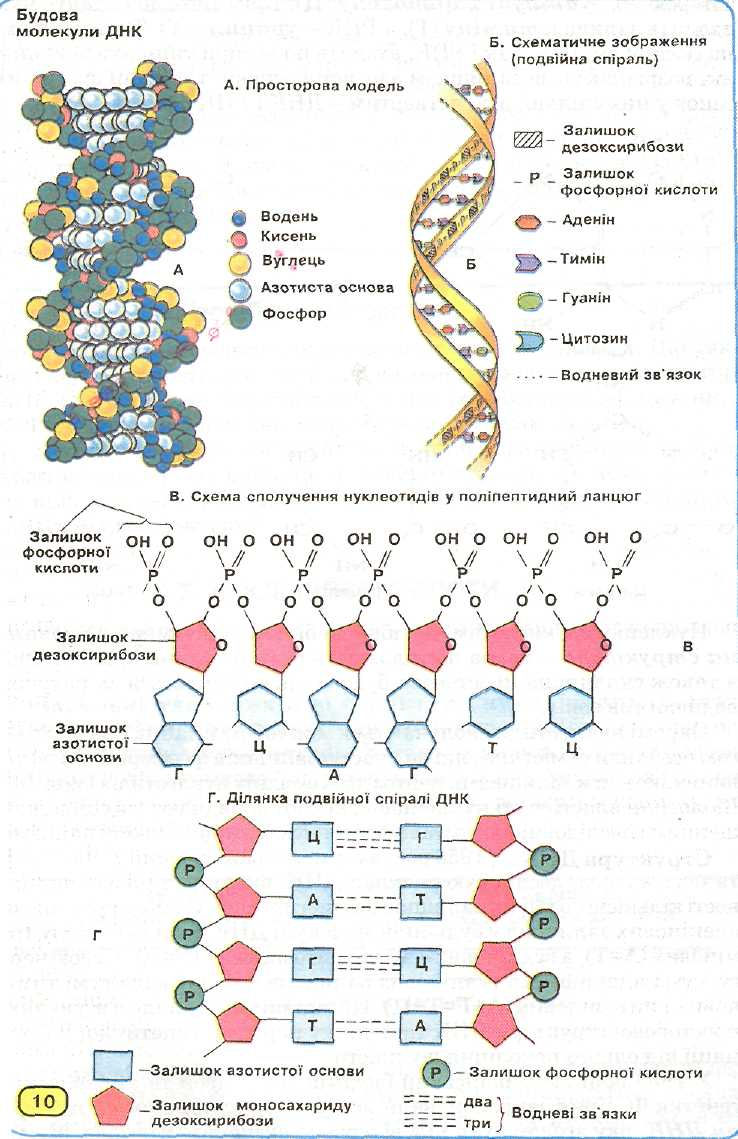
Оптичні прилади
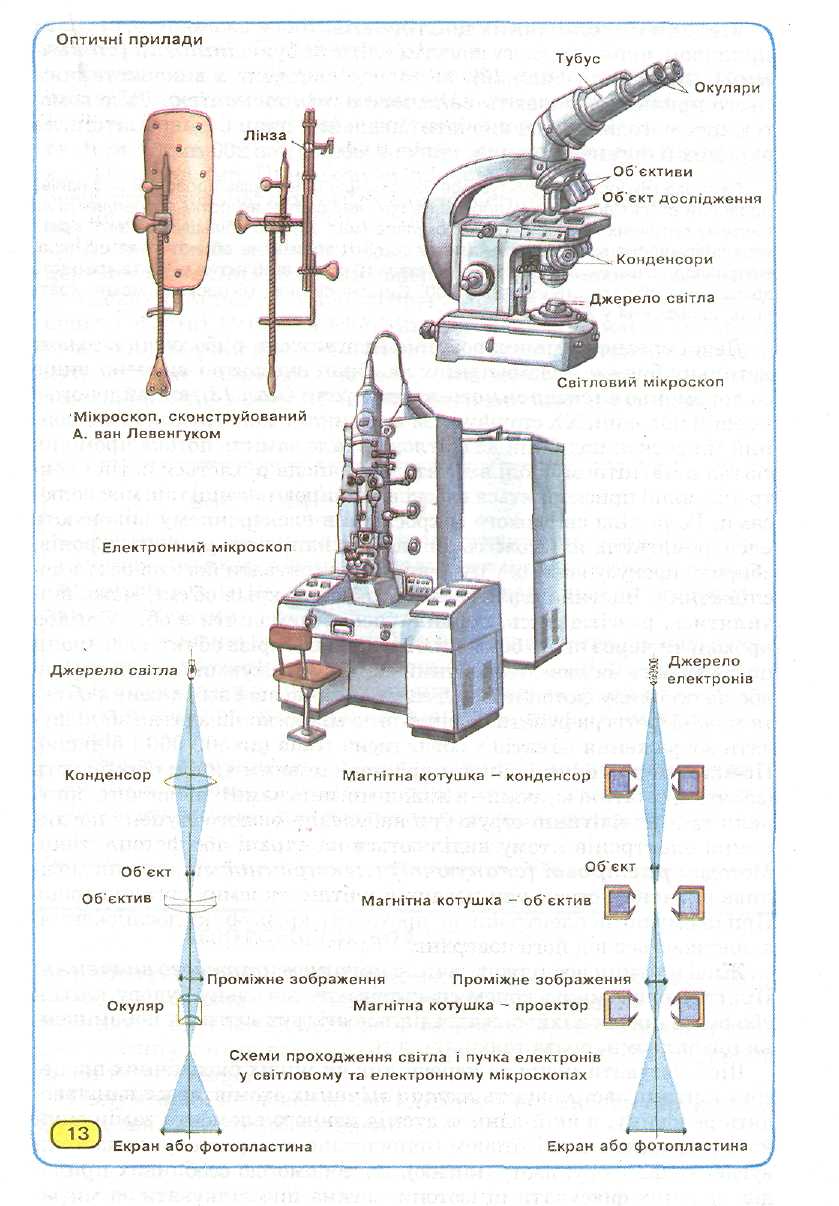
Поверхневий апарат тваринної клітини
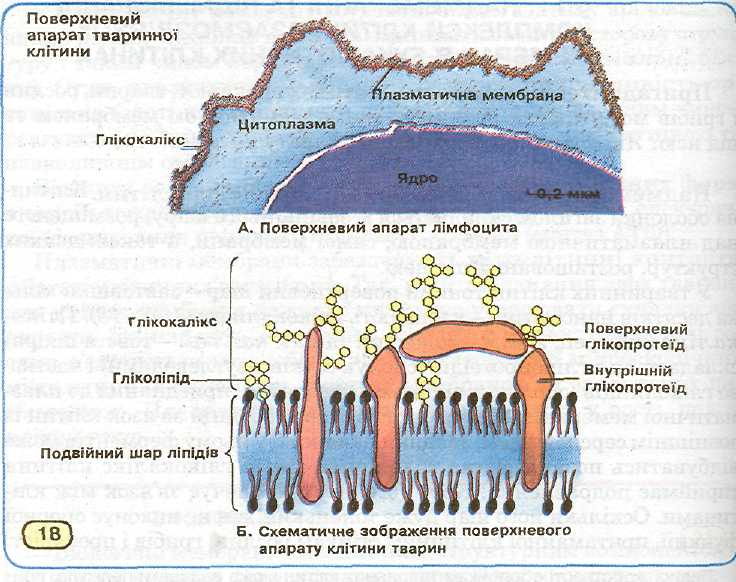
Схема будови клітинної мембрани
Схеми процесів піноцитозу та фагоцитозу
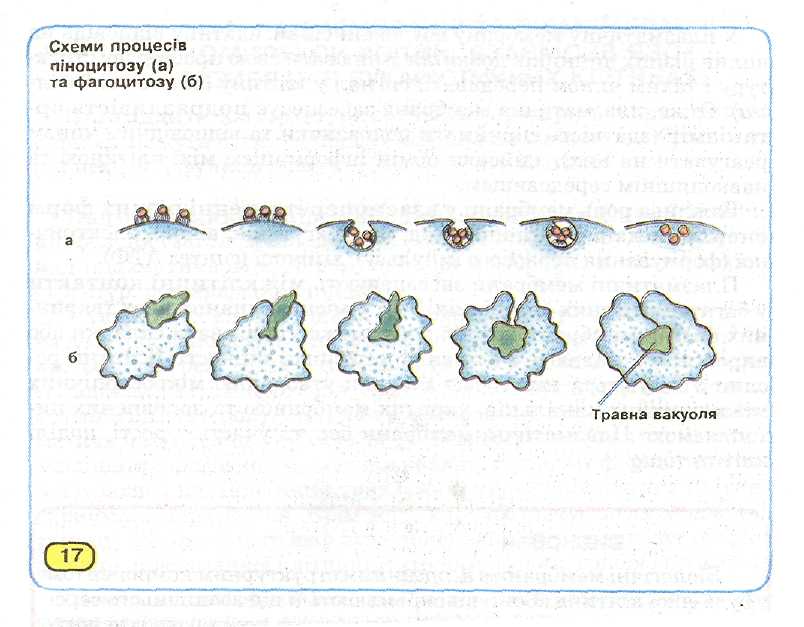
Схема мейозу
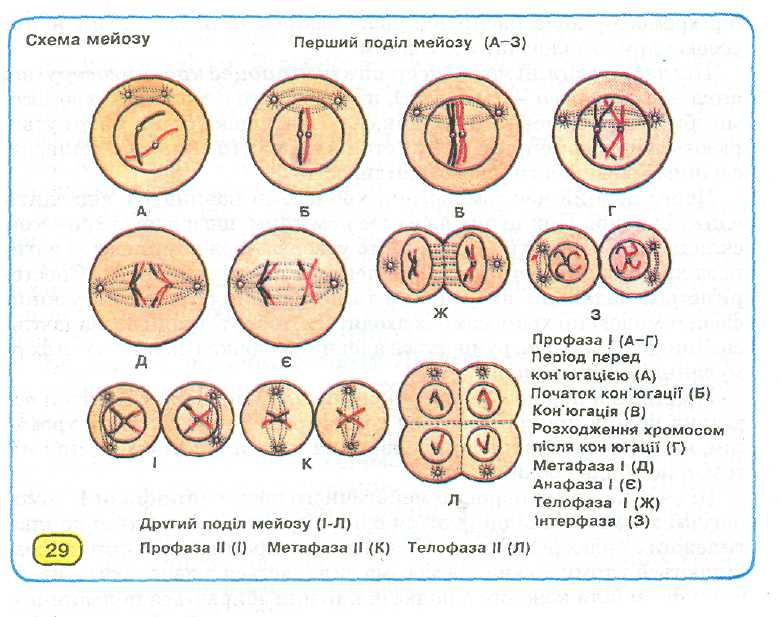
хлорофилл а хлорофилл b

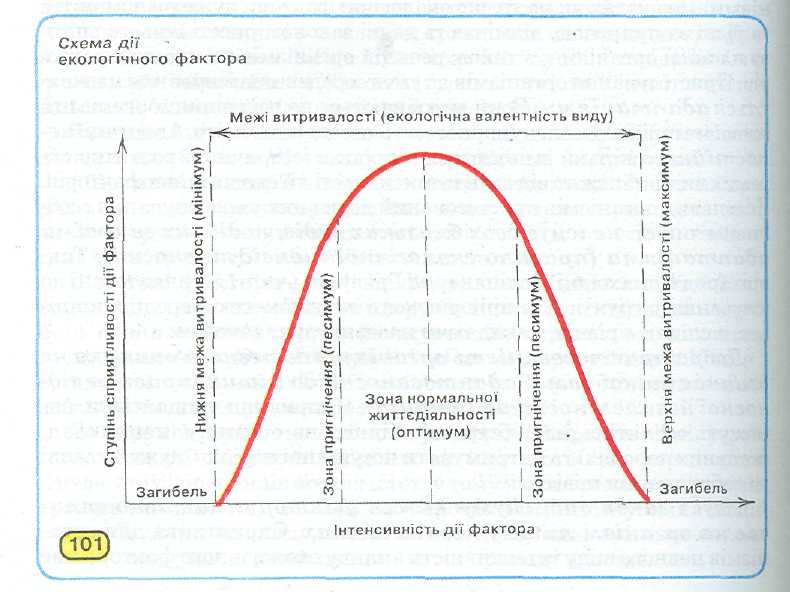
Схема дії екологічного фактора
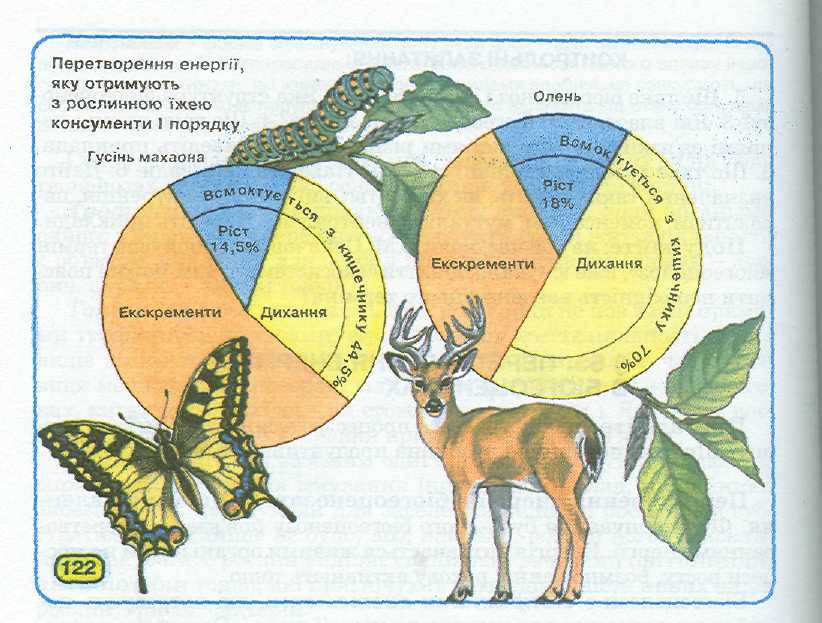
Перетворення енергії
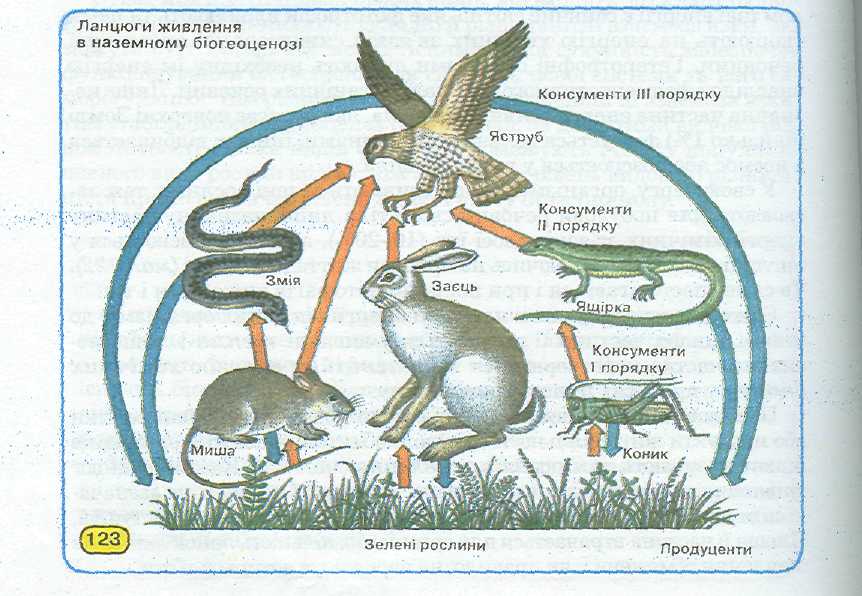
Ланцюги живлення в наземному біогеоценозі
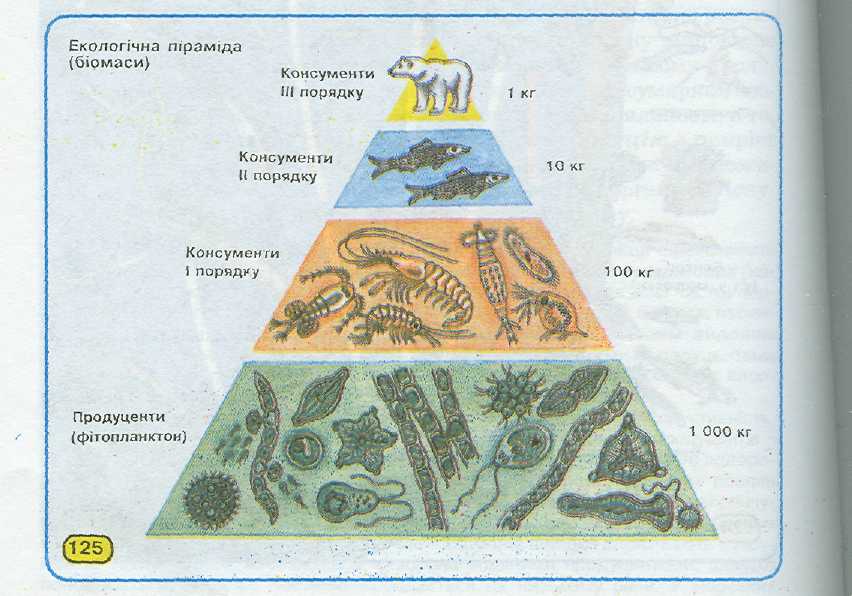
Екологічна піраміда
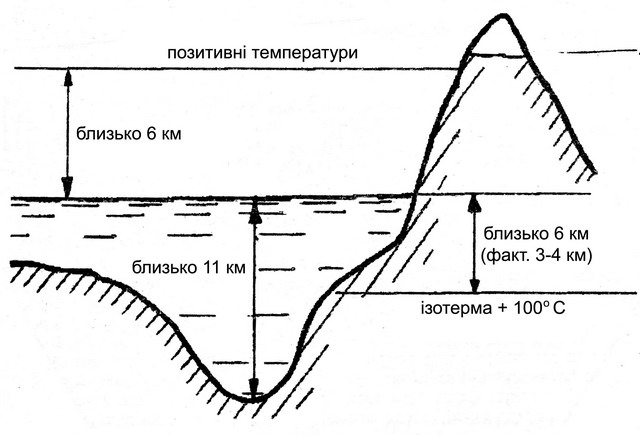
Межі поширення життя
Колообіг води

Колообіг вуглецю

Колообіг азоту

Определение: Число А называется пределом функции в точке х0, если для любой последовательности значений аргумента, сходящейся к точке х0,соответствующая последовательность значений функции сходится к числу А.
Методы вычисления пределов:
1. По теоремам о пределах.
Теорема 1. Любая функция имеет единственный предел в точке.
Теорема 2. Предел суммы (разности) функций равен сумме (разности) пределов данных функций.
Теорема 3. Предел произведения функций равен произведению пределов данных функций.
Теорема 4. Предел частного функций равен частному пределов данных функций, если предел знаменателя не равен нулю.
2. Если предел знаменателя равен нулю, то применяются методы разложения на множители:
- разложение квадратного трехчлена на множители;
- вынесение общего множителя за скобку;
- метод группировки;
- формулы сокращенного умножения.
3. При раскрытии неопределенности  используется:
используется:
- первый замечательный предел
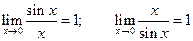
- второй замечательный предел
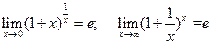
4. Предел функции при 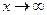 .
.
- Функция называется бесконечно-малой, если ее предел равен нулю.
- Функция называется бесконечно-большой, если ее предел равен бесконечности.
- Функция, обратная бесконечно-большой является бесконечно-малой; функция, обратная бесконечно-малой является бесконечно-большой.
5. Таблицаэквивалентностей:
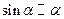
| 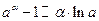
|
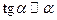
| 
|
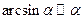
| 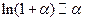
|
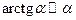
| 
|
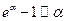
| 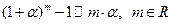
|
6. Правило Лопиталя.
Если f(x) и g(x) дифференцируемые в окрестности точки х0 функции и 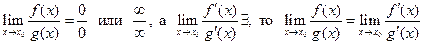
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1324; Нарушение авторских прав?; Мы поможем в написании вашей работы!