Определение деформаций и напряжений при растяжении-сжатии

Допущения, принимаемые при расчетах на прочность

Из-за сложности расчетов звеньев на прочность принимаются некоторые упрощающие расчет допущения относительно свойств материалов и характера взаимодействия звеньев и нагрузок. Экспериментальная проверка расчетных зависимостей, полученных с учетом принимаемых допущений, показала возможность их использования для практических расчетов.

Детали механизмов перестают выполнять свои функции не только при разрушении, но и при изменении своих размеров, формы, т.е. приобретая заметные остаточные деформации. Поэтому определение напряжений и деформаций проводят в области упругих деформаций, считая, что материал деталей обладает способностью полностью восстанавливать первоначальные форму и размеры тела после устранения причин, вызвавших его деформацию, т. е. обладает свойством идеальной упругости.

– Материал деталей является однородным и сплошным, т. е. свойства материала не зависят от размера и формы детали и одинаковы во всех ее точках, будь это композиционный материал, пластмасса или сплав.

– Материал детали изотропен, т.е. обладает во всех направлениях одинаковыми свойствами. Различие свойств в разных направлениях (анизотропия) учитывают при расчете деревянных деталей.

– В теле до приложения нагрузки нет начальных внутренних сил, т. е. отсутствуют напряжения.

– Деформации тела очень малы по сравнению с его размерами и не оказывают влияния на взаимное расположение нагрузок.

– Деформации материала в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).

– Принцип независимости действия сил (принцип наложения) – результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу отдельно в любом порядке.

– Принцип Сен-Венана – в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил мало зависит от конкретного способа приложения этих нагрузок. Этот принцип позволяет замену одной системы сил другой более простой системой, статически эквивалентной первой, что упрощает расчет, например, замену системы распределенных сил равнодействующей, приложенной в центре масс.

– Гипотеза плоских сечений (гипотеза Бернулли) – поперечные сечения стержней, плоские до приложения нагрузки, остаются плоскими и нормальными к продольной оси стержня при действии нагрузки.

Возьмем стержень (см. рис. 5.3, а), длиной ℓ, шириной b и нанесем на его поверхность координатную сетку, т. е. линии вдоль и перпендикулярно продольной оси. К торцам стержня приложим силы, направленные вдоль продольной оси. Стержень испытывает деформацию растяжения, длина его увеличилась на величину

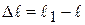, (5.3)

а ширина уменьшилась на величину

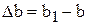, (5.4)

где ℓ₁, b₁ – соответственно длина и ширина стержня после приложения сил. Величины Δℓ и Δb называют абсолютным удлинением и сужением стержня или абсолютной продольной и поперечной деформацией. Величину

ε = Δℓ/ ℓ (5.5)

называют относительной линейной деформацией или относительным удлинением.

Соответственно ε₁ = Δb/ b называется относительной поперечной деформацией. Абсолютная величина отношения относительной поперечной деформации ε₁ к относительной продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона

μ = | ε₁/ ε |, (5.6)

который характеризует упругие свойства материала, его способность к поперечным деформациям. Величина коэффициента Пуассона определяется экспериментально и для различных материалов колеблется в пределах от нуля (для пробки), приближаясь к значению 0,5 (для резины). Для большинства металлических сплавов коэффициент Пуассона находится в пределах от 0,23 до 0,36 (для стали μ = 0,25 … 0,33; для чугуна μ = 0,23 … 0,27; для медных сплавов μ = 0,31 … 0,36; для алюминиевых сплавов μ = 0,32 … 0,36).

Замечено, что прямые линии, перпендикулярные продольной оси стержня, остаются прямыми и после деформаций, т.е. подтверждается гипотеза плоских сечений (гипотеза Бернулли). Это позволяет утверждать, что деформации (удлинения) и, в соответствии с законом Гука, напряжения образующих стержня, параллельных оси, в любом поперечном сечении равны, т.е. деформации и напряжения во всех точках поперечного сечения одинаковы.

Определим внутренние силы в поперечном сечении (см. рис. 5.3, б), воспользовавшись методом сечений. Они уравновешивают внешнюю силу F, складываясь в равнодействующую внутренних сил N. Из уравнения равновесия в проекциях сил на продольную ось стержня определим, что N = F.

Составляющая внутренних сил N направлена по нормали к поперечному сечению, поэтому в сечении действуют нормальные напряжения, величина которых определяется с учетом равномерного распределения их по сечению как

σ = N /A = F/ A, (5.7)

где А * – площадь поперечного сечения стержня.

При упругих деформациях справедлив закон Гука, устанавливающий линейную зависимость между напряжением и деформацией,

σ = E·ε. (5.8)

Коэффициент пропорциональности Е называют модулем упругости материала (модулем Юнга). Он является физической постоянной материала, характеризует, как и коэффициент Пуассона, его упругие свойства и определяется опытным путем.

Подставив в выражение (5.8) значения σ (5.7) и ε (5.5), получим формулу для определения абсолютного удлинения стержня

Δℓ = (N·ℓ)/ (E·A). (5.9)

Произведение Е·А характеризует сопротивляемость стержня к удлинению (сжатию) и называется жесткостью стержня при растяжении (сжатии).

Формулой (5.9) можно пользоваться для определения абсолютной продольной деформации стержня длиной ℓ при условии, что площадь сечения стержня в пределах всей длины постоянна и продольная сила N во всех поперечных сечениях одинакова. Если параметры E, N, A по длине не постоянны, формула (5.9) позволяет определить удлинение только отдельного i–го участка стержня, а его полное удлинение определяется как алгебраическая сумма изменений длин участков

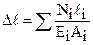. (5.10)

При этом границами характерных участков являются точки приложения внешних продольных сил F_i; места изменения поперечных размеров (A_i) и границы соединения растягиваемого элемента (E_i) из разных материалов. Продольная сила N_i на i-ом участке равна алгебраической сумме проекций на продольную ось стержня сил, действующих по одну (любую) сторону от сечения.

Сжатие отличается от растяжения только направлением внешних сил. Принято считать внешние продольные силы, напряжения и деформации при растяжении положительными, а при сжатии – отрицательными. Зависимости по определению деформаций и напряжений при растяжении имеют место и при сжатии, но при сжатии длина стержня уменьшается, а поперечные размеры увеличиваются.

Пример. Определить внутренние силы и напряжения в поперечных сечениях участков с длиной ℓ₁, ℓ₂, ℓ₃, а также перемещения точек приложения внешних продольных сил F₁, F₂ и F₃ ступенчатого стержня (рис. 5.7). Модули упругости материала участков E₁, E₂, E₃ и величины поперечных сечений постоянны по длинам участков и равны соответственно A₁, A₂, A₃.

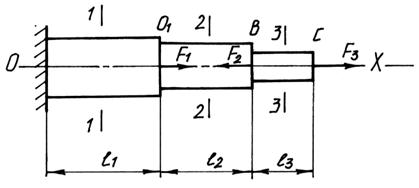
Рис. 5.7

Пользуясь методом сечений (подразд. 5.1), определим внутренние продольные силы в сечениях 1–1, 2–2 и 3–3. Так как силы реакции в месте закрепления (торец 0) стержня неизвестны, составляем для определения внутренних сил уравнения равновесия известных сил, т.е. сил, действующих на стержень справа от рассматриваемых сечений. Проектируя внешние и внутренние силы на продольную ось стержня, имеем

N_1–1 = F₁ – F₂ + F₃; N_2–2 = – F₂ + F₃; N_3–3 = F₃ .

Напряжения в поперечных сечениях участков OO₁,O₁B и BC соответственно равны σ₁ = N_1–1/A₁; σ₂ = N_2–2/A₂; σ₃ = N_3–3/A₃.

Определим изменения длин участков ℓ₁, ℓ₂, ℓ₃ стержня

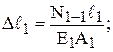
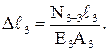
Перемещение Δℓ точки О равно нулю, точки приложения сил: F₁: = Δℓ₁; F₂: Δℓ_B = Δℓ₁ + Δℓ₂; F₃: Δℓ_C = Δℓ₁ + Δℓ₂ + Δℓ₃.

Силы веса стержня в данном примере не участвовали. Если при заданных схемах нагружения стержней их силы веса способствуют деформации растяжения (сжатия), то их нужно учитывать с соответствующим знаком при определении продольных внутренних сил N, напряжений и деформаций стержня.

Дата добавления: 2014-11-29