Материалы для подготовки к работе

Исследование разветвленной цепи переменного тока с индуктивным и емкостным сопротивлениями

ЛАБОРАТОРНАЯ РАБОТА № 4

Контрольные вопросы

1. В чем заключается явление резонанса напряжений и при каких условиях оно возникает?

2. Какую опасность представляет резонанс напряжений для электротехнических устройств?

3. Изменением каких параметров электрической цепи можно получить резонанс напряжений?

4. Как практически определить резонанс напряжений?

5. Запишите выражения для тока, полного сопротивления и коэффициента мощности электрической цепи при резонансе напряжений.

Цель работы:

1. Экспериментальным путем получить резонанс токов.

2. Исследовать влияние изменения проводимости цепи на токи и проводимости разветвленной цепи с индуктивным и емкостным сопротивлениями.

В разветвленной цепи, состоящей из двух ветвей, одна из которых имеет активное сопротивление R и индуктивность L, а другая емкость C при условии, что индуктивная и емкостная проводимости ветвей равны между собой (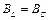) возникает особый режим работы, который называется резонансом токов.

Простейшей электрической цепью, в которой может наблю­даться резонанс токов, является цепь с параллельным соединени­ем катушки индуктивности и конденсатора (рис. 4.1).

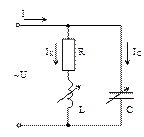
Рис. 4.1. Разветвленная цепь с R, L и C

Полная проводимость рассматриваемой цепи

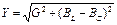
Условие резонанса токов (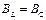) можно записать через соот­ветствующие параметры электрической цепи. Так как реактивная проводимость катушки определяется выражением 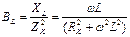, а проводи­мость конденсатора без учета его активного сопротивления (R_C =0) 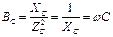, то условие резонанса может быть записано в виде .

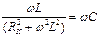Резонанс токов можно получить путем изменения одной из трех величин L, C или f при постоянных двух других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении ука­занных параметров.

Простейшие резонансные цепи, состоящие из параллельно со­единенных между собой катушки индуктивности и конденсатора, широко применяют в радиоэлектронике в качестве колебатель­ных контуров, в которых резонанс токов достигается при некото­рой определенной частоте поступающего на вход соответствую­щего устройства сигнала.

В лабораторных условиях наиболее часто резонанс токов достигается при неизменной емкости С конденсатора, путем изменения индуктивности L катушки. С изменением индуктивной проводимости 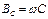, пропорциональной емкости кон­денсатора, происходит изменение полной проводимости Y, общего тока I и коэффициента мощности .

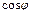Указанные зависимости называются резонансными кривыми (рис. 4.2).

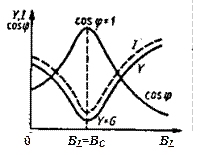
Рис. 4.2. Резонансные кривые

Резонанс токов ха­рактеризуется следующими явлениями:

1.В состоянии резонанса токов полная проводимость цепи равна активной проводимости 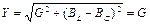и является наименьшей.

2.Минимальное значение проводимости обусловливает и минимальное значение тока цепи: I=YU=GU.

3.Индуктивная и емкостная составляющая токов в ветвях цепи равны между собой: .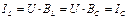

Ток в неразветвленной части цепи при этом имеет наименьшее значение и является чисто активным, т.е. совпадает по фазе с напряжением U, приложенным к зажимам цепи: .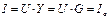

При этом реактивные составляющие тока I_L и I_C (в зависимо­сти от значения реактивных проводимостей) могут приобретать теоретически весьма большие значения и намного превышать ток I, потребляемый электрической цепью из сети.

4. Реактивная составляющая полной мощности, потребляемой цепью, при 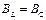оказывается равной нулю: Q=B_LU²-B_CU²=Q_L-Q_C= 0.

При этом индуктивная и емкостная составляющие реактив­ной мощности также могут приобретать весьма большие значе­ния, оставаясь равными друг другу.

5. Полная мощность цепи при резонансе равна ее активной составляющей: S=YU²=G U²=P.

6. Коэффициент мощности цепи:

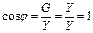, а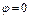

Векторная диаграмма разветвленной цепи с R, L и C при резонансе токов показана на рис. 4.3

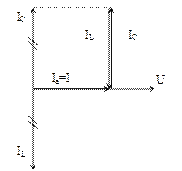
Рис. 4.3. Векторная диаграмма разветвленной цепи с R, L и С при резонансе токов

Если цепь не находится в резонансе, то она может работать в индуктивном () или емкостном (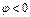) режиме (рис. 4.4)

а) б)

Рис. 4.4. Векторные диаграммы разветвленной цепи с R, L и C:

а – при преобладании индуктивной нагрузки;

б – при преобладании емкостной нагрузки

При выполнении лабораторной работы 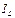рассчитывается по формуле

,

где - ток катушки.

, .

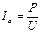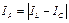Дата добавления: 2014-11-29