Материалы для подготовки к работе. Исследование неразветвленной цепи переменного тока с активным, индуктивным и емкостным сопротивлениями

Исследование неразветвленной цепи переменного тока с активным, индуктивным и емкостным сопротивлениями

ЛАБОРАТОРНАЯ РАБОТА № 3

Контрольные вопросы

1. Методика расчёта по методу наложения.

2. В каких случаях для расчёта сложной цепи целесообразно применять метод наложения?

3. Почему нельзя применять метод наложения для определения мощностей?

4. Сформулировать первый закон Кирхгофа.

5. Почему метод наложения не используется при анализе нелинейных цепей?

Цель работы:

1. Экспериментальным путем получить резонанс напряжений.

2. Исследовать влияние изменения индуктивности на ток и напряжения на участках неразветвленной цепи, содержащей R, L и C, а также на параметры цепи.

В неразветвленной цепи с активным сопротивлением R, индуктивностью L и емкостью C (рис. 3.1) при условии, что индуктивное и емкостное сопротивления равны между собой (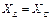), возникает особый режим работы, который называется резонансом напряжений.

Рис. 3.1. Неразветвленная цепь с R, L и C

Из условия резонанса напряжений ( или ) следует, что при заданных значениях индуктивности и емкости резонанс напряжений в цепи возникает при угловой частоте 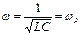или частоте 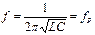, которые называют резонансными и обозначают соответственно и .

Резонансная частота определяется исключительно параметрами цепи и поэтому называется частотой собственных колебаний цепи. Таким образом, в неразветвленной цепи с R, L и C резонанс напряжений возникает в случае, когда частота вынужденных колебаний (частота приложенного напряжения) оказывается равной частоте собственных колебаний цепи.

Резонанс напряжений можно получить путем изменения одной из трех величин L, C или f при постоянных двух других.

В простейшем случае резонанс напряжений может быть полу­чен в электрической цепи переменного тока при последователь­ном включении катушки индуктивности и конденсаторов. При этом, изменяя индуктивность катушки при постоянных парамет­рах конденсатора, получают резонанс напряжений при неизменных значениях напряжения и емкости, частоты и активного со­противления цепи. При изменении индуктивности L катушки про­исходит изменение реактивного индуктивного сопротивления. При этом полное сопротивление цепи также изменяется, следователь­но, изменяются ток, коэффициент мощности, напряжения на ка­тушке индуктивности, конденсаторах и активном сопротивлении катушки и активная, реактивная и полная мощности электриче­ской цепи. Зависимости тока I, коэффициента мощности cosφ и полного сопротивления Z цепи переменного тока в функции индуктивного сопротивления (резонансные кривые) для рассматри­ваемой цепи приведены на рис. 3.2.

Рис. 3.2. Резонансные кривые

Резонанс напряжений характеризуется рядом су­щественных факторов.

1. При резонансе напряжений полное сопротивление электрической цепи переменного тока принимает минимальное значение и оказывается равным ее активному сопротивлению, т. е.

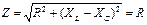, так как при этом X_L=X_C.

2. Из этого следует, что при неизменном напряжении питаю­щей сети (U=const) при резонансе напряжений ток в цепи достигает наибольшего значения 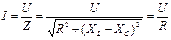и совпадает по фазе с напряжением U, приложенным к зажимам цепи. Теоретически ток может достигать больших значений, определяемых напряжением сети и активным сопротивлением катушки. При малом значении активного сопротивления ток может достигать большого значения.

3. Коэффициент мощности цепи равен единице т.е. принимает наибольшее значение, которому соответствует угол .

4. Активная мощность при резонансе P=RI² имеет наибольшее значение, равное полной мощности S, в то же время реактивная мощность цепи Q=XI²= (X_L-X_C) I² оказывается равной нулю: Q=Q_L-Q_C=0.

При этом реактивная индуктивная и реактивная емкостная составляющие полной мощности Q_L=Q_C=X_LI²=X_CI² могут при­обретать теоретически весьма большие значения, в зависимости от значений тока и реактивных сопротивлений.

5. При резонансе напряжений напряжения на емкости и ин­дуктивности оказываются равными 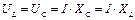и в зависи­мости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение пи­тающей сети. При этом напряжение на активном сопротивлении оказывается равным напряжению питающей сети, т. е. U_R=U.

Резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, так как может при­вести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденса­торов при возможном перенапряжении на отдельных участках цепи. В то же время резонанс напряжений в электрических цепях переменного тока широко используется в радиотехнике и элек­тронике в различного рода приборах и устройствах, основанных на резонансном явлении.

Векторная диаграмма неразветвленной цепи с R, L и C при резонансе напряжений показана на рис. 3.3.

Рис. 3.3. Векторная диаграмма неразветвленной цепи с R, L и С при резонансе напряжений

Если цепь не находится в резонансе, то она может работать в индуктивном () или емкостном () режиме (рис. 3.4).

а) б)

Рис. 3.4. Векторные диаграммы неразветвленной цепи с R, L и C:

а – при преобладании индуктивной нагрузки;

б – при преобладании емкостной нагрузки

При выполнении лабораторной работы напряжение на индуктивном сопротивлении катушки рассчитывается по формуле

,

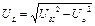где - напряжение, измеренное на катушке.

Вычисления производятся по следующим формулам:

, , .

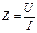Дата добавления: 2014-11-29