Контрольная работа 3 страница

Построения проекций промежуточных точек одинаковы для каждой точки. Чтобы построить проекции точки 1 сначала произвольно определяют ее положение на той плоскости проекций, которой перпендикулярна секущая плоскость (в рассматриваемом случае на П₂). Чтобы построить точку 1₁ мысленно проводят вспомогательную горизонтальную (параллельную плоскости проекций П₁) секущую плоскость через точку 1₂. В результате рассечения получается окружность радиуса R₁, определяемый на плоскости проекций П₂ (измеряют расстояние на уровне секущей плоскости от вертикальной оси до образующей). На плоскости проекций П₁ на линии связи, проведенной из точки 1₂,делают засечки измеренного радиуса из центра проекции сферы. Так строят проекции точки 1 (их всего две) на плоскости проекций П₁. На профильной плоскости проекций проводят линию связи из точки 1₂. Широту точки определяют на горизонтальной плоскости проекций как расстояние от горизонтальной оси до точки 1₁ и откладывают на профильной плоскости проекций от вертикальной осевой по линии связи. Так определяют положение профильных проекций точки 1 (их всего две).

При построении линии пересечения сферы с плоскостью необходимо определить видимость этой линии. На рисунке 10 изображены проекции линии пересечения с учетом видимости. На плоскости проекций П₂ линия пересечения – отрезок, который является видимым по всей длине. На плоскости проекций П₁ линия пересечения – эллипс, часть которого является невидимой. При определении видимости горизонтальной проекции линии пересечения смотрят на ее фронтальную проекцию сверху. Важно определить границу видимости. При рассмотрении сферы сверху видимыми будут все точки, принадлежащие верхней половине сферы, а на эпюре это будут точки, принадлежащие верхней половине фронтальной проекции сферы. Таким образом при определении видимости линии пересечения на горизонтальной

плоскости проекций границей видимости является точка b₂. Все точки, принадлежащие отрезку d₂b₂,являются видимыми, т.к. принадлежат части проекции линии пересечения, находящейся в верхней половине фронтальной проекции сферы. Точки, принадлежащие отрезку b₂а₂, будут невидимыми, следовательно, линия пересечения, проходящая через эти точки, будет невидимой При определении видимости профильной проекции линии пересечения смотрят на ее фронтальную проекцию слева. Границей видимости будет вертикальная осевая линия, делящая изображение на левую и правую половины. Видимыми на плоскости проекций П₃ будут все точки, принадлежащие левой половине сферы, а на эпюре это будут точки, принадлежащие левой половине фронтальной проекции сферы. Границей видимости для линии пересечения будет точка с₂, принадлежащая вертикальной осевой линии. Все точки, принадлежащие отрезку а₂с₂, являются видимыми, т.к. принадлежат части проекции линии пересечения, находящейся в левой половине фронтальной проекции сферы. Точки, принадлежащие отрезку с₂d₂, будут невидимыми, следовательно, линия пересечения, проходящая через эти точки, будет невидимой (невидимые контуры на чертеже обводят штриховой линией, обозначение невидимых точек заключают в скобки).

Рисунок 10 – Построение проекций линии пересечения сферы и плоскости

с учетом видимости

Р е ш е н и е. В правой части листа намечают оси координат. По заданным координатам определяют положение проекций точки О, центра сферы, и строят проекции сферы диаметром 100 мм. По координатам своего варианта строят фронтальную проекцию сквозного отверстия в сфере. Определяют и обозначают латинскими строчными буквами характерные точки линий сквозного отверстия: точки на экваторе, главном меридиане, наиболее удаленные и ближайшие точки поверхности сферы к плоскостям проекций, точки концов большой и малой осей эллипсов, точки касания кривых проекций очерков, точки, лежащие на границе видимости. Чтобы построения кривой линии были точнее, ее строят по ряду точек. Поэтому, кроме

характерных, выполняют построения промежуточных точек, которые обозначают арабскими цифрами. При обводке учитывают видимость линий.

Следы вспомогательных секущих плоскостей следует обозначить, линии построения (сплошные тонкие линии толщиной s / 3) – сохранить.

Лист 4. Задача 7 «Конус с вырезом (или окном)»

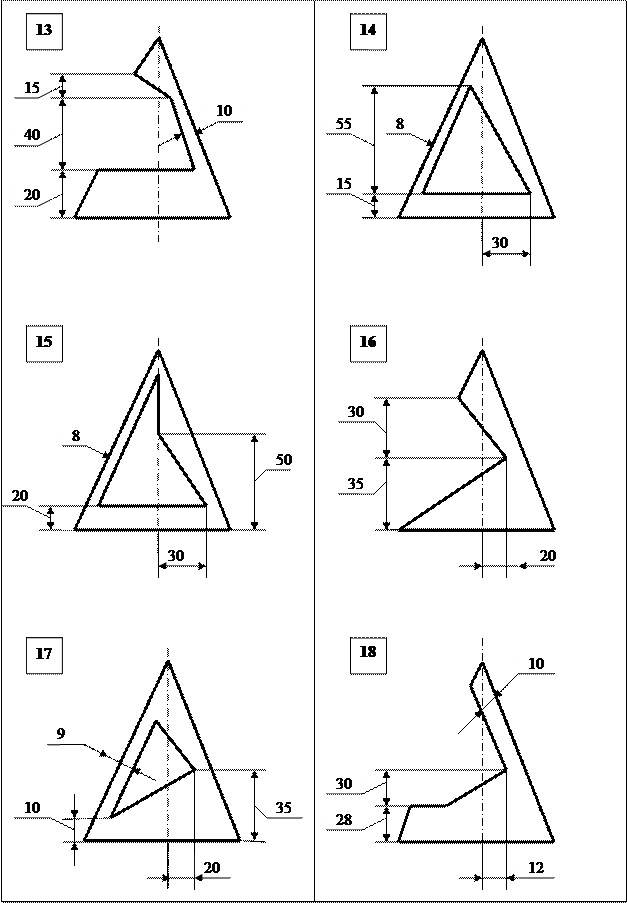
Задание. Построить круговой конус со сквозным поперечным вырезом (окном) призматической формы в трех проекциях. Диаметр основания конуса 90 мм, высота 100 мм. Данные к задаче 7 приведены в таблице 5 /3/. Компановка листа приведена на рисунке 11.

В начертательной геометрии поверхность рассматривают как множество последовательных положений движущейся линии или другой поверхности в пространстве. Линию (поверхность), перемещающуюся в пространстве и образующую поверхность, называют образующей. Образующие могут быть прямыми и кривыми.

Одна и та же поверхность в ряде случаев может рассматриваться как образованная движением различных образующих.

Образующие поверхность кривые могут быть постоянными и переменными, например закономерно изменяющимися. Образующая поверхности в процессе движения может изменять свою форму и геометрические размеры.

При изображении поверхности на чертеже показывают лишь некоторые из множества положений образующей.

Поверхности можно разбить на классы:

●линейчатые:

- линейчатые поверхности с одной направляющей (коническая, цилиндрическая, с ребром возврата, торс),

- линейчатые поверхности с двумя направляющими (цилиндроид, коноид,

гиперболический параболоид (косая плоскость)),

- линейчатые поверхности с тремя направляющими (однополостный гиперболоид);

● винтовые:

- прямая винтовая поверхность (винтовой коноид, прямой геликоид),

- косая винтовая поверхность (наклонный геликоид);

● циклические:

- каналовая поверхность,

- трубчатая поверхность;

● поверхности вращения:

- цилиндрическая,

- коническая,

- сфера,

- тор.

Поверхность вращения – поверхность, получающаяся при вращении некоторой образующей линии вокруг неподвижной прямой – оси поверхности. На чертежах ось изображают штрихпунктирной линией. Образующая может иметь как кривые, так и прямолинейные участки. Поверхность вращения на чертеже задается образующей и положением оси. При вращении каждая точка образующей описывает окружность в плоскости, перпендикулярной оси. Следовательно, линия пересечения поверхности вращения любой плоскостью, перпендикулярной оси, является окружностью. Такие окружности называются параллелями. Параллель, проходящая через наиболее удаленную от оси точку, называется экватором, через самую близкую точку – горлом. Линия пересечения поверхности вращения

плоскостью, проходящей через ось вращения, называется меридианом. Меридиан, лежащий в

плоскости, параллельной П₂, называется главным.

		Задача 7		Задача 8
	Рисунок 11 – Компановка листа 4

Продолжение таблицы 5

Продолжение таблицы 5

Продолжение таблицы 5

Цилиндрическая поверхность образуется вращением прямой (образующей) относительно неподвижной оси, параллельной образующей.

Если цилиндрическую поверхность ограничить двумя плоскостями, то получится круговой цилиндр. Такие плоскости называют основаниями цилиндра. Круговой цилиндр может быть прямой и наклонный. Прямым называют цилиндр, у которого основание перпендикулярно оси вращения. Если поверхность прямого кругового цилиндра на одну из плоскостей проекций проецируется в линию – окружность (когда основание цилиндра параллельно одной из плоскостей проекций), то такую поверхность называют проецирующей. Меридиан прямого кругового цилиндра – прямоугольник). При ортогональном проецировании проекции прямого кругового цилиндра на двух плоскостях проекций – равные прямоугольники(высота равна высоте цилиндра, длина равна диаметру основания цилиндра), на третьей – окружность (диаметр равен диаметру основания конуса).

Коническая поверхность образуется вращением прямой (образующей), закрепленной в некоторой точке на неподвижной оси вращения вокруг этой оси.

Если такую поверхность ограничить плоскостью, перпендикулярной оси, то получится прямой круговой конус. Меридиан прямого кругового конуса – равнобедренный треугольник.). При ортогональном проецировании проекции прямого кругового конуса на двух плоскостях проекций – равные равнобедренные треугольники (высота равна высоте конуса, длина основания равна диаметру основания конуса), на третьей – окружность (диаметр равен диаметру основания конуса).

Сфера – ограниченная поверхность вращения. Она образуется вращением окружности (образующей) вокруг неподвижной оси, проходящей через центр окружности. Экватор и меридианы сферы – равные между собой окружности (их диаметр равен диаметру сферы). При ортогональном проецировании на все плоскости проекций сфера проецируется в окружности равного диаметра.

Тор – поверхность, образующаяся при вращении окружности (или ее дуги) вокруг неподвижной оси, лежащей в плоскости окружности, но не проходящей через ее центр. Если ось вращения проходит через образующую-окружность, тор получается самопересекающийся, если касательно к ней – закрытый, если ось вращения находится вне образующей-окружности – открытый (круговое кольцо).

Р е ш е н и е. Круговой конус – поверхность второго порядка. Плоскость, не проходящая через его вершину, пересекает конус по окружности, эллипсу или параболе, если она расположена по одну сторону от вершины, и по гиперболе, если она пересекает его по обе стороны от вершины.

Если секущая плоскость проходит через вершину конуса, то линия пересечения - треугольник. На рисунке 12 изображены проекции линии пересечения с учетом видимости прямого кругового конуса с плоскостью А, проходящей через его вершину.

Рисунок 12 – Построение проекций линии пересечения кругового конуса и

проецирующей плоскости, проходящей через вершину

Если секущая плоскость параллельна основанию, то линия пересечения с прямым круговым конусом – окружность. На рисунке 13 изображены проекции линии пересечения с учетом видимости прямого кругового конуса с плоскостью А, перпендикулярной оси.

В остальных случаях линией пересечения является кривая линия, построение проекций которой выполняют методом секущих плоскостей по ряду точек. Секущие плоскости являются проецирующими и параллельными основанию конуса. Сначала определяют проекции характерных точек, которые обозначают строчными латинскими буквами (а, b, c), а затем промежуточных, которые обозначают арабскими цифрами.

Точки кривой линии произвольно выбирают на проекции линии пересечения на той плоскости проекций, которой перпендикулярна секущая плоскость (в рассматриваемом случае на П₂), т.к. на нее кривая проецируется в отрезок. Они будут принадлежать фронтальной проекции линии пересечения секущей плоскости и кругового конуса.

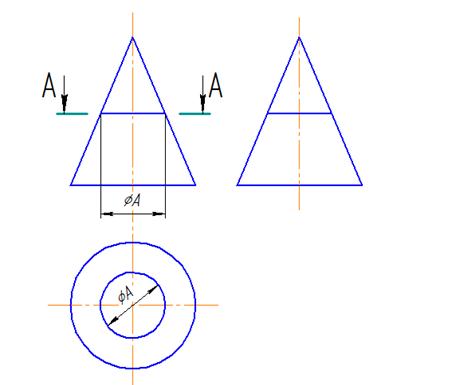
Рисунок 13 – Построение проекций линии пересечения кругового конуса и

плоскости, перпендикулярной оси

Рисунок 14 – Положение секущей плоскости относительно

вершины конической поверхности:

а) по одну сторону от вершины

б) по обе стороны от вершины

Пример построения проекций промежуточной точки 1 приведен на рисунке 15. На фронтальной проекции линии пересечения секущей плоскости А и прямого кругового конуса

определяют положение промежуточной точки 1. Через нее мысленно проводят вспомогательную секущую плоскость Р (фронтально-проецирующую), параллельную основанию конуса. На чертеже положение секущей плоскости обозначено Р₂1. Эта плоскость рассечет конус по окружности, радиус которой определяют как расстояние от осевой линии конуса до образующей – R1. Точка 1 принадлежит данной окружности. Поэтому для определения горизонтальной проекции точки на плоскости проекций П₁ строят окружность (дугу) радиуса R1 и на нее проецируют точку 1. Поскольку горизонтальная проекция линии пересечения симметрична относительно горизонтальной оси, то проекцию точки 1₁' строят симметрично проекции точки 1₁. Третью проекцию точек строят по двум известным.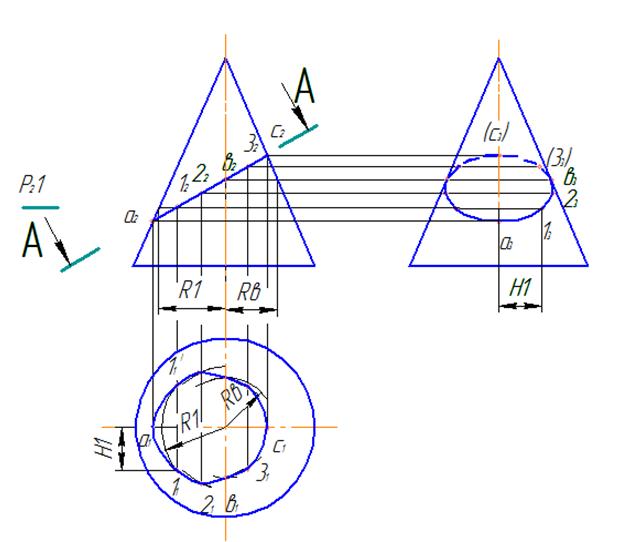

Рисунок 15 – Построение эллипса

Если секущая плоскость, расположена по одну сторону от вершины конической поверхности и пересекает две образующие прямого кругового конуса, линия пересечения – эллипс. Пример такого расположения секущей плоскости приведен на рисунке 14, а. Пример построения эллипса приведен на рисунке 15.

Построения начинают с определения проекций характерных точек. Точки а₂ и с₂ являются точками пересечения проекции секущей плоскости Р₂ и образующими конуса. На горизонтальную плоскость проекций эти образующие проецируются в горизонтальную осевую

линию, следовательно точки а₁ и с₁ будут принадлежать этой осевой. На профильную плоскость проекций данные образующие проецируются в вертикальную осевую линию, следовательно точки а₃ и с₃ будут принадлежать данной осевой. Точка b₂ является точкой пересечения проекции секущей плоскости Р₂ и осевой конуса. Горизонтальные проекции точки

b определяют методом секущих плоскостей. Профильные проекции этой точкибудут расположены на проекциях образующих.

Затем берут ряд промежуточных точек (более точное построение проекций линии пересечения обеспечивается построением проекций большего числа точек). Проекции промежуточных точек строят методом секущих плоскостей.

Далее определяют видимость проекций линии пересечения. Если рассматривать конус в положении, при котором его основание параллельно горизонтальной плоскости проекций, то боковая поверхность конуса на П ₁ полностью видна, следовательно горизонтальная проекция линии пересечения, принадлежащая поверхности конуса будет видимой. Видимость на фронтальной плоскости проекций определяют, глядя на горизонтальную снизу. Точки, а следовательно и линия, находящиеся на ближней по направлению взгляда половине изображения конуса будут видимыми. Другими словами, все геометрические элементы, находящиеся до осевой линии по направлению взгляда будут видимыми. А точки а ₁ и с₁ являются границей видимости. Определяя видимость на П₃, смотрят на фронтальную проекцию слева. Все геометрические элементы, находящиеся на ближней по направлению взгляда половине поверхности конуса, будут видимыми. Границей видимости является точка b₂, принадлежащая осевой линии. Невидимые контуры линии пересечения на чертеже обводят штриховой линией, обозначение невидимых точек заключают в скобки.

Если секущая плоскость, расположена по одну сторону от вершины конической поверхности и пересекает одну образующую прямого кругового конуса, линия пересечения – парабола. Пример построения параболы приведен на рисунке 16.

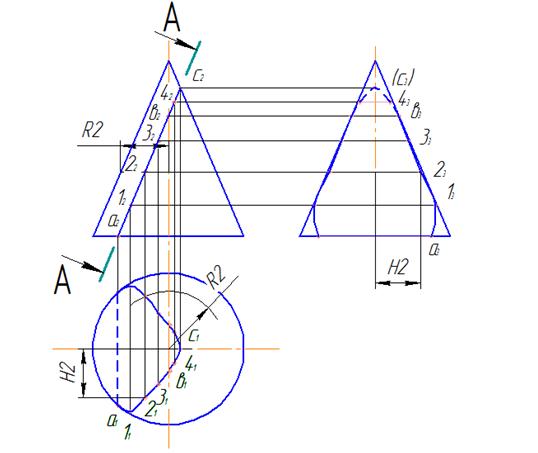
Рисунок 16 – Построение параболы

Если секущая плоскость, расположена по обе стороны от вершины конической поверхности и пересекает образующие прямого кругового конуса, линия пересечения – гипербола. Пример такого расположения секущей плоскости приведен на рисунке 14, б. Проекции точек гиперболы строят методом секущих плоскостей (смотри описание построения проекций эллипса). Видимость определяют по тем же правилам.

Приступая к решению задачи, в левой части листа намечают осевые линии. По заданным размерам чертят три проекции прямого кругового конуса и по заданию своего варианта фронтальную проекцию сквозного выреза (окна). Далее анализируют положение секущих плоскостей, определяющих форму выреза с целью определения вида линий, получающихся при пересечении конуса с этими плоскостями. Определяют и обозначают латинскими строчными буквами характерные точки линий сквозного отверстия: точки концов большой и малой осей эллипсов, точки касания кривых проекций очерков, точки, лежащие на границе видимости. Чтобы построения проекций кривой линии были точнее, ее строят по ряду точек. Поэтому, кроме характерных, выполняют построения промежуточных точек, которые обозначают арабскими цифрами. При обводке проекций линии выреза (окна) воспользуйтесь лекалом. Обводку производите с учетом видимости линий.

Следы вспомогательных секущих плоскостей следует обозначить, линии построения (сплошные тонкие линии толщиной s / 3) – сохранить.

Задача 8 «Пересечение поверхностей»

Задание. Построить линию пересечения заданных непрозрачных поверхностей (геометрических тел). Данные к задаче 8 приведены в таблице 6 /3/.

Для построения проекций лини пересечения поверхностей вращения часто используют метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей выбирают проецирующие плоскости, перпендикулярные осям тел вращения. Тела вращения на чертеже располагают так, чтобы их основания были параллельны одной из плоскостей проекций. Предложенные варианты заданий содержат два типа задач.

● О дна из поверхностей является проецирующей, т.е. на одну из плоскостей проекций проецируется в линию. К проецирующим относится прямой круговой цилиндр, т.к. его боковая поверхность перпендикулярна основанию и проецируется на одну из плоскостей проекций в окружность. В этом случае одна проекция линии пересечения поверхностей уже построена, и ее изображение совпадает с проекцией цилиндра. Пример решения такой задачи приведен на рисунке 17.

Пусть заданы пересекающиеся поверхности прямого кругового цилиндра и полусферы. Боковая поверхность цилиндра спроецировалась в линию (окружность) на плоскость проекций П₁. Так горизонтальная проекция линии пересечения совпала с горизонтальной проекцией цилиндра. Задача сводится к построению фронтальной проекции линии пересечения. На известной (горизонтальной) проекции линии пересечения определяют положение характерных точек: а и b лежат на основании полусферы, с принадлежит образующей цилиндра, d – образующей конуса (образующие цилиндра и конуса на плоскость проекций П₁ спроецировались в горизонтальную осевую линию).Затем между характерными точками на горизонтальной проекции линии пересечения берут ряд промежуточных точек (для более точного построения проекций линии пересечения берут большее количество точек). Определилась горизонтальная проекция линии пересечения а₁1₁2₁с₁d₁… b₁. Каждая из точек этой линии принадлежит как поверхности цилиндра, так и поверхности полусферы. Фронтальные проекции точек строят, рассматривая точки как принадлежащие полусфере. Пример построения фронтальных проекций точек приведен на рисунке 17, а. Сначала определяют окружность поверхности полусферы, которой принадлежит точка. Затем проецируют эту окружность на плоскость проекций П₂ – получают отрезок, параллельный

проекции основания полусферы. На этот отрезок проецируют точку поверхности сферы. Если одна из пересекающихся поверхностей сфера или часть сферы, то фронтальные проекции точек можно построить другим способом. Пример построения линии пересечения приведен на рисунке 17, б. Через каждую точку мысленно проводят вспомогательную секущую плоскость F, параллельную плоскости проекций П₂. Линия пересечения полусферы с секущей плоскостью F проецируется на плоскость проекций П₁ в часть окружности, на которую затем проецируют точку. На рисунке 18 приведен пример построения проекций промежуточных точек линии пересечения.

● Оси пересекающихся поверхностей вращения параллельны, т.е. поверхности являются соосными. Пример решения такой задачи приведен на рисунке 18. При построении линии пересечения двух соосных конусов, большого (с вершиной S и диаметром D) и малого (с вершиной s и диаметром d), вспомогательные секущие плоскости вводят перпендикулярно осям конусов. Секущие плоскости должны быть проецирующими. В результате рассечения обеих поверхностей введенной секущей плоскостью получают линию пересечения, которая на

плоскость проекций П₂ проецируется в отрезок, а на плоскость проекций П₁ – в окружности радиусами R (большого конуса) и r (малого конуса). Точки пересечения окружностей,

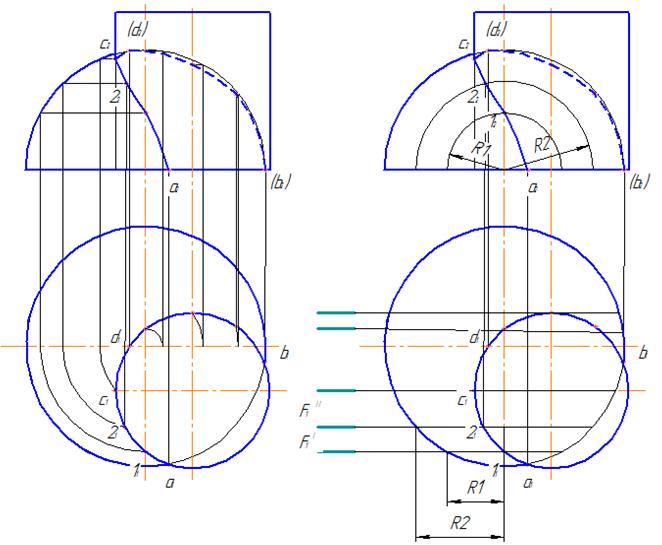
Рисунок 17 – Построение проекций линии пересечения

цилиндра и полусферы

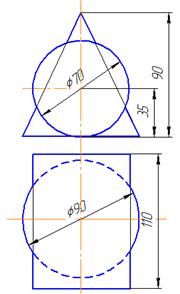
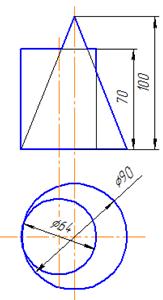
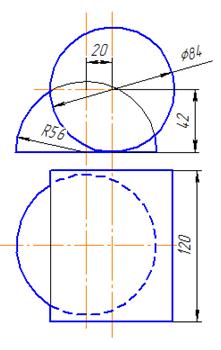
Таблица 6 – Данные к задаче 8

Продолжение таблицы 6

.

Продолжение таблицы 6

б

а

Дата добавления: 2014-11-29