Расчет выбега электродвигателей

Индивидуальный выбег при наличии близкого КЗ, что имеет место для расчетного случая, происходит по более крутой характеристике, чем при свободном выбеге так как двига­тель переходит в генераторный режим. В асинхронном двигателе, вследствие быстрого затухания эдс, тормозной момент практически не вызывает дополнительного торможения и в расчетах, как правило, не учитываются.

Таким образом, расчет индивидуального выбега без учета электромагнитных переходных процессов связан с решением дифференциаль­ного уравнения движения, которое может быть записано в виде:

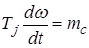; (4.4)

или . (4.5)

Ввиду гладкости функции для решения уравнения (4.14) могут быть использованы простые методы численного интегрирования дифференциальных уравнений, например, метод Эйлера [5]. Конечной целью расчета выбега является построение кривых выбега и нахождение скорости элек­тродвигателей к моменту восстановления питания.

При 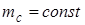можно получить кривую выбега в виде:

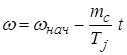, (4.6)

где - начальная частота вращения.

Практически, если время перерыва питания или КЗ меньше 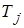в пять и более раз, можно пользоваться формулой (4.6) независимо от харак­тера момента сопротивления механизма.

При численном решении методом Эйлера алгоритм решения строится на последовательности временных интервалов . Так при решении урав­нения (4.5) находится приращение скольжения 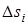на каждом ин­тервале:

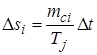, (4.7)

где 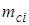находится по формуле (3.13) искольжение в начале следующего интервала находится как:

. (4.8)

Алгоритм расчета индивидуального выбега представлен в примере 3.

При групповом выбеге расчет зависимости частоты вращения от времени без учета электромагнитных переходных процессов может быть получен эквивалентированием двигательной нагрузки, основанной на двух допу­щениях:

– алгебраическая сумма мощностей, перераспределяемых между отдельны­ми двигателями при их групповом выбеге равна нулю;

– скорость изменения частоты вращения всех двигателей одинакова.

С учетом этих допущений синхронная частота вращения на секции в процессе выбега определяется как средневзвешенная скорость [1]:

, (4.9)

где - частота вращения i-го двигателя в момент времени t при индивидуальном выбеге; n - число двигателей, участвующих в групповом выбеге.

Использование формулы (4.9) предполагает расчет индивидуального выбега по изложенным ранее алгоритмам и последующее эквивалентирование их для заданного времени перерыва электроснабжения или работы на удаленное КЗ. Рассмотрение группового выбега при работе на КЗ имеет смысл только при достаточно большом внешнем сопротивлении. При КЗ на питающей секции шин точка КЗ разделяет двигатели, и выбег стано­вится индивидуальным.

Погрешность расчета по выражению (4.9) возрастает с увеличением разброса постоянных инерции .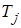

В том случае, когда выбегают электродвигатели с одинаковым харак­тером механических характеристик, можно свести задачу к решению одного уравнения движения с эквивалентной постоянной инерции:

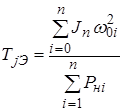. (4.10)

Решение уравнения движения проводится при этом для характерного двигателя группы.

Следует отметить приближенность рассмотренных, алгоритмов группово­го выбега. Более точно можно решить эту задачу лишь с учетом электро­магнитных переходных процессов, где вопросы обмета энергией решаются автоматически.

Дата добавления: 2014-11-29