Лінійного програмування. Використання EXCEL для розв’язання задач

Використання EXCEL для розв’язання задач

Задачі лінійного програмування можна розв’язувати за допомогою програми«Поиск Решения», яка входить у надбудови EXCEL пакета Microsoft Office.

1. Осуществляем ввод даних в таблицу Excel (рис. 1).

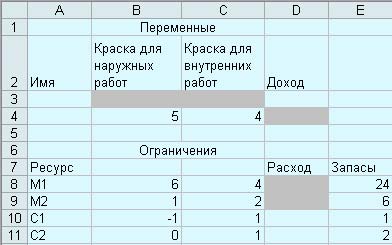
Рис. 1. Заполнение листа для решения задачи

Для змінних задачи x₁ и x₂ отведены ячейки B3 (имя ячейки - int) и C3 (имя ячейки - ext). Эти ячейки называются рабочими или изменяемыми ячейками. В изменяемые ячейки значения не заносятся и в результате решения задачи в этих ячейках будет отражено оптимальное значение переменной.

В ячейку D4 (имя ячейки - sum) вводится формула для вычисления целевой функции задачи (дохода) z = 5x₁+ 4x₂. Для этого необходимо выполнить следующие действия:

• поместить курсор в D4;
• вызвать Мастер функций;
• в появившемся окне выбрать "Математические" и "СУММПРОИЗВ" (рис. 2).

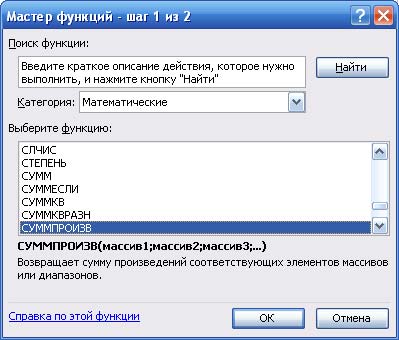
Рис. 2. Мастер функций, Шаг 1

В окне мастера функций нажать OK, в появившемся окне (рис. 3) в поле "массив 1" ввести (протаскивая курсор мыши по ячейкам) адреса

изменяемых ячеек B3:C3. В поле "массив 2" вводятся адреса ячеек содер-жащих цены на краски B4:C4, после нажать OK.

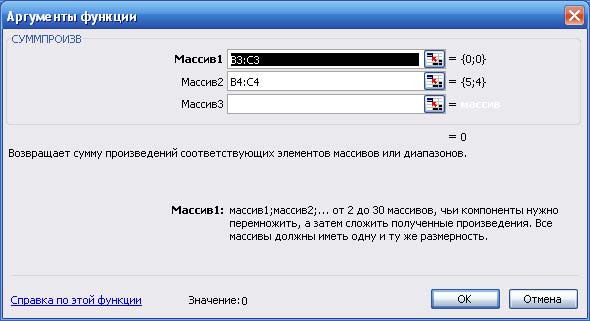
Рис. 3. Мастер функций, Шаг 2

В ячейку D8 вводится формула для вычисления израсходованного количества сырья M1: 6x₁+ 4x₂, а в ячейку D9 вводится формула для израсходованного количества сырья M2: x₁+ 2x₂. В ячейку D10 вводится формула для вычисления спроса на краску:- 1x₁+ 4x₂, а в ячейку D11 вводится формула ограничения на краску для внутренних работ: x₂. Эти формулы вводятся аналогично целевой функции.

В результате страница примет вид:

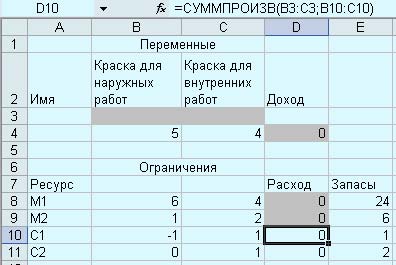
Рис. 4. Вид страницы после добавления формул

2. В меню "Сервис" выбираем процедуру "Поиск решения". В появившемся окне (рис. 5) нужно установить адрес целевой ячейки D4, значение целевой ячейки: максимальное, адреса изменяемых ячеек B3:C3.

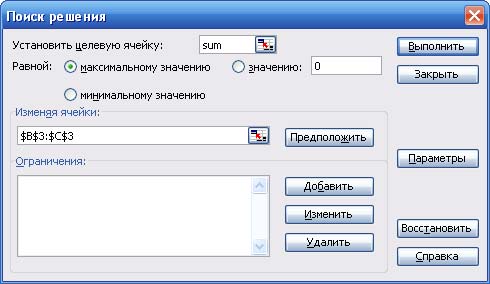
Рис. 5. Поиск решения

3. Чтобы ввести ограничения задачи, нажать кнопку "Добавить". В появившемся диалоговом окне слева ввести адрес D8 (израсходованное количество сырья M1), затем выбрать знак ≤ и в правой части количество сырья M2, равное 24 (или адрес ячейки E8). После ввода нажать кнопку "Добавить" и аналогично ввести второе ограничение.

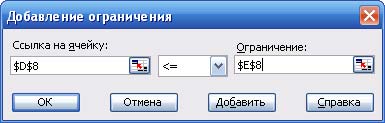
Рис. 6. Добавление ограничения

4. После ввода ограничений получим следующий вид окна поиска решения:

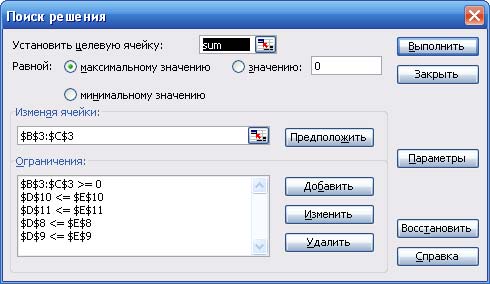
Рис. 7. Результат добавления ограничений

5. В окне "Поиск решения" нажать "Параметры" и в появившемся окне (рис. 8) установить флажок в пункте "Линейная модель". В этом случае при решении задачи будет использоваться симплекс - метод. Остальные значения можно оставить без изменения. После нажать кнопку ОК.

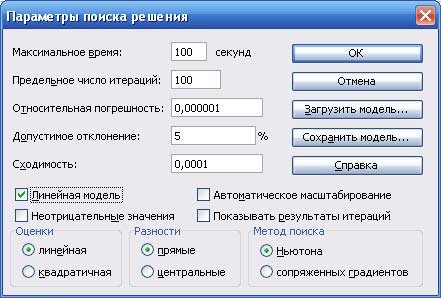
Рис. 7. Результат добавления ограничений

5. В окне "Поиск решения" нажать "Параметры" в появившемся окне (рис. 8) установить флажок в пункте "Линейная модель". В этом случае при решении задачи будет использоваться симплекс - метод. Остальные значения можно оставить без изменения. После нажать кнопку ОК.

Рис. 8. Окно Параметры

6. Для решения задачи в окне "Поиск решения" нажать кнопку "Выполнить". Если решение найдено появляется окно (рис. 9).

Рис. 9. Результаты поиска решения

7. Для просмотра результатов выбираем тип отчета: "Результаты" и нажимаем кнопку ОК. "Отчет по результатам" состоит из трех таблиц (рис. 10):

• в таблице 1 приводятся сведения о целевой функции;
• в таблице 2 приводятся значения переменных задачи;
• в таблице 3 показаны результаты поиска для ограничений задачи.

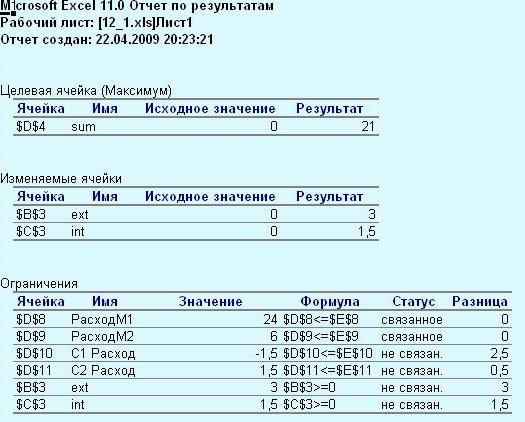
Рис. 10. Отчет Результаты

Из этих таблиц видно, что в оптимальном решении:

производство краски для наружных работ B3 = 3;

производство краски для наружных работ B3 = 3;

производство краски для внутренних работ С3 = 1.5;

при этом доход D4 = 21;

расход сырья М1 D8 = 24;

расход сырья М2 D9 = 6.

Таким образом, оба ресурса дефицитные (соответствующие

ограничения называются связанными).

Первоначальная таблица EXCEL заполняется результатами, отриману прі рішенні (рис. 11).

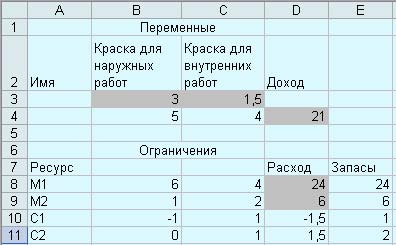
Рис. 11. Результат поиска решения

Додаток В

Дата добавления: 2014-11-29