Невласні інтеграли першого роду

Лекція № 30

Завдання для самостійної роботи

Розв’язання

Розв’язання

Використаємо формулу (29.11), для цього знайдемо:

,

.

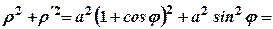
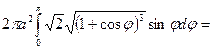
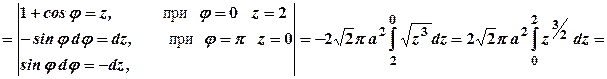
кв.од.

9. Обчислити площу поверхні тіла, утвореного обертанням лемніскати навколо полярної осі.

Обчислимо половину шуканої площі поверхні, а саме:

. Знайдемо з рівняння .

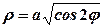Тоді .

Обчислимо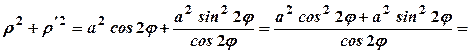

.

Тоді

.

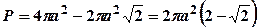кв. од.

Обчислити площі поверхонь тіл, утворених обертанням кривих навколо відповідної осі:

1. , , ?

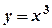2. , , ?

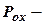3. , , ?

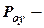4. , , ?

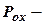5. Знайти поверхню сфери, заданої в полярних координатах.

§ 3. (С. р. Знаходження статичних моментів і координат центра мас. Теореми Гульдіна. Обчислення роботи та сили тиску.)

Тема: Невласні інтеграли першого роду. Невласні інтеграли другого роду.

План лекції:

§1. Невласні інтеграли першого роду.

§2. Невласні інтеграли другого роду

1. Невласні інтеграли першого роду – це інтеграли із нескінченним проміжком інтегрування.

Нехай f (x) інтегровна для будь-якого скінченного 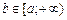, так що існує.

Означення. Границя при називається невласним інтегралом від функції f(x) на нескінченному проміжку і позначається так: .

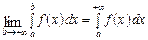Якщо ця границя існує та скінченна, то невласний інтеграл називається збіжним, а якщо не існує (зокрема нескінченна), то — розбіжним.

Якщо f (x) — інтегровна для скінченних a та b, тобто формули для обчислення невласних інтегралів на нескінченному проміжку мають вигляд:

(30.1)

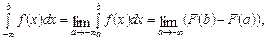(30.2)

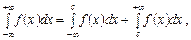(30.3)

де

Приклад. Дослідити на збіжність інтеграл Діріхле

. (30.4)

Для розв’язування задачі розглянемо такі три випадки:

I. р = 1. 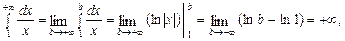інтеграл розбіжний.

II. p < 1. , інтеграл розбіжний.

III. p > 1.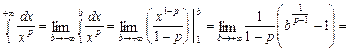

, інтеграл збіжний.

Отже, інтеграл Діріхле збіжний при p > 1 та розбіжний при .

Крім безпосереднього обчислення невласних інтегралів при дослідженні їх на збіжність існують і інші методи.

Одним із таких методів можна встановити збіжність інтеграла Пуассона (рис. 30.1)

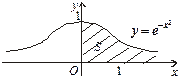Рис. 30.1

, (30.5)

особливість якого полягає в тому, що первісна для підінтегральної функ­ції не виражається через елементарні функції.

У деяких випадках достатньо вста­новити лише збіжність чи розбіжність розглядуваного інтеграла, при цьому можна скористатися методом порівняння, що базується на такій теоремі:

Дата добавления: 2014-11-29