КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площа поверхні обертання
|
|
|
|
Завдання для самостійної роботи
Розв’язання
Рівняння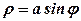 
задає коло діаметра 
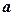з центром у точці 
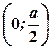. Зрозуміло, що 
. 
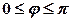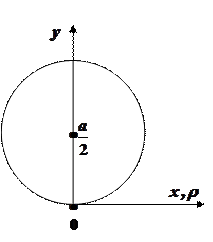Для обчислення об’єму використаємо формулу (29.6). Будемо мати:
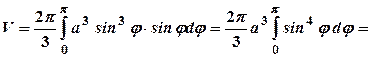
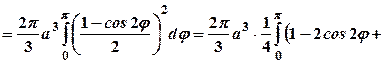
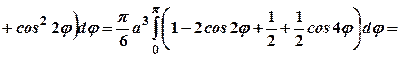
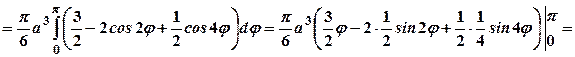
куб. од.
Обчислити об’єми тіл, утворених обертанням плоских фігур навколо координатних осей:
1. 
, 
, 
, 
, 
?
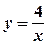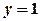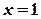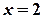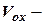2. 
, 
, ?
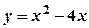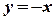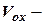3. 
, 
, 
?
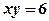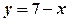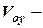4. 
, 
, ?
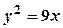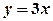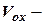5. 
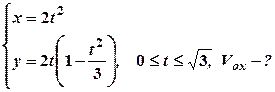
6. Знайти об’єм тіла, утвореного обертанням кривої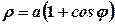 
навколо полярної осі 
.
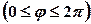Обчислити об’єм тіла, утвореного обертанням фігури, що обмежена лініями:
16. 
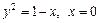навколо осі Оу.
Відповідь.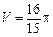 
.
17. 
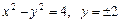навколо осі Оу.
Відповідь.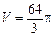 
.
18. 
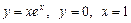навколо осі Ох.
Відповідь.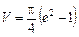 
.
19. 
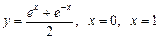навколо осі Ох.
Відповідь.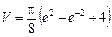 
.
20. ху = 4, х = 1, х = 4, у = 0 навколо осі Ох.
Відповідь.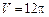 
.
Площа поверхні, утвореної обертанням навколо осі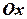 
дуги гладкої кривої, заданої функцією 
, 
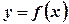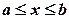, обчислюється за формулою
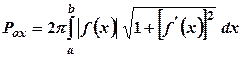. (29.7)
Якщо гладка крива задана рівнянням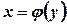 
, 
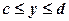, то площа поверхні, утвореної обертанням кривої навколо осі 
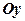, може бути обчислена за формулою
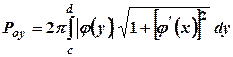. (29.8)
У разі параметричного задання кривої рівняннями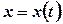 
, 
, 
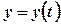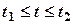, де функції 
, 
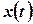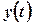- неперервні разом із своїми похідними, відповідні площі поверхні обчислюються за формулами:
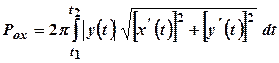, (29.9)
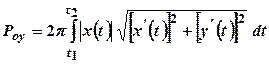. (29.10)
Площа поверхні, отриманої обертанням навколо полярної осі криволінійного сектора, обмеженого неперервною кривою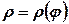 
та двома полярними радіусами 
, 
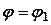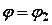, визначається за формулою
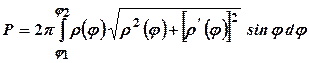. (29.11)
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1479; Нарушение авторских прав?; Мы поможем в написании вашей работы!