Приклади. 1). Знайти кривизну кола радіуса R в довільній точці

1). Знайти кривизну кола радіуса R в довільній точці.

Розв’язання.

Візьмемо на колі дві довільні точки М і М' і проведемо в них дотичні до кола. Довжина дуги ММ' кола ∆s = R ∆α. Тому середня кривизна

│ │ = є сталою. Тоді і │ │ = . Отже, кривизна кола в кожній точці стала: К = . Звідси випливає, що чим менший радіус кола, тим більша кривизна, і навпаки, чим більший радіус кола, тим менша його кривизна.

2). Знайти кривизну прямої лінії.

Розв’язання.

У цьому разі дотична в кожній точці збігається із заданою прямою. Тому кут її повороту ∆α = 0.Середня кривизна │ │ = 0, а отже, і │ │ = 0. Таким чином, кривизна прямої в кожній її точці дорівнює нулю.

Виведемо тепер формули для обчислення кривизни кривих, заданих в різних системах координат. Нехай криву задано в декартовій системі координат рівнянням у = f(х), де функція f(х) на відрізку [a;b] має похідні до другого порядку включно.

Скористаємося формулою(4). Очевидно, що коли М'→М, то довжина дуги ∆s → 0. Тому формулу (4) можна записати ще так:

К = │ │ (5)

Крім того, позначивши через α кут, утворений дотичною до кривої у точці М(х; f(х)) з додатнім напрямом осі Ох, дістанемо

tg α = f '(х).

Звідси

α = arctg f '(х),

dα = 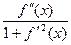dх

Підставляючи у формулу (5) значення dα і значення ds із формули(1), дістаємо формулу для кривизни кривої

К = (6)

З цієї формули легко дістати формулу для кривизни кривої, коли остання задана параметричними рівняннями х = х(t), у = у(t). Справді, якщо функції х = х(t), у = у(t) мають на відрізку [α; β] похідні до другого порядку включно і х'(t) ≠ 0, то

у_х' = ,

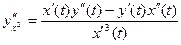
Тоді, підставляючи значення у формулу (6) відповідно замість f ''(х), f '(х),дістанемо формулу

К = (7)

Якщо криву задано в полярній системі координат рівнянням ρ = ρ(φ), α ≤ φ ≤ β, то поклавши φ = t, матимемо параметричні рівняння кривої

х = ρ(φ) соs φ, у = ρ(φ) sіn.φ

Знаходячи відповідні похідні і підставляючи їх у формулу (7), матимемо формулу для кривизни кривої:

К = (8

Означення3. Величину, обернену до кривизни кривої в даній точці, називають радіусом кривизни кривої і позначають

R = .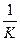

Означення 4. Коло, радіус якого дорівнює радіусу кривизни в даній точці, називають колом кривизни.

Дата добавления: 2014-11-29