Как объекта управления

МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКОГО ПРОЦЕССА

Непрерывный поток фермента регулируется по измеренному значению концентрации субстрата (рис.1). Это управление используется как вспомогательный процесс в турбодиметрии для непрерывной подачи субстрата.

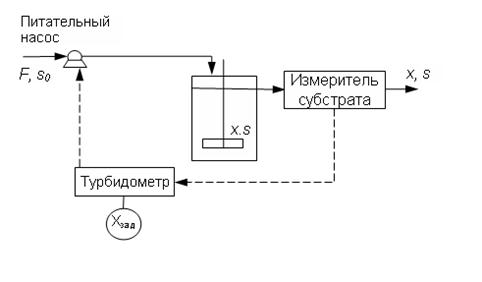
Рисунок 7.1- Принципиальная схема управления скоростью подачи субстрата в непрерывном потоке.

Математическое описание рассматриваемого процесса может быть представлено в следующем виде[1]:

- для удельной скорости роста: µ=µ_m·S/(K_S+S+S²/K_I)

- для субстрата: dS/dt = F*(Sвхода-S)-µ·X/Y,

- для биомассы: dX/dt = -F*X/V+μ·X,

- Для концентрации продукта в соответствии с законом Luedeking-Piret запишем уравнение в следующем виде: dP/dt = -F·P/V+(B+A·µ)·X.

Граничные условия: Sвхода=const.

Начальные условия: при t=0 S(0)=S0,X(0)=X0,P(0)=P0.

Управление концентрацией субстрата осуществляется с помощью пропорционально-интегрального регулятора подачей свежего входного потока по уравнению: F=F₀+K_P·ε +K_P/τ_I ∫ε dt, где ε =(S-Szad).Это уравнение после дифференцирования по t было представлено в программном продукте в виде соответствующего дифференциального уравнения. Для оценивания качества регулирования здесь используется критерий в виде: 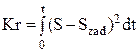. В таблице 7.1 дана спецификация принятых обозначений и численные значения основных параметров, входящих в математическое описание. В таблице 7.2 приведена спецификация индексов.

Таблица 7.1.Спецификация и численные значения параметров.

Символы	Наименование	Размерность	Численное значение
F	Объемный расход потока	м^3/ч
F0	Нормальный объемный расход потока	м^3/ч	0.4
KP	Пропорциональная составляющая регулятора	м^6/(ч× кг)
KI	Константа подавления	кг/м³	2.2
KS	Константа насыщения	кг/м³	0.12
S	Концентрация субстрата	кг/м³	0.01
S0	Концентрация субстрата во входном потоке	кг/м³
V	Объем реактора	м^3
X	Концентрация биомассы	кг/м³	0.1
Y	Коэффициент выхода	кг/кг	0.5
ε	Рассогласование	кг/м³
μ	Определенный темп рост	1/ч
τI	Время изодрома	ч	1.5

На рисунках 7.2-7.3 представлены протоколы моделирования рассматриваемого процесса в системе компьютерной математики MathCad

Рисунок 7.2- Протокол моделирования управления процессом для заданного значения концентрации субстрата (начало)

Таблица 7. 2.Спецификация индексов.

Индексы	Наименование
m	Максимальное значение
zad	Заданная точка

.

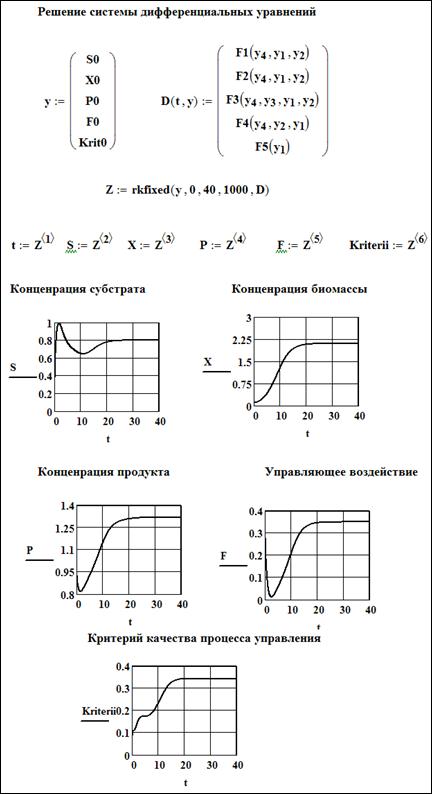
Рисунок 7.3 - Результаты моделирования управления процессом для заданного значения концентрации субстрата.

Дата добавления: 2014-11-29