Каскадом реакторов с противоточным охлаждением

МОДЕЛИРОВАНИЕ ПРОЦЕССА УПРАВЛЕНИЯ

В каскаде реакторов непрерывного действия с мешалками осуществления экзотермическая реакция первого порядка. Реакторы снабжены рубашками для противоточного охлаждения водой.

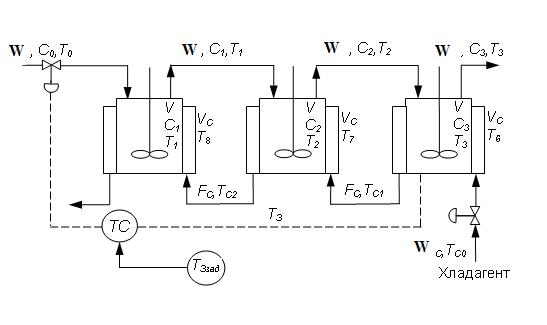
Рисунок 8.1- Трехступенчатый каскад реакторов с

противоточным охлаждением

Математическое описание процесса может быть представлено в следующем виде:

Для кинетики процесса известно, что: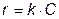

Уравнение материального баланса для 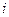-го реактора имеет вид:

,

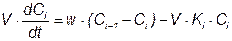где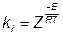

Уравнение теплового баланса для 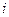-го реактора имеет вид:

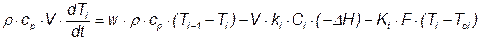
Энергетический баланс для охлаждающей рубашки в 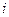-том реакторе имеет вид:

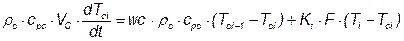
Таблица 8.1 – Спецификация принятых обозначений и их размерность

Обозначения	Наименование	Размерность
	Поверхность теплообмена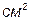
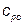
	Удельная теплоемкость хладагента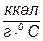
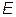
	Энергия активации
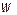
	Объемный расход потока в реактор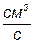
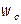
	Расход хладагента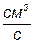
	Газовая постоянная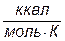
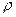
	Плотность (принята равной 1)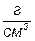
	Плотность хладагента (принята равной 1)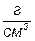
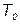
	Начальная температура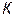
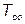
	Начальная температура хладагента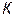
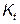
	Коэффициент теплопередачи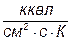
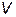
	Объем реактора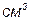
	Объем рубашки реактора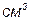
	Предэкспоненциальный множитель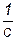
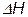
	Теплота реакции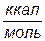

Рассмотрим управление температурой в третьем реакторе изменением подачи исходной смеси в начало процесса. Используется принцип управления по отклонению, в данном случае по отклонению температуры в третьем реакторе от заданного значения. Управление осуществляется с помощью управляющего воздействия 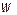, которое изменяется по закону пропорционально-интегрального регулятора. Уравнение регулятора для пропорционально-интегрального регулирования имеет вид:

, .

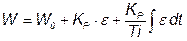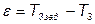Для моделирования этого закона управления в Mathcad он был приведен к соответствующему дифференциальному уравнению. Для оценки качества управления был использован критерий качества в виде:

,

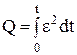который также был приведен к дифференциальному уравнению.

Ниже приведен протокол поиска оптимальных настроек регулятора в системе компьютерной математики Mathcad. При решении дифференциальных уравнений использовался метод Эйлера.Поиск оптимальных настроек осуществлялся с помощью процедуры Minimize для минимизации значения критерия качества регулирования.

Рисунок 8.2- Протокол поиска оптимальных настроек регулятора температуры в каскаде реакторов (начало)

Рисунок 8.3- Протокол поиска оптимальных настроек регулятора температуры в каскаде реакторов (продолжение)

Рисунок 8.4- Протокол поиска оптимальных настроек регулятора температуры в каскаде реакторов (продолжение)

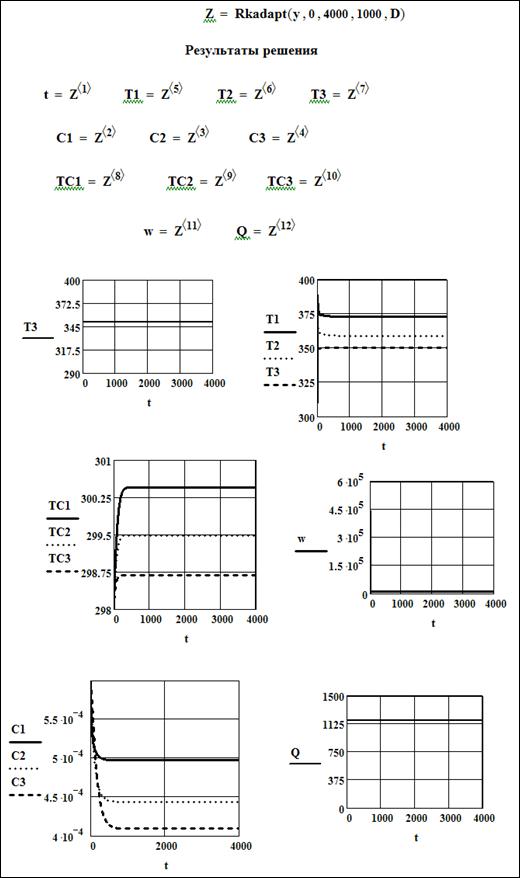
Рисунок 8.5- результаты поиска оптимальных настроек регулятора температуры в каскаде реакторов

Рассмотрим управление температурой в третьем реакторе изменением подачи хладагента в охлаждающую рубашку третьего реактора. Как и ранее используется принцип управления по отклонению температуры в третьем реакторе от заданного значения. Управление осуществляется с помощью управляющего воздействия 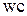, которое изменяется по закону пропорционально-интегрального регулятора. Уравнение регулятора для пропорционально-интегрального регулирования имеет вид:

, .

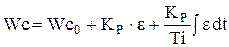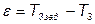Для моделирования этого закона управления в Mathcad он был приведен к соответствующему дифференциальному уравнению. Для оценки качества управления, как и ранее, был использован критерий качества в виде:

,

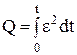который также был приведен к дифференциальному уравнению.

Ниже приведен протокол поиска оптимальных настроек регулятора в системе компьютерной математики Mathcad. При решении дифференциальных уравнений использовался метод Эйлера.Поиск оптимальных настроек осуществлялся с помощью процедуры Minimize для минимизации значения критерия качества регулирования.

Рисунок 8.6-Протокол моделирования управление температурой в третьем реакторе изменением подачи хладагента в охлаждающую рубашку третьего реактора (начало)

Рисунок 8.7- Протокол моделирования управление температурой в третьем реакторе изменением подачи хладагента в охлаждающую рубашку третьего реактора (продолжение)

Рисунок 8.8- Протокол моделирования управление температурой в третьем реакторе изменением подачи хладагента в охлаждающую рубашку третьего реактора (продолжение)

Рисунок 8.9- Результаты моделирования управление температурой в третьем реакторе изменением подачи хладагента в охлаждающую рубашку третьего реактора

Дата добавления: 2014-11-29