Достоверность разности долей

Достоверность разности выборочных долей определяется так же, как и для разности средних:

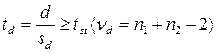(10.34)

где:

t_d – критерий достоверности разности;

d = p₁ – p₂ – разность выборочных долей;

– ошибка разности долей, равная корню квадратному из суммы квадратов ошибок сравниваемых долей.

Если требуется определить только достоверность разности, то квадраты ошибок долей определяются непосредственно:

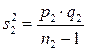; ; (10.35)

t_st – стандартное значение критерия определяется так же, как и для разности средних – по таблице стандартных значений критерия Стьюдента или по приближенным формулам, исходя из требуемой вероятности безошибочных прогнозов (b₁ = 0,95, b₂ = 0,99,
b₃ = 0,999) и числа степени свободы разности;

n – число степеней свободы разности, равное сумме объемов сравниваемых выборок n₁ и n₂ без двух.

Пример

При изучении планктона оказалось, что из 8 особей одного вида 7 были самцами, а из 7 экземпляров другого родственного вида самцами были только 2. Можно ли на основании этих данных сделать заключение, что у первого вида доля самцов в данном сезоне выше, чем у второго?

Произведены следующие расчеты:

p₁ = 7/8 = 0,88; ;

p₂ = 2/7 = 0,29; ;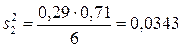

d =0,88 – 0,29 = 0,59; ;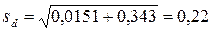

; n = 8 + 7 – 2 = 13; t_st={2,2 – 3,0 – 4,1}.

Оказалось, что разница между видами по относительной доле (%) самцов даже при сравнении долей в таких малых выборках превышает нижний порог достоверности. Поэтому с достаточной для первой ориентировки уверенностью можно заключить, что процент самцов в данном сезоне у первого вида больше, чем у второго.

Пример

При изучении заболеваемости гипертонией выяснено, что от здоровых родителей из 580 сыновей болело 197, а от родителей обоих гипертоников из 39 сыновей болело 28. Можно ли считать, что гипертония поражает сыновей, происходящих от гипертоников, чаще, чем сыновей от здоровых родителей не только среди обследованных сыновей, но и вообще среди всех мужчин?

p₁ = 197/580 =0,34; ;

p₂ = 28/39 = 0,72; ;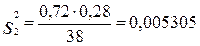

d = 0,72 – 0,34 = 0,38; ;

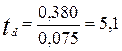; n = 580 + 39 – 2 = 617; t_st = {2,0 – 2,6 – 3,3}.

Разность оказалась в высшей степени достоверной. Сыновья гипертоников вообще явно чаще болеют гипертонией по сравнению с сыновьями от обоих здоровых родителей.

Вопросы для самоконтроля

1 Какие три величины необходимы для оценки генерального параметра?

2 Перечислите три основных порога вероятности безошибочных прогнозов.

3 Укажите значения критериев надежности для основных порогов вероятности безошибочных прогнозов при условии достаточно больших выборок.

4 Напишите формулы ошибок репрезентативности основных выборочных показателей.

5 Какие процедуры необходимо выполнить, чтобы оценить генеральный параметр для количественных признаков в форме доверительных границ? Привести примеры.

6 Как определяется недостоверная и достоверная оценка средней разности?

7 Напишите формулу для определения критерия достоверности разности.

8 Напишите формулу ошибку репрезентативности доли при изучении качественных признаков.

9 Напишите формулу ошибки достоверность разности выборочных долей.

ТЕМА 11 Парная корреляция

11.1 Коэффициент корреляции

11.2 Ошибка коэффициента корреляции

11.3 Уравнение прямолинейной регрессии. Коэффициент прямолинейной регрессии

11.4 Ошибки элементов уравнения прямолинейной регрессии

Дата добавления: 2014-11-29