Достоверность выборочного коэффициента корреляции

Критерий выборочного коэффициента корреляции определяется по формуле:

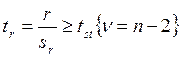(11.9)

где:

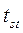– критерий достоверности коэффициента корреляции;

r – выборочный коэффициент корреляции;

n – число коррелированных пар данных;

t_st – стандартное значение критерия Стьюдента, определяемое по таблице для установленного числа степеней свободы и порога вероятности безошибочных прогнозов.

При t ≥ t_st коэффициент корреляции достоверен. В этом случае с определенной вероятностью можно считать, что между коррелируемыми признаками имеется связь и в генеральной совокупности такая же по знаку, какая получилась в выборке (прямая или обратная).

При t < t_st выборочный коэффициент корреляции недостоверен, что не дает возможности сделать какое-либо заключение о связи признаков в генеральной совокупности. Для выяснения этого вопроса требуется провести повторные исследования на более многочисленном материале.

Пример

При проверке гипотезы о связи крупноплодности с жирномолочностью был рассчитан коэффициент корреляции между процентом жира в молоке у 50 коров и весом при рождении телят от этих же коров. Получено:

коэффициент корреляции: r = +0,21;

его ошибка: ;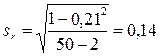

критерий достоверности: 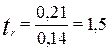; n = 48;

t_st = {2,0 – 2,7 –3,5}.

Выборочный коэффициент оказался явно недостоверным. На основе проведенного исследования нельзя ожидать связи между крупноплодностью и жирномолочностью у всех коров вообще.

Определение достоверности коэффициента корреляции можно значительно упростить, используя свойства особой функции предложенной Фишером:

(11.10)

При помощи этой функции можно заранее определить, при каком объеме выборки коэффициент корреляции определенной величины будет достоверен по требуемому порогу вероятности безошибочных прогнозов, по следующей формуле:

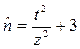, (11.11)

где:

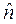– количество пар значений, достаточное для достоверности выборочного коэффициента корреляции,

t – критерий Стьюдента для каждого из трех порогов вероятности безошибочных прогнозов (b₁ = 0,95, b₂ = 0,99, b₃ = 0,999), для больших групп: t₁ = 1,96, t₂ =2,58, t₃ = 3,30.

z – функция Фишера

По этой формуле рассчитано значение z и количество пар значений, достаточное для достоверности выборочного коэффициента корреляции для каждого из трех порогов вероятности безошибочных прогнозов.

В примере в выборке объемом n = 50 получен коэффициент корреляции r = +0,21.

При r = 0,21, рассчитаны три числа: 87 – 149 – 242. Это значит, что выборочный коэффициент корреляции, равный r = 0,21, может стать достоверным в том случае, если объем выборки (число коррелируемых пар данных) будет: для первого порога вероятности 87, для второго – 149, для третьего – 242. Так как фактический объем выборки n = 50 далеко не достигает первого, максимальною порога, то полученный коэффициент корреляции оказался недостоверным, что было найдено и обычным способом.

Объем выборки для первого порога вероятности безошибочных прогнозов b₁ = 0,95 можно оценить, воспользовавшись простым соотношением: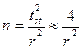

Дата добавления: 2014-11-29