Ошибка репрезентативности корреляционного отношения

Еще не разработано точной формулы ошибки репрезентативности корреляционного отношения. Обычно приводимая в учебниках формула имеет недостатки, которыми не всегда можно пренебречь. Эта формула не учитывает числа классов, по которым рассчитывается корреляционное отношение:

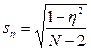(13.7)

Если один и тот же материал разбить по первому признаку (аргументу) на большое или малое число классов, то это различие в числе классов очень заметно скажется на величине выборочного показателя криволинейной связи и на его достоверности.

В настоящее время можно использовать примерное значение ошибки не самого корреляционного отношения, а его квадрата η²:

(13.8)

где:

– ошибка квадрата корреляционного отношения;

g – число классов первого признака;

N – объем выборки.

При использовании этой ошибки для определения критерия достоверности и доверительных границ квадрата корреляционного отношения вместо критерия Стьюдента следует брать преобразованный критерий Фишера (F), применяющийся в дисперсионном анализе как критерий достоверности показателей силы влияния.

Критерий, достоверности (F) и доверительные границы квадрата корреляционного отношения 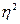определяются по следующим формулам:

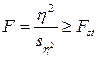, (13.9)

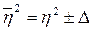, (13.10)

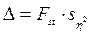(13.11)

В этих формулах:

F – критерий достоверности квадрата корреляционного отношения, основанный на применении примерной формулы ошибки этого показателя. Этот критерий в точности равен критерию Фишера;

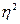– квадрат корреляционного отношения;

– ошибка репрезентативности квадрата корреляционного отношения;

ν₁ = g– 1 – первое число степеней свободы, равное числу классов первого признака без одного;

ν₂ = N–g – второе число степеней свободы, равное объему корреляционной решетки минус число классов первого признака;

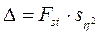– погрешность, возможная при оценке генерального значения корреляционного отношения;

F_st – стандартные значения преобразованного критерия Фишера для трех порогов вероятности безошибочных прогнозов и для двух степеней свободы.

Пример

Получены показатели N = 21, η² = 0,76, g = 5 (число классов первого признака).

Ошибка репрезентативности квадрата корреляционного отношения:

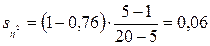
Критерий достоверности:

F = 0,75/0.06 = 12,7; ν₁ = 5–1 = 4; ν₂ = 21–5 = 16;

F_st = (3,0–4,8–7,9).

Возможная погрешность в оценке генерального параметра:

.

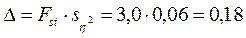Доверительные границы квадрата корреляционного отношения:

η² = 0,76 ± 0,18 не более 0,76 + 0,18 = 0,94;

не менее 0,76 – 0,18 = 0,58

Доверительные границы корреляционного отношения:

η = ( – 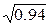) = (0,76 – 0,97).

Дата добавления: 2014-11-29