Критерий линейности корреляции

Для определения степени приближения криволинейной зависимости к прямолинейной используется критерий F, вычисляемый по формуле:

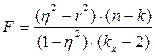(13.12)

где:

η² – квадрат корреляционного отношения Y по Х;

r² – квадрат коэффициента линейной корреляции;

n – объем выборки;

k_x – число групп по ряду X.

Связь можно практически принять за линейную, если
F_факт < F_теор, и определять показатели для прямолинейной корреляции и регрессии. Корреляция нелинейная, если F_факт ≥ F_теор. Теоретические значения F берутся из таблицы приложений для
ν₁ = k_x – 2 и ν₂ = n – 2 степеней свободы.

Криволинейные зависимости между двумя переменными могут быть выражены в виде кривых линий регрессии и соответствующих им математических уравнений. Эмпирические точки поля регрессии при криволинейной корреляции располагаются около кривых различного типа – парабол, гипербол, логарифмических кривых и т. п.

В общем случае все линии регрессии являются кривыми и рассматриваемая нами ранее линейная регрессия является простейшей зависимостью между двумя признаками.

Основной метод построения математических уравнений: подбор типа формулы и нахождение коэффициента к ней.

Статистическая обработка экспериментального материала часто приводит к полиному второй степени:

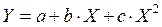(13.13)

Вопросы для самоконтроля

1 Назначение корреляционного отношения. Характеризует ли корреляционное отношение степень криволинейной связи между двумя парными выборками?

2 Дайте определение группового среднего и квадратов отклонений группового варьирования.

3 Напишите формулу, определяющую корреляционное отношение при большом числе наблюдений (>30).

4 В каких пределах заключено значение корреляционного отношения?

5 Что показывает отношение сумм квадратов группового варьирования к общему ()? Название этого статистического показателя.

6 Одинаковую ли меру связи признаков (первого со вторым и второго с первым) дает коэффициент корреляции и корреляционное отношение?

7 Какой критерий следует брать для определения достоверности и доверительных границ квадрата корреляционного отношения?

8 Что является критерием линейности или нелинейности связи между парными признаками?

9 Какими функциями могут быть аппроксимированы криволинейные зависимости между двумя переменными? Приведите примеры.

ТЕМА 14 Однофакторный дисперсионный анализ

14.1 Сущность и метод дисперсионного анализа

14.2 Однофакторные статистические комплексы

Дата добавления: 2014-11-29