Следствия из свойств

Свойства скалярного произведения

1^о 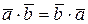– переместительный закон.

2^о 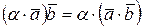– сочетательный закон.

3^о .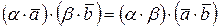

4^о 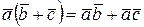– распределительный закон.

5^о Если 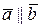, то 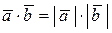, в частности, при скалярном умножении вектора самого на себя получается квадрат его модуля, т.е. 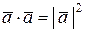(скалярный квадрат вектора равен квадрату его модуля).

6^о Скалярное произведение двух векторов обращается в нуль тогда и только тогда, когда эти векторы взаимно перпендикулярны.

7^о Если векторы 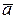и 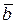заданы своими координатами: 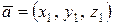, , 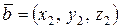то скалярное произведение их определяется формулой .

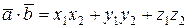1^о Необходимым и достаточным условием перпендикулярности векторов 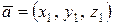и 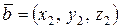является равенство

.

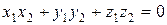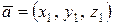2⁰ Угол между векторами и 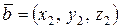определяется соотношением:

.

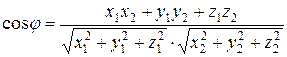3^о Если некоторая ось 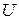составляет с координатными осями углы 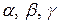, то проекция произвольного вектора 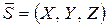на эту ось будет равна:

.

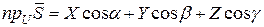4^о Проекция вектора 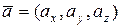на вектор 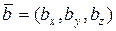находится по формуле:

.

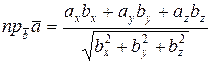Пример 3.1. Даны три точк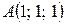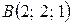и , и . Найти угол a) 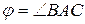; б) проекцию вектора 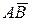на вектор .

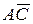Решение.

Найдем векторы 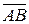и :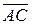

, .

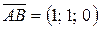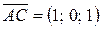a) .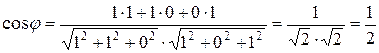

Следовательно, .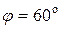

б) .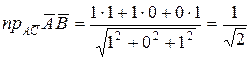

Пример 3.2. Даны векторы 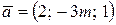и 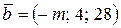. При каком значении 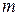эти векторы перпендикулярны?

Решение.

Из свойства 6^о скалярного произведения векторов следует, что для того чтобы векторы 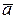и 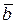были перпендикулярны, необходимо, чтобы 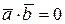. Найдем скалярное произведение векторов 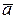и :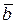

,

.

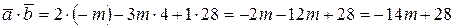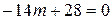Откуда .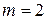

Пример 3.3. Найти вектор 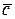, коллинеарный вектору 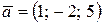и удовлетворяющий условию .

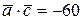Решение. Так как вектор 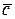коллинеарен вектору 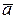, то его координаты пропорциональны и могут быть следующими: 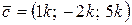. Тогда скалярное произведение этих векторов

,

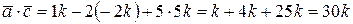а по условию 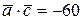, откуда

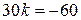, т.е. .

Следовательно, координаты вектора .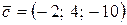

Пример 3.4. Какой угол образуют единичные векторы 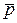и 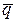, если векторы 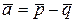и 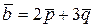взаимно перпендикулярны.

Решение.

Так как векторы 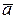и 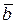взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е.

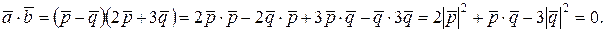
По условию задачи векторы 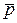и 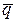единичные, т.е. 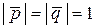, тогда последнее соотношение можно переписать иначе:

.

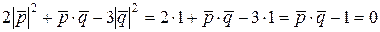Откуда

.

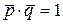По формуле скалярного произведения двух векторов

,

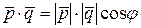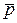где – угол между векторами и 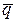. Тогда

.

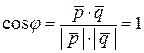Следовательно, угол 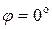(векторы коллинеарны).

Дата добавления: 2014-11-29