Синтез логических схем 1 страница

Различные логические функции отражают условия работы компью­тера и возможный его состав, если каждой элементарной логической опе­рации ставится в соответствие реальный физический элемент. Это озна­чает, что логические функции можно использовать в качестве тех анали­тических форм, по которым строятся логические схемы различных узлов ЭВМ. Любая сложная логическая функ­ция может быть выражена через элементарные функции, со­ставляющие функционально полную систему. Любая сложная логическая функция может представлять собой реализа­цию некоторой части компьютера, если эта часть построена с помощью набора элемен­тов, реализующего все функции одной из функционально полных систем. Набор элементов, отвечающий любой функционально полной системе элементарных логических функций, называется функ­ционально полным набором логических элементов [2].

Для построения узлов компьютера чаще всего используются эле­менты, обеспечивающие реализацию таких элементарных логических опе­раций (функций), как отрицание, конъюнкция, дизъюнкция, опера­ция Шеффера и операция Пирса.

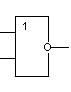
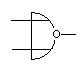
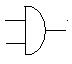
Логические элементы именуются в соответствии с реализуемы­ми функциями. Для реализации отрицания используется инвертор (элемент НЕ), для реализации конъюнкции — конъюнктор (эле­мент И), для реализа­ции дизъюнкции — дизъюнктор (элемент ИЛИ), для реализации операции Шеффера — элемент Шеффера (элемент И — НЕ), для реализа­ции операции Пирса — элемент Пирса (элемент ИЛИ — НЕ).

Для реализации логических функций, заданных своими дизъюнк­тивными нормальными формами, можно использовать набор элементов И, ИЛИ, НЕ. Элементы И реализуют элементарные конъюнк­ции, элементы ИЛИ — дизъюнкции, элементы НЕ исполь­зуются для инвертирования значений соответствующих переменных. Ясно, что реализация д. н. ф. возможна только тогда, когда элементы И имеют количество входов, не меньшее ранга реализуе­мых конъюнкций, а элемент ИЛИ имеет количе­ство входов, не мень­шее числа конъюнкций в реализуемой д. н. ф. Если эти условия не выполня­ются, то конъюнкции и дизъюнкция реализуются по ча­стям, что услож­няет общую логическую схему; к усложнению схемы ведет и увеличение числа конъюнкций в д. н. ф., так как для реализации каждой конъюнкции требуется, по крайней мере, один элемент И. Следо­вательно, в общем слу­чае более простой логиче­ской функции отвечает и более простая логиче­ская схема. Для упрощения начальных форм логиче­ских функций прово­дятся спе­циальные действия, или минимизация логи­ческих функций.

Основная цель минимизации логических функций — получение их минимальных нормальных форм, дизъюнктивных или конъюнктивных. В общем случае минимальная форма опреде­ляется следующим образом: дизъюнктивная или конъюнктивная нормальная форма логической функ­ции называется минимальной, если она содержит наименьшее число дво­ичных переменных, их отрицаний и логических операций по сравнению со всеми другими эквивалентными дизъюнктив­ными или соответственно конъюнктив­ными нормальными формами.

Если число переменных мало 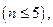то минимизация логических функций может быть осуществлена вручную путем непосредственных преоб­разований. Ми­ними­зация сложных логических функций проводится, как правило, с использо­ванием машинных методов, т. е. путем реализации соот­ветствующих алго­ритмов на ЭВМ.

Непосредственное преобразование состоит в том, что мини­мизация исходной логической функции осуществляется в результате понижения ранга конъюнкций (дизъюнкций) в результате использования основных законов алгебры логики, их следствий или же логических тождеств, на­пример 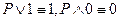, или же 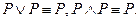При проведении экви­ва­лентных преобразований необходимо получить минимальную фор­му функции (формулы), т. е. такую, которая не содержит «лишних» двоичных переменных и «лишних» членов. При этом «лишними» дво­ичными пере­менными и членами логической формулы называются такие, значения ко­торых не влияют на значение преобразуемой формулы. Так, например, в формуле 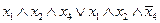лишней является переменная т. к. значе­ние истинности рассматриваемой функции не зависит от значе­ний этой переменной. Покажем, что это действительно так:

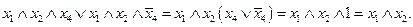
В приведенном примере мы провели так называемую «склейку», т.е. удалили элемент 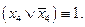Отметим, что на последнем этапе преобразова­ний возможно удаление «лишних» членов с помощью приме­нения операции «обобщенной склейки». Поясним это на следующем при­мере.

Пусть имеется Д. Н. Ф. 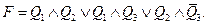Рассмотрим таблицу ис­тинности для функции 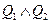при различных значениях 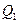и :

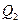Операция	Значения функции

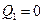
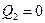
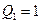
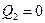
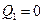
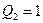
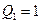
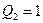
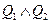
В первом случае

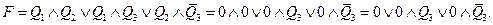
Во втором:

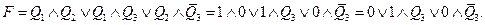
В третьем:

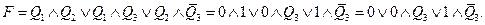
И в четвертом случае

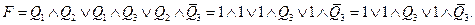
Отсюда видно, что значение истинности Д. Н. Ф. не зависит от зна­чения 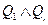а тогда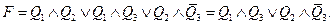

Синтез логической схемы заключается в ее построении по задан­ным условиям работы соответствующего узла компьютера. Эти усло­вия опре­деляют количество входов и выходов узла, а также закон соответствия на­боров входных и выходных сигналов. Алгоритм синтеза может включать в себя следующие шаги:

1. Формирование логических условий работы рас­сматривае­мого узла пу­тем составления таблицы его работы, или таблицы истинно­сти, для соот­ветствующих логических функций. Таблица работы узла со­ставляется не­посредственно по заданным условиям его работы.

2. Получение по таблицам истинности аналитических пред­ставлений логи­ческих функций, описывающих рассматриваемый узел, в виде совер­шенных д. н. ф. или к. н. ф.

3. Минимизация логических функций, проводимая с целью по­луче­ния в конечном итоге наиболее простой логической схемы. Минимизиро­ванные функции приводятся к виду, который отвечает наиболее простой их реали­зации с помощью логических элементов заданного набора.

4. Построение логической схемы по минимизированным логическим функ­циям.

При проведении работ по синтезу логических схем могут выпол­няться не все действия из указанных четырех, или же логические функции, описывающие рассматриваемый узел заданы. Если же логические функ­ции не поддаются минимизации, то действия по третьему пункту сводятся к пре­образованию функций с целью получения их форм, удобных для реа­лизации посредством логических элементов заданного на­бора. Следует заметить, что при синтезе схем, описывающих работу какого-либо узла компьютера, чаще используют элементарные конъюнкции и, соответст­венно, С. Д. Н. Ф. в силу того, что в этом случае удобнее проводить необ­ходимые преобразования. В этом случае обычно стараются выявить так называемые «соседние» [2] конъюнкции, т.е. элементарные конъюнкции одного ранга состоящие из одних и тех же логических переменных и от­личающихся инвертированием только одной переменной, т.е. если в неко­торую конъюнкцию входит переменная 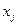, то в «соседнюю» входит 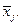На­пример, конъюнкци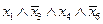и и 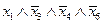являются «сосед­ними».

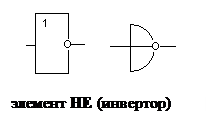
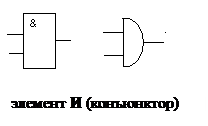
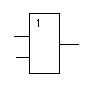
Ниже рассмотрим примеры синтеза схем, но, прежде чем начать рас­смотрение этих примеров, приведем примеры условных обозначений при­нятые для наиболее часто используемых элементов.

элемент ИЛИ (дизъюнктор)

элемент Пирса (ИЛИ-НЕ)

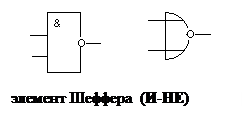Рисунок 1

Так как работа некоторого узла компьютера задается таблицей ис­тинности, сформулируем правила, по которым производится построение дизъюнктивных и конъюнктивных нормальных форм [2]:

Правило 1. Для построения совершенной дизъюнктивной нормальной формы логической функции от 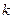двоичных переменных, заданной табли­цей истинности, необходимо по каждому набору двоичных переменных, на котором функция принимает значение единицы, записать конъюнкцию 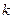-го ранга, включающую все переменные, и полученные конъюнкции со­единить знаками дизъюнкции; при записи конъюнкций двоичные пере­менные равные нулю инвертируются, т.е. в конъюнкцию включаются их отрицания, а остальные включаются без изменений.

Правило 2. Для построения совершенной конъюнктивной нормальной формы логической функции от 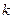двоичных переменных, заданной табли­цей истинности, необходимо по каждому набору двоичных переменных, на котором функция принимает значение нуля, записать дизъюнкцию 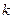-го ранга, включающую все переменные, и полученные дизъюнкции соеди­нить знаками конъюнкции; при записи дизъюнкций двоичные переменные равные единице инвертируются, т.е. в дизъюнкцию включаются их отри­цания, а остальные включаются без изменений.

Теперь мы можем приступить к примерам реализации схем. В пер­вом примере приводится устройство, имеющее 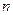входов и один выход. Та­кие устройства носят название мультиплексоров. Работа простейшего мультиплексора на три входа задана таблицей истинности [2]:

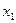
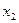
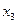
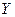
Согласно правилу, приведенному выше, выпишем элементарные конъ­юнкции[1]: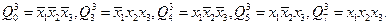

Тогда 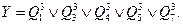Несложно подсчитать, что для реализации данной логической схемы потребуется пять конъюнкторов (И), семь ин­верторов (отрицаний, НЕ) и один дизъюнктор (ИЛИ), т.е. тринадцать эле­ментов, поэтому проведем минимизацию.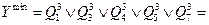

выделим соседние конъюнкции и добавим «лишнюю» конъюнкцию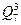

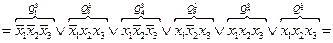
проведем группировку

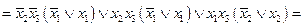
после проведения «склейки», получаем

.

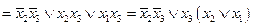При реализации последней схемы требуется уже два инвертора, две схемы ИЛИ и два элемента И, т. е. всего шесть элементов. Если же использовать закон инверсии для дизъюнкции, то 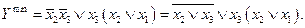Для последнего варианта потребу­ется три схемы ИЛИ, одна НЕ и одна И, т. е. пять элементов. Блок-схема устройства имеет вид

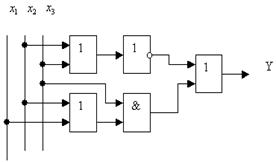Рисунок 2

Теперь рассмотрим вариант минимизации и синтеза данной схемы с использованием с. к. н. ф.

В этом случае 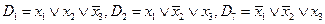и

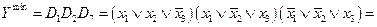
в этом случае на начальном этапе минимизации мы можем применять только законы алгебры логики

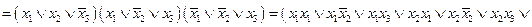
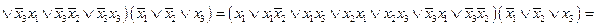
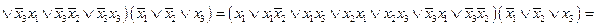
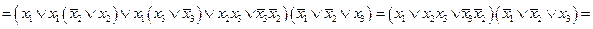
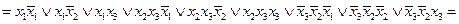
теперь можно провести группировки, а затем и склейки с целью пониже­ния ранга дизъюнкций

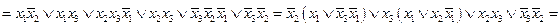
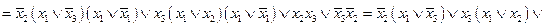
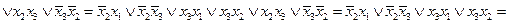
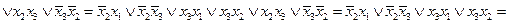
после проведения обобщенной склейки получим

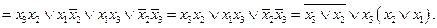
В результате мы получили ту же самую конечную функцию, проведя значительно больше преобразований и затратив существенно больше уси­лий, нежели в первом случае. Последний пример прекрасно иллюстрирует тот факт, почему обычно при проектировании различных устройств обычно проводят минимизацию дизъюнктивных, а не конъюнктивных со­вершенных нормальных форм, о чем уже говорилось выше.

Этап минимизации логических функций имеет особенности так­же тогда, когда производится синтез схем с несколькими выхода­ми. Такие схемы называют 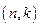- полюсниками, считая 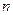количе­ством входов, а 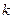— количеством выходов. Для получения наиболее простой схемы 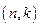- по­люсника при минимизации и преобразова­ний описывающих его функций необходимо стремиться к тому, чтобы в выражениях функций по одним выходам максимально ис­пользовались выражения функций (или их час­тей) по другим вы­ходам. Рассмотрим пример синтеза схемы 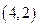- полюс­ника, заданного следующей таблицей [2]:

Входы	Выходы

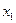
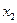
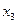
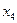
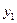
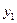
Дата добавления: 2014-11-29