I. Разработка алгоритмов. Графическое изображение (блок-схемы) и словесная запись алгоритмов

КАЗАНЬ – 2006

№1

ПРАКТИКУМ НА ЭВМ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАЧИ

ДЛЯ ПРОГРАММИРОВАНИЯ ПО ТЕМЕ:

«ОСНОВНЫЕ СТРУКТУРЫ УПРАВЛЕНИЯ»

Кугураков В.С., Самитов Р.К., Кугуракова В.В. Практикум на ЭВМ. Методические указания и задачи для программирования по теме: «Основные структуры управления». – Казань: КГУ, 2006. – 39 с.

Пособие предназначено для студентов, обучающихся по специальности «Прикладная математика и информатика» и направлению «Информационные технологии», а также для преподавателей, ведущих практические занятия по информатике, алгоритмическим языкам и программированию. Учебный материал представлен задачами для программирования, которые рекомендуется использовать при изучении темы «Основные структуры управления».

Ó Казанский государственный университет, 2006 г.

Ó Кугураков В.С., Самитов Р.К., Кугуракова В.В.

Для каждой из задач данного раздела требуется разработать алгоритм решения задачи. Следует рассмотреть различные способы записи алгоритмов. Используйте сначала блок-схемы – графический способ изображения алгоритмов. Разработайте соб­ственный язык (жаргон) для словесного описания алгоритмов "по шагам". Для проверки правильности составленного алгорит­ма следует строить (если это несложно) трассировочные табли­цы, "прокручивая" алгоритм на конкретных исходных данных и следя за изменением переменных. Хотя такими отладочными дей­ствиями нельзя доказать правильность алгоритма, они во мно­гих случаях позволяют выявить ошибки в алгоритме.

1. (Умножение натуральных чисел.) Вычислить n = m × k, используя операции сложения и а) вычитания; б) удваивания и деления пополам. (Операция div деления по­полам определена следующим образом: r div2 =s, если r= 2 s или 2 s+ 1.)

2. (Деление натуральных чисел.) Вычислить частное и ос­таток при делении m на n, используя операции сложения и вычитания.

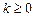3. (Возведение в степень.) Для заданных целых и вычислить , используя операции вычитания и умножения.

4. (Вычисление "показателя".) Для заданных целых m ³ 1 и n ³ 2 вычислить:

а) наименьшее целое k такое, что ;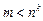

б) наибольшее целое k такое, что ;

в) количество цифр в десятичной записи числа m.

5. (Выделение квадрата.) Для заданного целого вычислить k – наибольшее целое, при котором m делится на k ² без остатка.

6. (Выделение показателя и степени.) Для заданных целых чисел m, 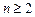вычислить наибольшее целое k, при котором m делится без остатка на: а) ;б) .

7. (Наибольший общий делитель.) Вычислить d = НОД(m, n) – наибольший общий делитель натуральных чисел m и n, используя следующие соотношения:

(1) если 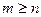, то НОД(m, n) = НОД(m–n, n);

(2) НОД(m, n) = НОД(n, m);

(3) НОД(n, 0) = n.

8. (Алгоритм Евклида.) В задаче 7 использовать вместо (1) следующее соотношение:

(1¢) если 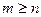, то НОД(m, n) = НОД(r, n), где r – остаток от деления m на п.

9. (Степенной алгоритм.)

а) Вычислить у = xⁿ ( – целое число), используя следующее соотношения (сведение задачи к меньшему значению n):

	если n четно,
если n нечетно,

где z = x ², – целая часть числа , x ⁰ = 1.

б) "Прокрутить" данный алгоритм для нескольких значений n и построить соответствующие трассировочные таблицы. Доказать правильность этого алгоритма и сравнить его с алгоритмом, полученным для задачи 3, оценивая (приближен­но) число используемых операций.

10. (Вычисление "основания".) Для заданных целых 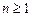и 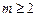, вычислить, используя алгоритм из задачи 9:

а) наименьшее натуральное k, при котором ;

б) наибольшее целое k, при котором .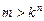

11. (Простое число.) Целое число , называется простым, если его натуральными делителями являются лишь 1 и само число p (в противном случае число p называется составным). Установить, является ли заданное число простым.

Указание: p – простое число тогда и только тогда, ког­да ни одно из целых чисел т, для которого , не является его делителем.

12. (Гипотеза Гольдбаха.) Согласно известной гипотезе любое четное число 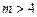представимо в виде суммы двух простых чисел. Установить, подтверждается ли эта гипотеза для заданного четного числа m.

13. (Эллиптическое сравнение.) Целые числа a и b называются сравнимыми по модулю n, если их остатки при делении на n совпадают. Этот факт обозначается как a º b (mod n). Для заданных целого и a, b Î Z_m = {0,1,..., 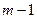} установить, имеет ли сравнение (mod m) хотя бы одно решение в целых числах x, y Î Z_m, причем , если b = 0.

14. (Проще, чем Большая Теорема Ферма.) Для заданных целых m, найти n – число решений сравнения (mod m) в целых числах x, y, z Î Z_m = {0,1,..., m– 1}, x y 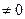. (Например, сравнение 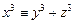(mod 5) имеет 20 решений, одно из них: x = 3, y = 1, z = 1.)

15. (Совершенные и дружественные числа.)

а) Натуральное число n называет­ся совершенным, если , где 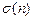– сумма дели­телей числа n. (Например, 6 – совершенное число, так как 12=1+2+3+6.) Вычислить, сколько имеется совершенных чисел £ 1000000.

б) Натуральные числа a и b называются дружественными, если . Найти все пары (a, b) дружественных чисел, для которых a + b < n, где n – заданное число.

16. (Теорема Лагранжа.) Всякое неотрица­тельное целое число можно представить в виде суммы четырех квадратов. (Например, 7=1²+1²+1²+2².) Однако для неко­торых чисел достаточно и меньшего числа квадратов. (Напри­мер, 4=2², 13=2²+3², 6=1²+1²+2².) Вычислить, сколько (минимально) квадратов требуется для указанного представ­ления заданного числа n.

17. (Гипотеза Эйлера.) Леонард Эйлер предполагал, что диафантово уравнение 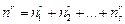не имеет решений в натуральных числах для любого показателя степени , если .

Опровергнуть данную гипотезу.

Подсказка. Попробуйте простым перебором найти решение уравнения 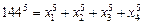. Решение сущствует! Попутно отметим, что имеется уникальный результат для s = 3, опровергающий гипотезу Эйлера:

422481⁴ = 414560⁴ + 217519⁴ + 95800⁴.

Дата добавления: 2014-11-29