Приклад розв’язання типових задач. Задача 1. Припустимо, що при 2% випадковому відборі у відібраних для обстеження 100 деталей встановлено

Задача 1. Припустимо, що при 2% випадковому відборі у відібраних для обстеження 100 деталей встановлено, що середня вага однієї деталі 2500г, дисперсія 900, зі 100 деталей 10 виявилися бракованими. З ймовірністю 0,954 встановити межі середньої ваги однієї деталі в генеральній сукупності, а з ймовірністю 0,997 — межі частки якісних деталей у генеральній сукупності.

Розв’язок

Граничну похибку Δх=tμ, визначаємо за формулою безповторного відбору. Чисельність генеральної сукупності

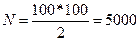шт.

За спеціальною таблицею знаходимо, що для ймовірності 0,954 t = 2, а для ймовірності 0,997 t =3. Таким чином,

г.

Звідси визначаємо довірчі межі генеральної середньої:

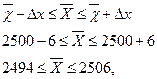
Тобто з ймовірністю 0,954 можна стверджувати, що середня вага однієї деталі в генеральній сукупності лежить в межах від 2494 до 2506г.

Аналогічно визначаємо межі для генеральної частки. Вибіркова частка якісних деталей ω = 90: 100 = 0,9.

Отже, гранична похибка частки

Генеральна частка W=w±Δw=w±tμ

Довірчі межі генеральної частки:

w-tμ≤W≤w+tμ

0,9-0,09≤ Р ≤0,9+0,09

0,81≤ Р ≤0,99

Отже, з ймовірністю 0.997 можна гарантувати, що частка якісних деталей у генеральній сукупності не виходить за межі від 81 до 99%.

Задача 2. Посівна площа під кукурудзою в селянських, спілках регіону становить 5000га. Посіви розташовані на 50 стогектарних ділянках. Для визначення врожайності способом серійної безповторної вибірки відібрано п'ять стогектарних ділянок, на яких здійснено суцільний облік зібраного врожаю кукурудзи:

Розв’язок

Показники урожайності кукурудзи

Номер ділянки	Середній урожай на ділянці, ц/га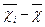
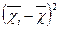
		-2
		-1
Разом

Визначимо середню урожайність на всіх ділянках:

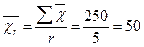ц/га

Між групова (міжсерійна) дисперсія

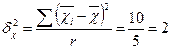
Тоді гранична помилка серійної вибірки при ймовірності Р=0,954:

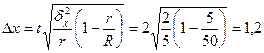ц/га

Звідси

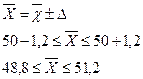
Отже, з ймовірністю 0,954 можна стверджувати, що середня врожайність кукурудзи в цілому регіоні коливається в межах від 48,8 до 5і,2 ц/га.

Задача3. Припустимо, що для господарства, в якому є 8000 корів, необхідно організувати: вибіркове обстеження з метою встановлення середньої річної молочної продуктивності корів. Якою має бути чисельність вибірки?

Розв’язок

Якщо орієнтуватися на повторний відбір, то в разі граничної похибки 30кг, ймовірності Р=0,954 і середнього квадратичного відхилення 300кг, визначеного за результатами аналогічних обстежень, необхідна чисельність вибірки становитиме:

корів

При без повторному відборі за тих самих умов необхідна чисельність вибірки становитиме:

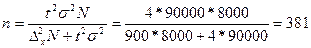корів

Цей розрахунок підтверджує, що за тих самих умов обсяг вибірки при безповторному відборі завжди менший, ніж при повторному.

Частку породних корів з похибкою до 5% за ймовірності 0,954 і дисперсії альтернативної ознаки 0,25 знаходимо необхідну чисельність вибірки:

- при повторному відборі:

- при без повторному відборі:

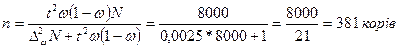
Отже, забезпечити очікувану точність при повторному відборі можна, досліджуючи 400 корів, а при без повторному відборі — 381.

Тема 12. ПОДАННЯ СТАТИСТИЧНИХ ДАНИХ: ТАБЛИЦІ, ГРАФІКИ, КАРТИ

Методичні поради до вивчення теми:

Метою вивчення теми є набуття вмінь подання статистичної інформації у формі таблиць, графіків, карт.

Найбільш раціональною формою подання статистичних даних є статистичні таблиці. Студентам слід звернути увагу на те, що статистичну таблицю можна порівняти з реченням: вона складається з підмета і присудка. Статистичним підметом є те, про що йдеться в таблиці. Статистичним присудком є числові підсумки, які харак­теризують статистичний підмет.

При вивченні теми статистичну таблицю необхідно розглядати як комбінацію горизонтальних рядків і вертикальних граф, перетин яких утворює клітини таблиці. Ліві, бічні і верхні клітини призначені для заголовків, а решта - для цифрових даних. Загальний заголовок розмішується над таблицею і виражає стисло її зміст. Розташовані зліва бічні заголовки розкривають зміст рядків підмета, а верхні – зміст граф (статистичного присудка) (рис. 12.1.).

№ з/п	Внутрішній заголовок, що розкриває зміст підмету	Верхні внутрішні заголовки, що розкривають зміст граф присудку
1
2	Бічні внутрішні заголовки, що розкривають зміст окремих рядків	Числові показники (присудок)
…
8
	Підсумок

Рис. 12.1. Схема статистичної таблиці

Студентам слід розглянути класифікацію видів статистичних таблиць за побудовою підмета (прості, групові, комбінаційні), за метою дослідження та призначенням (описово-інформаційні, аналітичні, типологічні, спеціального призначення) та запам’ятати основні правила складання та оформлення статистичних таблиць, зокрема:

1. Назва таблиці, заголовки рядків та граф повинні бути чіткими, лаконічними, без скорочень і зайвої та другорядної інформації.

2. У назві таблиці вказується її порядковий номер, об'єкт дослідження, його часова та географічна ознаки. Якщо назви окремих граф чи рядків повторяються, то їх доцільно об'єднати спільним заголовком.

3. У верхніх і бічних заголовках вказуються одиниці вимірювання з використанням загальноприйнятих скорочень (грн., т, м тощо). Якщо одиниця вимірювання спільна для всіх даних таблиці, її вказують у назві таблиці.

4. Для складних за побудовою таблиць графи доцільно ну­мерувати: графу з назвою підмета позначають літерою алфавіту, а інші графи - цифрами.

5. Узагальнена інформація граф таблиці міститься у підсу­мковому рядку з позначкою «Разом» (проміжний підсу­мок), «Всього» (остаточний підсумок), «В середньому». Підсумковий рядок може знаходитись на початку таблиці.

6. Значення показників у клітинах таблиці слід округляти у межах одного рядка чи графи з однаковим ступенем то­чності (до цілих; 0,1; 0,01 і т.д.).

7. Якщо немає відомостей про будь-який показник, ста­виться три крапки (...). Відсутність будь-якої ознаки в таблиці позначається тире (-). У тих випадках, коли клітина таблиці не підлягає заповненню, або бракує осмислення змісту, ставлять знак (х). Дуже малі числа записуються (0,0) або (0,00).

8. До таблиці у разі потреби додають примітки, в яких вка­зують джерела даних, дають докладне тлумачення змісту окремих показників та інші пояснення. Давати пояснення доцільно в тих випадках, якщо наведені дані вирізняються певними особливостями, наприклад, є попередніми, стосуються лише частини певної території, не охоплюють усіх одиниць сукупності тощо.

Для характеристики зміни показників у часі й просторі, вивчення структури та структурних зрушень, контролю за виконанням планових завдань, характеристики розміщення і поширення явищ у просторі, а також для аналізу зв'язків і залежностей між різними показниками або між значеннями варіаційної ознаки і частотами використовують статистичні графіки. Студентам необхідно знати такі основні елементи статистичного графіка, як: поле графіка, графічні образи, масштабні орієнтири та експлікація графіка.

При вивченні теми необхідно засвоїти такі основні правила побудови статистичних графіків:

1. Назва графіка має зрозуміло, чітко і стисло розкривати основний його зміст і відповідати на три запитання – «що?», «коли?», «де?».

2. При побудові графіка масштаб має бути таким, аби ясно і чітко проявлялися відмінності зображення статистичних величин і можна було їх легко порівнювати між собою.

3. На кожній масштабній шкалі графіка необхідно вказувати відповідні статистичні величини та одиниці їх вимірювання.

4. На осі ординат графіка має бути нульова точка. У випадках, коли мінімальне значення ознаки набагато вище нуля, доцільно робити розрив вертикальної шкали.

5. У статистичних графіках можна використовувати такі геометричні знаки, як крапки, відрізки прямих ліній, квадрати, прямокутники, кола, півкола, сектори, а також негеометричні знаки-символи у вигляді силуетів або малюнків.

6. Пояснювальні написи до окремих елементів графічного образу можуть лежати в полі графіка або виноситись як умовні позначенні за його межі.

Слід звернути увагу на класифікацію графіків за загальним призначенням (аналітичні, ілюстративні, інформаційні), за функціонально-цільовим призначенням (графіки групувань, рядів розподілу, динаміки, взаємозв'язку, порівняння), за формою графічних образів (крапкові, лінійні, площинні, просторові, фігурні), за типом системи координат (графіки у прямокутній та полярній системах координат), за масштабними шкалами (графіки з рівномірними, з функціональними, із змішаними шкалами), за виглядом поля графіків (діаграми, статистичні карти) тощо.

Лінійні графіки дуже поширені для характеристики зміни явищ в часі. При їх побудові на осі абсцис відкладають періоди часу, а на осі ординат – рівні динамічного ряду. Лінійні графіки будують і в тих випадках, коли необхідно порівняти динаміку різних показників, або однакових показників різних країн, підприємств.

Стовпчикові діаграми є графічним зображенням статистичних даних у вигляді стовпчиків (прямокутників). Їх використовують для наглядного зображення об’ємних явищ що вивчаються в часі і просторі і для зображення структури сукупності. Якщо основи стовпчиків розмістилися по осі ординат, а значення рівнів показника по осі абсцис, то одержимо стрічкові (полосові) діаграми.

Секторні діаграми представляють коло, розділене на сектори і використовуються в основному для зображення структури сукупності. Площа всього кола приймається за 100%, площа кожного сектора характеризує частину цілого і відповідає питомій вазі цієї частини в цілому. Секторні діаграми виразні в тому випадку, коли сукупність ділиться на більше, ніж на 4-5 частин і видні структурні зрушення, в іншому випадку використовують стрічкову діаграму.

У фігурних діаграмах в якості графічного образу використовують зображення самих предметів або різної кількості одного розміру або різного розміру але однієї кількості.

Знаки Варзара запропоновані російським статистиком Варзаром. Використовують їх коли необхідно порівняти величини, що представляють собою добуток двох співмножників і щоб показати роль кожного із них в формуванні цієї величини.

Картограми і картодіаграми використовують для зображення розподілу тих чи інших явищ по теорії. Картограма представляє собою схематичну географічну карту, на якій розподіл зображуваних явищ по території дається шляхом різної штриховки, або іншого кольору. Згущення штриховки або кольору свідчить про збільшення розміру показника. Картограми використовуються для зображення відносних величин інтенсивності і середніх величин. Але вони дають лише загальне поняття про кількісні відмінності показників по території, не показуючи їх абсолютних значень. На картодіаграмах розподіл показників по території дається на схематичній карті в формі стовпчиків, трикутників і т.д.

Студентам слід навчитися правильно будувати статистичні графіки та проводити інтерпретацію їх виду та форми. Використання програмних продуктів для побудови таблиць і графіків студенти мають опанувати в межах самостійної роботи.

Рекомендована література за темою

Основна [2, 13, 18, 23]

Додаткова [7, 15, 20, 21, 27, ]

Термінологічний словник

Діаграми – це вид графіків, в яких цифровим (кількісним) даним відповідають різні геометричні фігури і лінії.

Графічний образ – це сукупність різноманітних геометричних та графічних знаків, за допомогою яких відображують статистичні величини.

Експлікація графіка – це пояснення, що розкривають його зміст і основні елементи: заголовок (назва) графіка, одиниці виміру, умовні позначення.

Картограма – це схематична географічна карта, на якій розподіл зображуваних явищ по території подається за допомогою відповідних графічних і тонових символів (штриховки, крапки тощо).

Картодіаграма – це схематична географічна карта, поєднана з діаграмою, що дає можливість вивчення географічного розподілу досліджуваного явища.

Масштаб – це умовна міра переведення числового значення ста­тистичного явища в графічне і навпаки (це довжина відрізка шкали, прийнята за числову одиницю).

Масштабна шкала – це лінія, поділена на відрізки точками відповідно до прийнятого масштабу.

Масштабні знаки – це еталони, які зображають на графіку статистичні величини у вигляді квадратів, кругів, силуетів тощо.

Підмет статистичної таблиці – це статистична сукупність або її частина, яка характеризується числовими показниками (об’єкт вивчення).

Поле графіка – це простір, на якому розташовуються геометричні та інші знаки, тобто графічне зображення. Цей простір має певний розмір і обмежується або аркушем чистого паперу, або географічною чи контурною картою.

Присудок статистичної таблиці – це та частина, що вміщає показники, що характеризують досліджувану сукупність та її частини.

Статистичний графік – це масштабне зображення статистичних даних за допомогою ліній, геометричних фігур, малюнків або схематичних географічних карт.

Статистична таблиця – це форма найбільш раціонального, наочного і систематизованого викладу числових результатів зведення і обробки статистичних матеріалів.

Центрограма – це контурна карта, на якій розмішують короткі цифрові таблиці з інформацією про історико-географічний розвиток і розташування досліджуваного явища чи процесу.

Дата добавления: 2014-11-29