
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Задача 1. Зависимость пройденного телом пути от времени выражается уравнением (
|
|
|
|
Задача 1. Зависимость пройденного телом пути 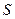 от времени
от времени 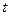 выражается уравнением
выражается уравнением 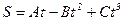 (
(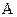 = 2 м/с,
= 2 м/с, 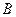 = 3 м/с2,
= 3 м/с2, 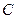 = 5 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени
= 5 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени 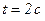 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
Дано:
 ; ;
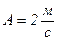 ; ;
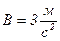 ; ;
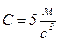 ; ;
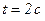 . .
| Решение:
Для определения зависимости скорости движения тела от времени определяем первую производную от пути по времени:
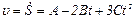 ,
или после подстановки ,
или после подстановки
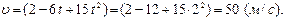 Для определения зависимости ускорения движения тела от времени определяем первую производную от скорости по времени: Для определения зависимости ускорения движения тела от времени определяем первую производную от скорости по времени:
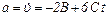 ,
или послеподстановки ,
или послеподстановки
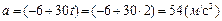 .
Пройденный путь определяется как разность .
Пройденный путь определяется как разность
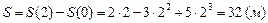 . .
|
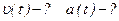 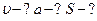
|
Ответ: 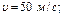
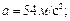
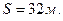
Задача 2. Тело брошено со скоростью 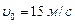 под углом
под углом 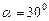 к горизонту. Принимая тело за материальную точку, определите нормальное
к горизонту. Принимая тело за материальную точку, определите нормальное 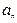 и тангенциальное
и тангенциальное 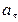 ускорение тела через 1,2 с после начала движения.
ускорение тела через 1,2 с после начала движения.
Дано:
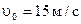 ; ;
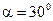 ; ;
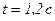 ; ;
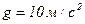 . .
| Решение
Построим чертеж и определим проекции
скорости 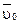 в начальный момент времени: в начальный момент времени:
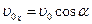 , , 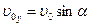 . .
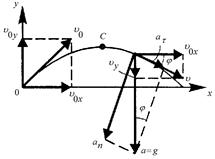
Рис.1.1 | ||
|
Проекция 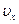 в процессе движения точки остается постоянной по величине и направлению.
в процессе движения точки остается постоянной по величине и направлению.
Проекция 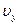 на ось
на ось 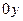 изменяется. В точке С (рис 1.1) скорость направлена горизонтально, т.е.
изменяется. В точке С (рис 1.1) скорость направлена горизонтально, т.е. 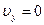 . Это означает, что
. Это означает, что 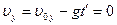 , где
, где 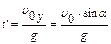 - время, в течение которого материальная точка поднимается до максимальной высоты, или после подстановки
- время, в течение которого материальная точка поднимается до максимальной высоты, или после подстановки 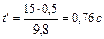 .
.
К моменту времени 1,2 с тело будет находиться на спуске. Полное ускорение в процессе движения направлено вертикально вниз и равно ускорению свободного падения 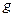 . Нормальное ускорение равно проекции ускорения свободного падения на направление радиуса кривизны, а тангенциальное ускорение - проекции ускорения свободного падения на направление скорости движения (см. рис.1.1).
. Нормальное ускорение равно проекции ускорения свободного падения на направление радиуса кривизны, а тангенциальное ускорение - проекции ускорения свободного падения на направление скорости движения (см. рис.1.1).
Из треугольников скоростей и ускорений имеем:
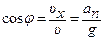 ,
, 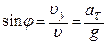 ,
,
откуда 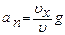 ,
, 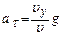 ,
,
где 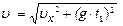 - скорость в момент времени
- скорость в момент времени 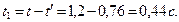
После подстановки получаем:
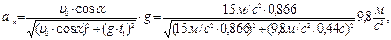
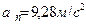 .
.
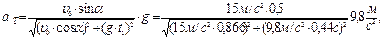
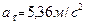 .
.
Ответ: 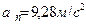 ,
, 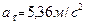 .
.
Задача 3. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Дано:
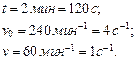
| Решение:
Запишем формулы для угла поворота и угловой скорости при равнозамедленном вращении:
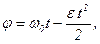 (1) (1)
|
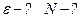
| 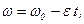 (2) (2)
|
где 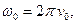
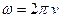 - угловые скорости в начальный и конечный моменты времени соответственно.
- угловые скорости в начальный и конечный моменты времени соответственно.
Из уравнения (2) получаем:
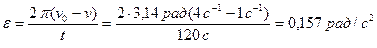 .
.
Угол поворота 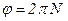 . Поэтому выражение (1) можно записать так:
. Поэтому выражение (1) можно записать так: 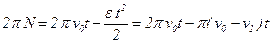 .
.
Отсюда: 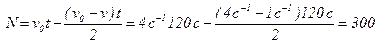 .
.
Ответ: 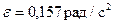 ;
; 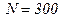 .
.
Задача 4. Точка движется по окружности радиусом 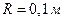 так, что зависимость угла поворота радиуса от времени дается уравнением
так, что зависимость угла поворота радиуса от времени дается уравнением 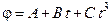 , где
, где 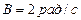 ,
, 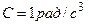 . Определите к концу второй секунды вращения: а) угловую скорость; б) линейную скорость; в) угловое ускорение; г) нормальное ускорение; д) тангенциальное ускорение.
. Определите к концу второй секунды вращения: а) угловую скорость; б) линейную скорость; в) угловое ускорение; г) нормальное ускорение; д) тангенциальное ускорение.
Дано:
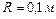 ; ; 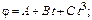 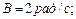 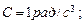 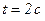 . .
| Решение:
Зависимость угловой скорости от времени определяем, взяв первую производную от угла поворота по времени, т.е.  .
Для момента времени .
Для момента времени  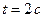
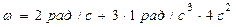 , , 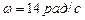 .
Линейная скорость точки .
Линейная скорость точки 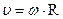 , или после подстановки , или после подстановки 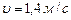 . .
|
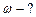 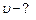
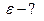 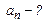 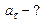
| |
Зависимость углового ускорения точки от времени определится первой производной от угловой скорости по времени, т.е. 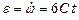 .
Для момента времени .
Для момента времени 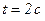 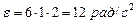 . Нормальное и тангенциальное ускорения определяются по формулам соответственно: . Нормальное и тангенциальное ускорения определяются по формулам соответственно:
| |
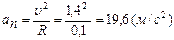 и
и 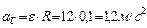 .
Ответ: .
Ответ: 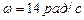 ; ; 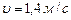 ; ; 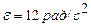 ; ;
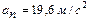 ; ; 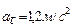 . .
|
Контрольные задания
1.1. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело: 1) за первую 0,1 с своего движения, 2) за последнюю 0,1 с своего движения? Считать 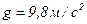 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.2. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый 1 м своего пути, 2) последний 1 м своего пути? Считать 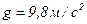 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.3. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пренебрегая сопротивлением воздуха, определите для момента времени 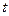 = 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории. Считать
= 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории. Считать 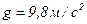 .
.
1.4. Камень брошен горизонтально со скоростью 5м/с. Определите нормальное и тангенциальное ускорения камня через 1 с после начала движения. Считать 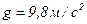 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.5. Материальная точка начинает двигаться по окружности радиусом 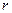 = 2,5 см с постоянным тангенциальным ускорением
= 2,5 см с постоянным тангенциальным ускорением 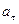 = 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения
= 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения 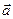 образует с вектором скорости
образует с вектором скорости 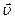 угол 45°; 2) путь, пройденный за это время движущейся точкой.
угол 45°; 2) путь, пройденный за это время движущейся точкой.
1.6. Зависимость пройденного телом пути от времени задаётся уравнением 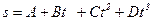 , где
, где 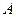 =0,1м,
=0,1м, 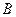 =0,1м/с,
=0,1м/с, 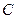 =0,14м/с2,
=0,14м/с2, 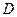 =0,01м/с3. 1) Через сколько времени после начала движения ускорение тела будет равно 1м/с2? 2) Чему равно среднее ускорение тела за этот промежуток времени?
=0,01м/с3. 1) Через сколько времени после начала движения ускорение тела будет равно 1м/с2? 2) Чему равно среднее ускорение тела за этот промежуток времени?
1.7. Зависимость пройденного телом пути от времени задаётся уравнением 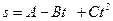 , где
, где 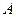 =5м,
=5м, 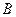 =4м/с,
=4м/с, 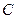 =1м/с2. Запишите выражения для скорости и ускорения. Определите для момента времени
=1м/с2. Запишите выражения для скорости и ускорения. Определите для момента времени 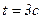 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
1.8. Зависимость пройденного телом пути 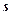 от времени
от времени 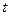 выражается уравнением
выражается уравнением 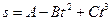 (
(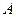 = 2 м/с,
= 2 м/с, 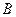 = 3 м/с2,
= 3 м/с2, 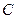 = 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени
= 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени 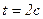 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
1.9. Нормальное ускорение точки, движущейся по окружности радиусом 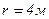 , задается уравнением
, задается уравнением 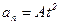 , где
, где 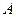 = 4 м/с4. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время
= 4 м/с4. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время 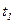 = 5 с после начала движения; 3) полное ускорение для момента времени
= 5 с после начала движения; 3) полное ускорение для момента времени 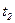 = 1 с.
= 1 с.
1.10. Кинематические уравнения движения двух материальных точек имеют вид 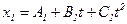 и
и 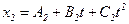 , где
, где 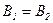 ,
, 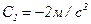 ,
, 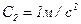 . Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения
. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения  и
и 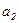 для этого момента.
для этого момента.
1.11. Диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 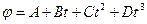 (
(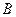 = 1 рад/с,
= 1 рад/с, 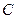 = 1 рад/с2,
= 1 рад/с2, 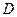 = 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения тангенциальное, нормальное и полное ускорения.
= 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения тангенциальное, нормальное и полное ускорения.
1.12. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 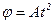 (
(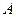 =0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
=0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
1.13. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 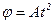 (
(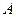 =0,1рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
=0,1рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
1.14. Диск радиусом 0,2 м вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением 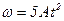 , где
, где 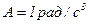 . Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения.
. Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения.
1.15. Диск радиусом 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением 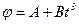 (
(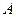 = 2 рад,
= 2 рад, 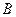 = 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
= 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
1.16. Якорь электродвигателя, имеющий частоту вращения 50 с-1, после выключения тока, сделав 628 оборотов, остановился. Определите угловое ускорение якоря.
1.17. Колесо автомобиля вращается равноускоренно. За время 2 мин оно изменило частоту вращения от 60 до 240 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
1.18. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найдите угловое ускорение колеса.
1.19. Колесо спустя 1 мин после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных колесом за эту минуту. Движение считать равноускоренным.
1.20. Колесо, вращаясь равнозамедленно, при торможении уменьшило частоту вращения за 1 мин с 300 об/мин до 180 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных за это время.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 6535; Нарушение авторских прав?; Мы поможем в написании вашей работы!