Методы и способы начисления процентов

В банковской практике существуют различные методы и способы начисления процентов.

Так, в банковской практике применяются простые и сложные проценты.

Простые проценты используются, прежде всего, при краткосрочном кредитовании, когда один раз в квартал или другой срок, определенный договором, производится начисление процентов и выплата их кредитору. Как правило, в настоящее время преимущественно применяется изложенный выше способ. Сумма выплачиваемых процентов (I) за период d рассчитывается по формуле:

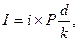
где P – сумма вклада (первоначальный долг);

i –размер процентов;

d – срок хранения вклада в днях;

k – количество дней в году.

Сумма вклада с процентами за хранение (S) рассчитывается по формуле:

S = Р + I;

Срок вклада в годах (n), срок вклада в днях (d) и годовая учетная ставка простых процентов (i) рассчитываются по формулам:

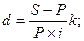
где S – наращенная с процентами сумма вклада;

Общий объем платежей заемщика с учетом основной суммы долга можно также рассчитать по следующей формуле:

S = Р(1 + ni),

где S – сумма выплат по кредиту с учетом первоначального долга;

Р– первоначальный долг;

i –ставка процентов;

n–продолжительность ссуды в годах, либо отношение периода пользования ссудой в днях к применяемой базе (360 или 365 дням).

Очень часто в банковской практике приходится производить операцию, обратную процедуре начисления процентов. Это имеет место, например, в случае обращения дисконтных векселей. В этом случае при определении первоначального долга будет применяться следующая формула:

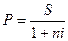
Предположим, банк выпустил вексель на следующих условиях: вексельная сумма по номиналу 100 млн. руб. сроком на 3 месяца при условии уплаты 120% годовых. Сумма платежа в случае размещения векселя (стоимость покупки) составит:

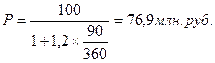
Особую важность в условиях высокого уровня инфляции приобретает определение реального дохода от депозитных (кредитных) вложений. Сумма вклада с процентами, пересчитанная с учетом инфляции (P_t) рассчитывается по формуле:

;

где t_r – уровень инфляции за срок хранения.

Уровень инфляции за срок хранения t_r рассчитывается следующим образом:

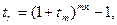
где mn – количество месяцев в сроке хранения;

t_m – месячный уровень инфляции.

Например, при условии, что размер вклада составил 100 тыс. руб. на срок 6 месяцев под 40 % годовых номинальный доход вкладчика составит:

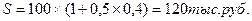
Однако, при условии, что среднемесячный уровень инфляции за период хранения составит 5 %, то сумма реального дохода (пересчитанная с учетом инфляции), который получит вкладчик составит:

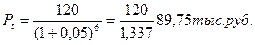
Таким образом, через полгода вкладчик получит 120 тыс. руб., покупательная способность которых составит 89750 руб.

В банковской практике возможно использование сложного процента, как правило, при долгосрочном кредитовании, когда начисленные суммы не выплачиваются кредитору до окончания сделки, а увеличивают основную сумму долга. При использовании этого метода размер начисленных средств включается в задолженность и на них продолжает начисляться процент (т.е. проценты начисляются на проценты). Формулу для начисления сложных процентов и определения общей суммы задолженности можно представить в виде:

Наращенная сумма вклада с процентами рассчитывается по следующей формуле:

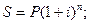
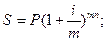
где S – наращенная сумма вклада с процентами;

n – срок хранения вклада в годах;

m – количество периодов начисления в году;

mn – количество периодов начисления за срок хранения.

Сумма начисленных процентов рассчитывается по формуле:

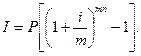
Рассмотрим условный пример.

Допустим, вкладчик планирует положить в банк на депозит 200 тыс. руб. сроком на 10 месяцев. При этом предлагаются следующие условия хранения:

банк начисляет на вклады 70 % годовых по простой процентной ставке;

банк начисляет проценты на вклады ежемесячно по сложной ставке 60 % годовых (начисленные после первого периода начисления проценты не выплачиваются, а присоединяются к сумме вклада).

Рассчитаем наращенную сумму вклада с процентами по 2-м вариантам:

1.

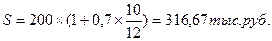
2.

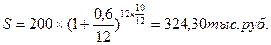
Таким образом, несмотря на то, что при начислении по простой процентной ставке проценты, начисляемые банком по вкладам, выше (70 % годовых), чем при начислении по сложной процентной ставке (60 % годовых), доход, получаемый вкладчиком при существующих условиях будет больше при использовании второго варианта хранения.

Такие же методы начисления процентов могут использоваться при кредитовании банком своих клиентов. При этом банк должен тщательно анализировать все моменты, которые могут в конечном итоге повлиять на прибыльность банковских операций. Например, необходимо учитывать характер инфляции и в этой связи определять, что целесообразней для банка: либо наращивать сумму долга посредством начисленных, но невостребованных процентов, либо получать ежегодную плату за кредит.

Возможны различные способы начисления процента: они определяются характером измерения количества дней пользования ссудой и продолжительностью года в днях (временной базы для расчета процентов). Так, число дней ссуды может определяться точно или приближенно, когда продолжительность любого полного месяца признается равной 30 дням. Временная база приравнивается либо к фактической продолжительности года (365 или 366 дней) или приближенно к 360 дням. Соответственно, применяют следующие варианты начисления сложных процентов:

1. Точные проценты с фактическим числом дней ссуды; этот способ дает самые точные результаты и применяется многими центральными и крупными коммерческими банками. Он характеризуется тем, что для расчета используется точное число дней ссуды, временная база равняется фактической продолжительности года. Например,

Р – сумма выданного кредита – 100000 руб.,

i – ставка процента – 9% годовых.

K – точное число дней ссуды,

S – наращенная сумма долга.

Тогда, S = 100000 x (1 + 0,09% x 260 дн.: 365 дн.) = 106411 руб.

2. Обыкновенные проценты с точным числом дней ссуды. В этом случае также как и в предыдущем, для расчета берется точное число дней ссуды, но временная база приравнивается к 360 дням. Если срок кредита превышает 360 дней, то сумма начисленных процентов будет больше, чем предусмотрено годовой ставкой (так, если период ссуды равен 364 дням, то 364:360 = 1,011). Рассмотрим данный способ на предложенном выше примере:

S₂ = 100000 x (1 + 0,09% x 260 дн.: 360 дн.) = 106499 руб.

3. Обыкновенные проценты с приближенным числом дней ссуды. Здесь продолжительность ссуды в днях определяется приближенно, временная база равна 360 дням. Считается, что точное число дней ссуды в большинстве случаев больше приближенного, поэтому и размер начисленных процентов с точным числом дней обычно больше, чем с приближенным.

В нашем примере приближенное число дней ссуды равно 257 дням (S₃), учитывая это:

S₃ = 10000 x (1 + 0,09% x 257 дн.: 360 дн.) = 106424 руб.

Практика показывает, что второй способ начисления процентов, а именно, обыкновенные проценты с точным числом дней ссуды дает несколько больший результат относительно двух других вариантов, что необходимо иметь ввиду кредитору при оформлении ссуды.

Глава 12. Финансовый рынок

Дата добавления: 2014-11-29