Исторический аспект

Системы счисления.

Элементы информационных технологий

Под системой счисления понимается способ записи чисел с помощью цифр и символов (букв).

Исторически человечество наряду с созданием письменности разрабатывало также и способы записи чисел, требуемых для хранения данных о количестве предметов. В этом случае появляется возможность сравнивать количества различных множеств объектов.

Самой древней, пожалуй, системой счисления, является так называемая унарная система (или счетно-импульсная). Унарная система является однородной и непозиционной. Число в этой системе строится прибавлением единственного знака к предыдущему такому же числу:

I II III IIII IIIII IIIIII IIIIIII

Система позволяет представить любое, сколь угодно большое число. Однако представление чисел крайне неэффективно с точки зрения компактности.

Следующим этапом в развитии систем счисления является римская система. Она также относится к непозиционным системам. В римской системе сохраняются некоторые элементы унарной системы и в то же время предпринимаются меры к более компактному представлению числа путем замены совокупности элементарных цифр на определенные символы (иероглифы).

I II III IV V VI VII VIII IX X XI XII XIII XIV XV XVI XVII

Таким образом, в этой системе латинские буквы соответствуют следующим количествам:

L – 50, C – 100, D – 500, M – 1000

Например:

2007 – MMVII, 444 – CDXLIV.

В этой системе очень трудно выполнять арифметические операции.

Дальнейшее развитие представления чисел привело к распространению позиционных систем счисления, в которых значение ("вес") цифры зависит от ее положения в числе.

Первой известной позиционной системой счисления была шестидесятеричная система у древних вавилонян, использующая клинопись. Так, число 32 они записывали: <<<VV, а число 92: V<<<VV.

Таким образом, основанием системой счисления называется количество цифр (назовем его q). Величина q показывает, во сколько раз возрастает вес цифры, если ее переместить в следующий разряд числа. Отметим, что данная система требует наличия цифры ноль.

Позиционная система является однородной в смысле применения правил построения числа независимо от места расположения текущей цифры.

Именно однородность позволяет конечным числом знаков (в десятичной системе – 10) выразить бесконечное количество чисел.

Рассмотрим более подробно десятичную систему счислению.

Она имеет 10 цифр: 0,1,2,3,4,5,6,7,8,9.

Например, число 111.

Вес цифры изменяется в 10 раз: 100+10+1 = 111.

Поэтому в позиционной системе счисления любое число можно представить в виде следующего выражения:

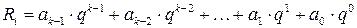
Таким же образом можно представить и дробное число:

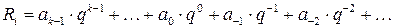
Например, число 16,37 можно представить в виде:

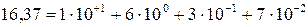
Дата добавления: 2014-11-29