Перевод чисел из одной системы счисления в другую

A, B, C, D, E, F.

0, 1, 2, 3, 4, 5, 6, 7.

Восьмеричная и 16-ричная система счисления.

Арифметические операции в двоичной системе счисления.

Рассмотрим теперь арифметические действия в двоичной системе счисления. Для их выполнения приведем таблицы сложения и умножения:

Таблица сложения
1 операнд
2 операнд
Результат

Таблица умножения
1 операнд
2 операнд
Результат

Хотя в двоичной системе можно выразить любые, сколь угодно большие числа, в компьютере количество разрядов, необходимых для представления чисел, ограничено. Поэтому при выполнении арифметических операций необходимо следить за величиной чисел, участвующих в вычислениях, не допуская переполнения разрядной сетки.

Большинство арифметических операций выполняются в двоичной системе счисления так же, как в 10-тичной.

Примеры арифметических действий.

Сложение:

	1 0 0 1 0 0 1 1	-
+
	0 1 0 1 1 1 1 0	-
	------------------		----
	1 1 1 1 0 0 0 1	-

Вычитание

	1 0 0 1 0 0 1 1	-
-
	0 1 0 1 1 1 1 0	-
	------------------		----
	0 0 1 1 0 1 0 1	-

Умножение

	0 0 0 1 1 0 1	-
*
	0 0 0 0 1 0 1	-
	------------------		----
	1 0 0 0 0 0 1	-

Большая длина двоичных чисел неудобна для их чтения и названия. Поэтому для того, чтобы удобнее было оперировать с двоичными кодами, используют восьмеричную и шестнадцатеричную системы счисления. Особенность их состоит в том, что основания этих систем кратно двум:

2³ = 8; (1.4.a)

2⁴ = 16; (1.4.b)

Восьмеричная система с основанием q = 8 имеет цифры:

16-ричная система с основанием q = 16 имеет цифры:

Как известно, в реальной практике все числовые данные представлены в десятичной системе счисления. Однако компьютерные системы работают в двоичной системе счисления. Поэтому возникает необходимость перевода чисел. Значения чисел при этом не меняются, изменяется только форма представления.

Входные данные из входного потока поступают в десятичном виде, затем переводятся в двоичный вид, в котором и выполняются все вычисления и преобразования данных, результаты затем переводятся в десятичный вид для вывода на печать или монитор.

Рис. 1.1.5.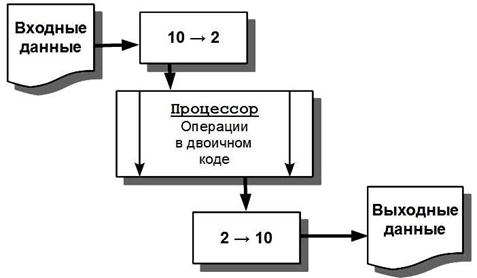

Восьмеричная и 16-тиричная системы счисления используются для индикации, документирования, программирования и отладки программ, для представления в удобном виде длинных двоичных наборов данных.

Определим правила переводы чисел из одной системы в другую. Для выполнения перевода нам будет нужна следующая таблица:

Таблица 1.1.5.

10-тичное число	2-ичное число	8-ричное число	16-ричное число	2^х
			A
			B
			C
			D
			E
			F

1) Перевод 2 → 10.

Для перевода необходимо двоичное число представить в виде выражения по степеням основания и вычислить это выражение в десятичной системе счисления. Например:

2) Перевод 10 → 2.

Для перевода необходимо десятичное число циклически делить на основание новой системы (q=2) до тех пор, пока частное не станет равным нулю. Остатки, полученные в операциях деления, начиная с последнего, представляют собой изображение двоичного числа. Например:

147 | 2

146 73 | 2

1 72 36 | 2

1 36 18 | 2

0 18 9 | 2

0 8 4 | 2

1 4 2 | 2

0 2 1 | 2

0 0 0

= 10010011₂

3) Перевод 8 → 10.

Для перевода необходимо восьмеричное число представить в виде выражения по степеням основания q=8 и вычислить это выражение в десятичной системе счисления. Например:

4) Перевод 10 → 8.

Для перевода необходимо десятичное число циклически делить на основание новой системы (q=8) до тех пор, пока частное не станет равным нулю. Остатки, полученные в операциях деления, начиная с последнего, представляют собой изображение двоичного числа. Например:

147 | 8

144 18 | 8

3 16 2 | 8

2 0 0

= 223₈

5) Перевод 2 → 8.

Пользуясь свойством (1.4.a), для перевода необходимо двоичное число разделить условно на триады (по три разряда), начиная с младшего разряда, а затем каждую триаду представить в виде восьмеричной цифры из таблицы 1.5.1. Например:

10.011.101.110.0012 = 23561₈

6) Перевод 8 → 2.

Пользуясь свойством (1.4.a), для перевода необходимо каждую цифру восьмеричного числа представить в виде соответствующей триады двоичного числа из табл. 1.5.1.

Например:

27453₈ = 10.111.100.101.011

7) Перевод 16 → 2 и 2 → 16.

Пользуясь свойством (1.4.b), перевод выполняется аналогично 5) и 6), но 16-тиричное число в этом случае должно быть представлено в виде соответствующей тетрады двоичного числа, взятой из табл. 1.1.5. Например:

2FC8E₁₆ = 10.1111.1100.1000.11102

Дата добавления: 2014-11-29