Комбинаторные меры информации

Комбинаторная мера основана на комбинировании объектов. Образование комбинаций есть одна из форм кодирования информации, и количество ее определяется как количество комбинаций элементов.

Комбинирование возможно группированием неодинаковых элементов, изменением позиции элемента в данной комбинации, изменением количества элементов и т.д. В комбинаторике рассматриваются различные виды соединений элементов. Рассмотрим их подробнее.

1. Сочетания из "n" элементов по "m",

различающиеся только составом элементов. Количество комбинаций: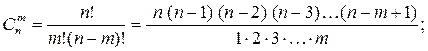

Пример. Cоставить сочетания:

а) из 3-х элементов {A,B,C} по 2. Имеем: AB, BC, AC. Всего 3 комбинации.

б) из 4-х элементов {A,B,C,D} по 2. Имеем: AB, AC, AD, BC, BD, CD. Всего 6 комбинаций.

2. Перестановки из "N" элементов, различаются только их порядком в комбинации. ;

Пример. Составить перестановки из 3-х элементов. Всего 3!=1*2*3=6.

Имеем следующие комбинации: ABC, ACB, BAC, BCA, CAB, CBA.

3. Размещения из "n" элементов по "m", различаются и составом элементов и их порядком. ;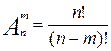

Пример. Составить размещения из 4-х элементов по 2. Всего можно составить 12 комбинаций.

Имеем следующие комбинации:

AB, AC, AD, BC, BD, CD,

BA, CA, DA, CB, DB, DC.

4. Размещения с повторениями отличаются тем, что элементы в комбинации могут повторяться. ;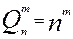

Количество информации при комбинировании элементов многократно возрастает. Так, в случае сочетаний из 10 элементов по 0,1,2,3,…9 элементов имеем общее число комбинаций:

=

= 1+10+45+120+210+120+45+10+1=1024;

Перестановки тех же 10 элементов дают:

;

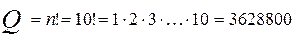Размещения с повторениями из 10 элементов по 10 приводят к еще большему числу комбинаций:

;

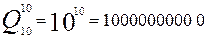Дата добавления: 2014-11-29