Статистические меры информации

Недостатком структурного метода измерения информации является то, что в нем не учитывается вероятность наступления того или иного исхода. Для определения количества информации в случае, если исходы опыта имеют разную вероятность, используется статистическая мера К.Шеннона, предложенная им в 1948 году.

В основе статистического метода определения информации лежит положение о том, что получение информации снимает часть некоторой (априорной, до опытной) неопределенности.

Большинство источников информации характеризуется неопределенностью, связанной с неодинаковой вероятностью происходящих событий. Естественно, что с ростом числа возможных исходов неопределенность должна возрастать. Меру степени неопределенности называют энтропией.

Пусть мы имеем опыт, имеющий "N" равновероятных исходов.

Такую неопределенность называют равной:

;

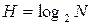Это выражение можно записать в виде:

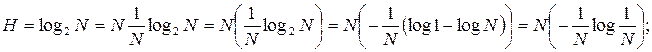Из теории вероятностей известно, что 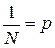- вероятность любого из N возможных исходов опыта, поэтому выражение (1) переписываем в виде:

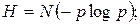
При N=2 имеем:

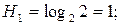(бит))

Бит - это единица для измерения степени неопределенности опыта.

А как же измерить неопределенность в случае разновероятных исходов?

Пусть некоторый опыт характеризуется следующей таблицей вероятности:

Исходы опыта: A₁ A₂ A₃... A_i... A_N

Вероятность: p₁ p₂ p₃... p_i... p_N

Естественно, что p₁ + p₂ + p₃ +... + p_i + p_N = 1.

Тогда в соответствии с формулой (2) меру неопределенности этого опыта запишем в виде:

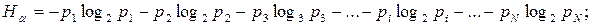
или

(1.2.5)

Полученное выражение имеет вид, совпадающий с видом выражения для энтропии в статистической физике, причем это несет не только формальный, но и содержательный характер.

Поэтому величину 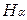называют энтропией опыта a.

Свойства выражения (1.2.5): Любое слагаемое всегда положительно, т.к. 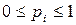, а следовательно 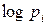всегда отрицателен. При 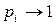выражение 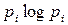убывает и стремиться к 0, т.к. .

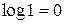Пример. Пусть мы имеем следующий опыт: к нам пришло следующее сообщение: А₁ А₃ А₁ А₃ А₃ А₂ А₃А₄

Требуется определить количество информации в данном сообщении.

Алфавит этого сообщения состоит из 4 букв: А₁, А₂, А₃, А₄.

Следовательно, для кодирования этих букв достаточно будет двух двоичных разрядов: А₁ – 00, А₂ ­– 01, А₃ – 10, А₄ – 11.

Если применить меру Хартли, то для передачи данного сообщения при применении равномерного кода необходимо будет 16 двоичных разрядов, т.е. 16 бит. Причем на одну букву приходится 2 бита: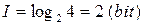

Однако такой подход не учитывает неравной вероятности появления букв в сообщении и поэтому не может считаться правильным.

Определим вероятности появления букв в сообщении:

P₁ = 0,25; P₂ = 0,125; P₃ = 0,5; P₄ = 0,125;

В этом случае количество информации, приходящейся на одну букву в этом сообщении, равно:

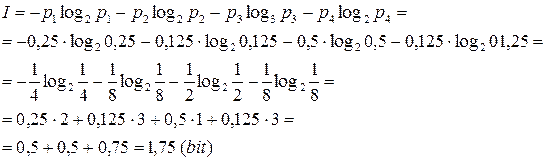
И таким образом, общие количество информации в этом сообщении составляет 8*1,75 = 14 (bit), что меньше, чем при равномерном коде.

Отсюда следует, что неравная вероятность появления букв в сообщении приводит к уменьшению избыточности количества информации.

В том же 1948 году К.Шеннон (на фото) доказал теорему о том, что возможен такой способ кодирования, который приводит к уменьшению длины двоичного кода сообщения, в котором наблюдается неравная вероятность появления букв. Тогда же он совместно с Фано предложил алгоритм оптимального кодирования, позволяющий уменьшать длину сообщения. Этот алгоритм широко применяется в программах архивирования данных.

Мера Шеннона и алгоритмы, разработанные им для кодирования информации, широко применяются в практике программирования, в частности, при разработке алгоритмов архивации файлов, например таких, как pkzip, arj, zip, 7zip, rar и ряда других, а также в системах обнаружения и исправления ошибок при передаче данных.

Дата добавления: 2014-11-29