Лабораторна робота №15

Розв’язування задач математичного аналізу засобами табличного процесора MS Excel.

Мета роботи: навчитися розв`язувати задачі математичного аналізу, використовуючи інструменти табличного процесора MS Excel.

Теоретичний матеріал: повторити поняття похідної, геометричний зміст похідної, побудова діаграм в MS Exсel, методи обчислення інтегралів: метод прямокутників та метод трапецій, числова послідовність, числові ряди, діалогове вікно Прогрессия, ряди Фурье, процедура Анализ Фурье, Пакет анализа.

ЗАВДАННЯ ДО РОБОТИ:

1. Найти производную функции y = sin x на промежутке х 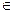[0; 6,2] при шаге дискретизации х = 0,2. Построить график функции и её производной.

o Для решения задачи заполняем таблицу начальных данных:

o Вводим в ячейку А5 – Аргумент. В ячейку А6 первое значение аргумента – 0 (левую границу диапазона). Далее в ячейку А7 введём второе значение: левая граница плюс шаг дискретизации =A6+$C$3. Теперь необходимо скопировать формулу в ячейки А8:А37. Значения аргумента введены.

o Далее требуется ввести значения функции (в примере синуса). В ячейку В5 вводим слово С инус. В ячейке В6 должно находится значение синуса, соответствующее значению аргумента в ячейке А6. Для этого открываем окно Мастер функций, и, среди математических функций выбираем SIN. Указываем значение аргумента синуса щелчком мыши на ячейке А6. Нажимаем ОК. В ячейке В6 появляется 0. Теперь необходимо скопировать функцию из ячейки В6 в ячейки В7:В37. Значения синуса получены.

o Теперь по введенным в рабочую таблицу данным необходимо найти значения производной. Для этого в ячейку С5 вводим слово Производная. В ячейку С7 вводим формулу дифференцирования, согласно трёхточечной формулы численного дифференцирования =(B8-B6)/($D$3*$C$3). Копируем её до ячейки С37. Получены значения производной.

o Далее по полученным данным строим диаграмму. В диалоговом окне Мастер диаграмм выбираем тип диаграммы – график, вид – левая верхняя. Во втором окне Мастера указываем диапазон данных – В6:С37. проверяем положение переключателя Ряды в: столбцах. Выбираем вкладку Ряд и вводим диапазон подписей оси Х: А6:А37. В третьем окне Мастера вводим подписи осей Х и У: Аргумент и Значения, соответственно, а также указываем название диаграммы. Появляется следующая диаграмма:

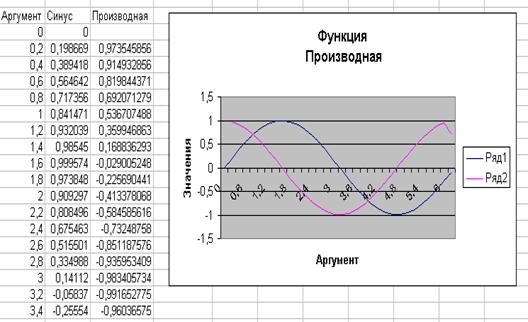Знайти похідну функції:

1. в точці .
2. в точці .
3. в точці .
4. в точці .
5. в точці .
6. в точці .
7. в точці .
8. в точці .
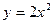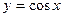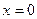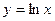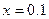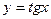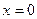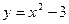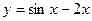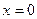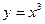9. 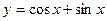в точці .
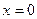10. 10. 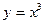+2х в точці х=1.

2.Обчислити визначений інтеграл засобами табличного процесора MS Excel.

2.1.Методом прямокутників обчислити 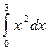з кроком .

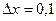Цей інтеграл може бути обчислений аналітично:

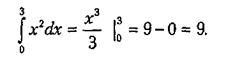
2.1.1.Для знаходження визначеного інтегралу методом прямокутників необхідно ввести значення підінтегральної функції 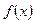в робочу область таблицю Ехсе1 в діапазоні 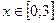з заданим кроком 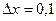. Заповнюємо таблицю Початкові дані.

2.1.2.Складаємо таблицю даних (х і 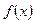). Нехай перший стовбець буде значення х, а другий 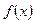. Для цього в комірку А6 вводимо слово Аргумент, а в комірку В6 — слово Функція. В комірку А7 вводимо перше значення аргументу – ліва границя діапазону (0). В комірку А8 вводимо наступне значення аргументу – ліва границя діапазону «+» крок побудови =A7+$D$4. Потім, використовуючи функцію Автозаполнение, отримуємо всі значення аргументу.

2.1.3.Далі вводимо значення підінтегральної функції. В комірку В7 записуємо вид підінтегральної функції: = A7^2. Натискаємо клавішу Enter. В комірці з’явиться 0. Тепер необхідно протабулювати функцію із В7 до комірки В37. Автозаповненням копіюємо цю формулу в діапазон В5:В35. В результаті отримали таблицю даних для знаходження інтегралу.

2.1.4.В комірку D38 вводимо формулу =$D$4 *, потім викликаємо Мастер функций. В діалоговому вікні Мастер функций –в полі Категория вибираємо Математические — функцію Сумм. Натискаємо кнопку ОК. З’являється діалогове вікно Аргументи функції. В робоче поле число 1 за допомогою миші вводимо діапазон комірок В7:В37.

Натискаємо кнопку ОК. В комірці D38 з’являється наближене значення шуканого інтегралу (9,455).

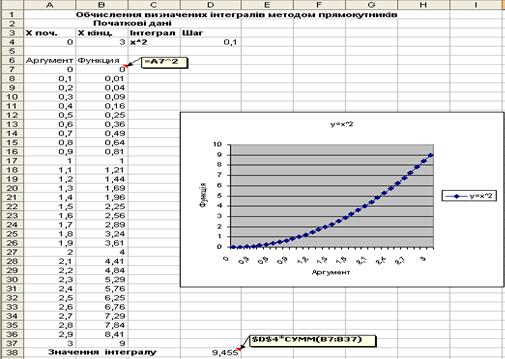
Порівнюючи отримане наближення з істинним значенням інтегралу, знайдене аналітично, можна побачити, що похибка наближення методу прямокутників, в даному випадку достатньо вагома – 0,455.

2.2.Методом трапецій обчислити інтеграл 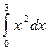з кроком .

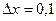Для знаходження визначеного інтегралу методом трапецій, значення підінтегральної функції 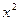повинні бути введені в робочу таблицю Excel в діапазоні 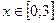із заданим шагом 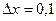. Тому ці етапи повністю аналогічні етапам попереднього розв’язку. Оскільки таблиця даних для знаходження інтегралу уже введена, переходимо відразу до наступного етапу.

Тепер в комірці D38 може бути знайдене наближене значення інтегралу за методом трапецій. Для цього, в комірку D38 вводимо формулу = $D$4*((B5+B35)/2+, потім викликаємо Мастер функций – функцію Сумм. У робочому полі діалогового вікна Аргументи функції. число 1 за допомогою миші вводимо діапазон комірок В8:В36. Натискаємо кнопку ОК і ще раз ОК. В комірці D38 з’явиться наближене значення шуканого інтегралу (9,005), а в рядку формул – формула = $D$4*((B7+B37)/2+СУММ(B8:B36)).

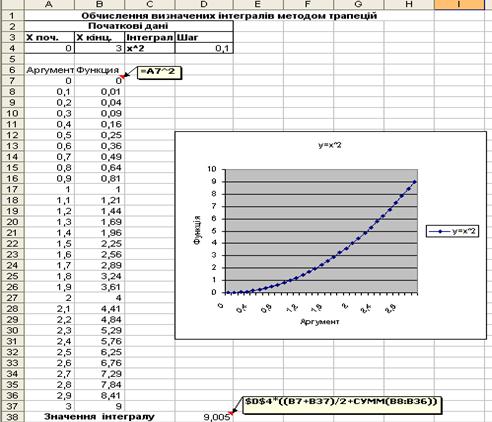
Отримуючи порівняне наближення з істинним значенням інтегралу, можна побачити, що похибка наближення методу трапецій в даному випадку незначна – 0,005.

2.3.Обчислити наступні інтеграли методом прямокутників та методом трапецій. Порівняти отримані значення із значеннями знайденими аналітично. Розрахувати похибку при використанні кожного з методів.

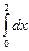
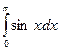
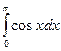
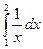
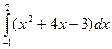
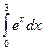
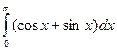
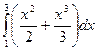
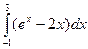
Дата добавления: 2014-11-29