Построение прямой, проходящей через две заданные точки

CreateSpace(F, t0, t1, tgrid, tmap)

Применение новой функции CreateSpace

Matchad 2000 имеет еще одну новую графическую функцию:

Эта функция отличается oт функции CreateMesh только тем, что заданная в век­торном виде функция F задается как функция одной переменной tgrid, причем параметры t0 и t1 устанавливают пределы ее изменения, a tmap - число линий сетки. Для построения графика используется шаблон типа Scatter Plot (шаблон для графика в виде точек (фигур) в трехмерном пространстве). С помощью этой функции удобно строить точечные трехмерные графики в виде пространственных спиралей и иных подобных геометрических образов.

Функция одной переменной F задается в векторной форме, затем определяются пределы изменения переменной и число точек графика tgrid. Число линий сетки можно не задавать. Пример использования функции CreateSpace приведен на рис.8.26.

Рисунок 8.26 - Пример использования функции CreateSpace

8.5 ПОСТРОЕНИЕ ГРАФИКОВ ПО РЕЗУЛЬТАТАМ МАТЕМАТИЧЕСКИХ ВЫЧИСЛЕНИЙ

Даны две точки A (x1, y1) и B(x2, y2). Задано x1=-1, y1=-1, x2=1, y2=1. Через эти точки надо провести прямую линию и найти расстояние между ними.

Уравнение прямой может быть записано так:

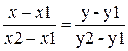
Угловой коэффициент определяется формулой:

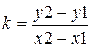
Уравнение можно записать:

Расстояние между двумя точками вычисляется по формуле:

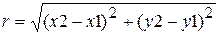
На рис.8.27 приведено решение этой задачи в системе Mathcad. Обратите внимание на форматирование графика и использование текстового блока для того, чтобы пометить точку A и B.

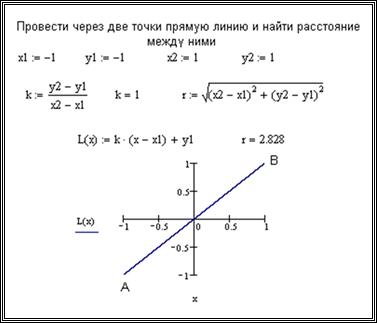
Рисунок 8.27 - График прямой, проходящей через две заданные точки

8.5.2 Построение графика функции y = f(x), графика первой и второй производной этой функции

Найти производную первого и второго порядка функции y = f(x) и на одном графике построить график функции y = f(x), график первой и второй производной этой функции. Решение этой задачи приведено на рис.8.28.

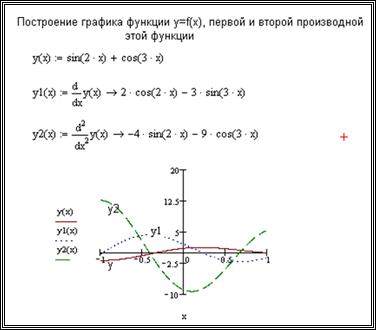
Рисунок 8.28 - График функции y = f(x), первой и второй производной этой функции

8.5.3. Построение графика касательной и нормали к кривой y = f(x)

Надо построить график касательной и нормали к кривой y = f(x) в точке с абсциссой a. Для этого необходимо найти первую производную функции y = f(x).

Если функция y = f(x) в точке a имеет конечную производную, то уравнение касательной имеет вид:

.

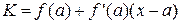Если f’(a) = ¥, то уравнение касательной имеет вид: x = a.

Если f’(a) ¹ 0, то уравнение нормали имеет вид:

.

Если f’(a) = 0, то уравнение нормали имеет вид: x = a.

Пример решения данной задачи приведен на рис.8.29. Для правильного представления нормали масштабы по осям должны быть равны.

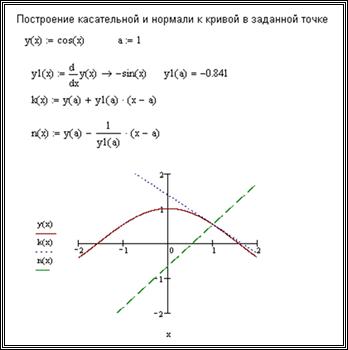
Рисунок 8.29 - График касательной и нормали к кривой в заданной точке

Дата добавления: 2014-11-29