Тема 4. Нелінійні оптимізаційні моделі економічних систем

Контрольні запитання

1. Які методи існують при вирішенні задач лінійного програмування?

2. Сформулюйте економічну постановку задачі розрахунку оптимальної виробничої програми підприємства.

3. Побудуйте математичну модель задачі оптимальної виробничої програми.

4. Що в задачі оптимального випуску продукції визначає цільова функція?

5. Що в задачі оптимального випуску продукції визначають обмеження на змінні?

6. Що в задачі оптимального випуску продукції визначають умови невід'ємності змінних?

7. Який план вважається оптимальним на підприємстві?

8. Записати економіко-математичну модель задачі оптимального розподілу завдань з випуску однорідної продукції.

9. Наведіть порядок визначення оптимальної виробничої програми підприємства із застосуванням електронних таблиць Excel.

10.Пояснити суть транспортної задачі.

11.Записати економіко-математичну модель транспортної задачі.

12.Яка модель транспортної задачі називається закритою?

13.Яка модель транспортної задачі називається відкритою?

14.Назвіть методи реалізації транспортної задачі.

15.Наведіть порядок рішення транспортної задачі із застосуванням електронних таблиць Excel

Література: [1, с. 354-377, 385-392, 436-455; 2, с. 69-72, 117-190; 6, с. 120-137; 7, с. 102-128, 251; 9, с. 45-58, 53-54, 59, 63-65; 13, с. 9-11, 31-39, 41-47, 60-63, 75-87].

Взаємозв’язки між економічними показниками досить часто носять нелінійний характер і побудована лінійна модель в такому випадку буде неадекватна реальній дійсності. Нелінійне програмування використовується для задач планування виробництва, управління ресурсами, контролю якості продукції.

В загальному випадку задача нелінійного програмування має вигляд:

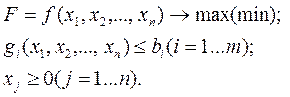(4.1)

де 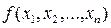, 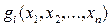– нелінійні залежності цільової функції та обмежень.

Для розв’язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів та обчислювальних алгоритмів, які в основному ґрунтуються на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі.

До нелінійних методів знаходження оптимізаційних рішень відносяться: класичний метод оптимізації (за допомогою множників Лагранжа); метод прямого пошуку (градієнтний метод); випукле (квадратичне) програмування; метод Куна-Такера, та ін.

Часто задачу нелінійного програмування намагаються привести до лінійного виду, але заміна функції призводить до значних похибок, що зображено на рис. 4.1.

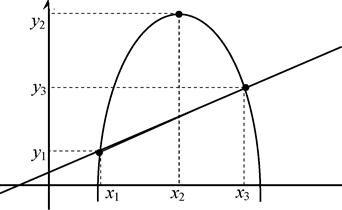
Рис. 4.1. Приклад випуклої функції.

В точках х₁ та х₃ значення обох функцій співпадають, а в точці х₂ відрізняються значною мірою.

Ми бачимо, що лінеаризація нелінійних процесів не завжди себе виправдовує і в загальному випадку є досить складною математичною задачею.

При розв’язуванні нелінійних задач використовують наближені методи, більшість яких дають змогу знаходити локальні оптимуми, а вже знайшовши всі локальні оптимуми, методом порівняння значень цільової функції у кожній з точок локального оптимуму можна знайти глобальний. Наприклад, на рис. 4.2 маємо на деякому відрізку локальні оптимуми в точках х ₁, х ₂, х ₄, х ₅, х ₆, х ₇, х ₉ та х ₁₀, а глобальні – в точках х ₃ та х ₈. Проте для практичних розрахунків такий метод не завжди ефективний, тому що часто наближені методи не «вловлюють» глобального оптимуму, особливо коли глобальний оптимум лежить досить близько до локального.

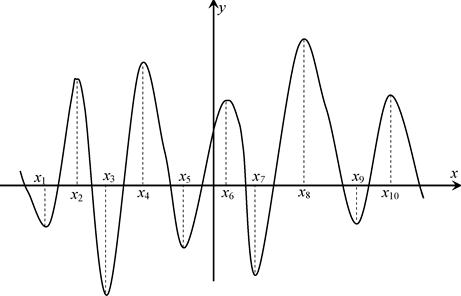
Рис. 4.2. Приклад нелінійної функції.

У задачах лінійного програмування точка оптимуму завжди була граничною, а в нелінійних вона може бути або граничною, або такою, що міститься всередині допустимої області розв’язків.

Дата добавления: 2014-11-29